Определение кинематических параметров прямолинейно-огибающего механизма по заданным размерам рабочего пространства на примере пресса для утилизации кузовов автомобилей

Введение. Механизм называется прямолинейно-огибающим, если у его исполнительного органа рабочая поверхность образована дугой окружности, а движется он по сложной траектории, огибая поверхность, образованную прямой, то есть прямолинейную. На рис. 1 показан кривошипно-кулисный прямолинейно-огибающий механизм, состоящий из ведущего кривошипа 1, шарнирно связанного с кулисой 2, которая подвижно соединена с качающимся ползуном 3, установленным на стойке, и с которой жёстко связан рабочий орган 4, образованный дугой окружности радиуса R, центр кривизны которой расположен в направляющей точке М. Во время вращения приводного кривошипа 1 дуга окружности, жёстко связанная с кулисой 2, совершает движение огибания относительно неподвижной прямой, образующей прямолинейную поверхность основания (стойки) 5, по принципу «пресс-папье». В этот момент центр кривизны дуги — направляющая точка М движется приближённо по прямолинейной траектории параллельно огибаемой прямой, что соответствует рабочему ходу механизма. При дальнейшем вращении кривошипа рабочий орган, образованный дугой окружности, отрывается от огибаемой прямой и переносится в исходное положение, а точка М движется по криволинейной траектории, что соответствует холостому ходу механизма.

Приближённые прямолинейно-огибающие механизмы имеют широкие перспективы применения в различных областях техники [1]. В частности, использование таких механизмов для обработки материалов давлением сулит существенное снижение энергопотребления и материалоёмкости оборудования. Прессы на их основе просты по конструкции, используют принцип локального нагружения обрабатываемых материалов и обладают высокой передаточной функцией в сравнении с любыми другими прессами с простым поступательным движением пуансона.

За рубежом неоднократно проводились исследования, направленные на решение задач синтеза таких механизмов. При этом приближённое воспроизведение траектории точки или плоского движения тела чаще всего обеспечивается оптимизацией методом Монте-Карло [2] или методом Ньютона — Рафсона [3].

Работа выполнена в рамках инициативной НИР.

Рис. 1. Прямолинейно-огибающий механизм пресса для утилизации автомобилей

В работе [4] решается задача минимизации погрешности воспроизведения заданной траектории движения точкой на шатуне четырёхзвенного рычажного механизма. Траектория задаётся точками. Не налагаются ограничения на степень её дискретизации. Вводится критерий оптимизации (целевая функция) — максимальное отклонение А направляющей точки от заданной траектории. Это отношение минимизируется при условии, что соблюдаются необходимые соотношения между размерами звеньев. Данная задача оптимизации решается методами нелинейного программирования. Задача синтеза четырёхзвенного стержневого механизма со сферическими парами в работе [5] решается применением метода минимальных квадратов. При этом траектория выходного звена — кривая, заданная в точках. От угла поворота звеньев зависит погрешность, определяемая как разница координат точки выходного звена и координат точек, заданных на траектории. Задача сводится к решению численным методом системы нелинейных уравнений.

Решение задачи синтеза прямолинейно-направляющих механизмов методом оптимизации предполагает произвольный выбор первой комбинации искомых параметров синтеза, поэтому требует достаточно большого объёма вычислений. В этой связи наилучшим можно считать комбинированный метод, сочетающий достоинства методов оптимизации и интерполяции. Начальное интерполяционное приближение функции по трём узлам интерполирования, расположенным по концам отрезка приближения и в середине его, позволяет значительно сократить число итераций при минимизации вспомогательной целевой функции.

Результатом обобщения различных методик и системного подхода к пониманию синтеза прямолинейно-направляющих механизмов является работа [1]. Её авторы на основе интерполяционного метода приближения функции разработали приближённый синтез симметричных пря-молинейно-огибающих механизмов. Установлено, что синтез механизма со сложным прямолиней-но-огибающим движением рабочего органа сводится к интерполяционному синтезу механизма, направляющего центр кривизны огибающей дуги по прямой линии, параллельно заданной. При этом используется метод интерполяционного приближения траектории центра кривизны дуги с учётом скольжения между взаимоогибаемыми кривыми [1].

Положение направляющей точки М определяется суммой векторов г_х и г₂. Причём длина вектора г_х равна длине кривошипа, а длина вектора г₂ есть расстояние между точкой сочленения кривошипа и шатуна и направляющей точкой М. Положение векторов г_х и г_г определяется углами ф_т и ф2, откладываемыми от оси ординат. Длина огибаемого участка прямой равна длине прямолинейного участка траектории движения точки М вдоль оси ординат:

L = 2(г151Пф1 + Г251Пф2),(1)

где ф2 — функция поворота шатунной плоскости от обобщённой координаты ф2 = ф2 (ф^.

Длина огибающего отрезка дуги:

/ = /?-2ф = /?-2(п-ф2).(2)

Условие равенства ординат направляющей точки М в середине и конце интервала приближения является условием синтеза прямолинейно-направляющего и прямолинейно-огибающего механизма и называется уравнением схемы в общем виде:

Д = Гх СО5ф° + Г, СО5ф2 - Гх СО5ф1 - Г, СО5ф2 = 0 , где ф° — угол поворота кривошипа, соответствующий середине интервала приближения; ф2 — значение функции положения шатунной плоскости в середине интервала приближения при ф°; Ф1 — угол поворота кривошипа, соответствующий концу интервала приближения; ф2 — функция положения шатунной плоскости в конце интервала приближения.

Скольжение представляет собой разность между перемещением точки М на расстояние L (длина интервала приближения) и длиной огибающей дуги /за это же время:

Е = L - / = 2 (г; sin ф_х + г₂ sin ф₂ - R (п - ф₂)).                          (4)

В общем случае синтез прямолинейно-огибающих механизмов сводится к решению системы нелинейных уравнений (1) — (4), которые являются общими для всех прямолинейно-огибающих механизмов [6-8] и позволяют определять их параметры. С этой целью в качестве параметра ф2 подставляется выражение для соответствующей функции поворота шатунной плоскости (зависит от вида направляющего механизма). Например, для кривошипно-кулисного механизма, показанного на рис. 1, функция поворота шатунной плоскости имеет вид:

Ф2 = п + arcsm .      1     1 г,                               (5)

+ b² + lr_xb cos ф!

где Ь — расстояние между осями вращения кривошипа и качающегося ползуна.

Для наилучшего приближения к прямой линии количество узлов интерполяции на интервале приближения должно равняться порядку шатунной кривой. Наилучшее приближение обеспечивает максимально возможную точность воспроизведения заданной кривой при минимально возможных размерах звеньев механизма. При этом приближение считается равномерным, если все максимальные отклонения заменяющей кривой по обе стороны от заданной прямой одинаковы [1].

В данном случае уравнение схемы (3) соответствует не наилучшему, а так называемому промежуточному приближению, поскольку шатунная кривая кривошипно-кулисного механизма является кривой шестого порядка, а интерполяционных узлов на интервале приближения предусмотрено только три — в середине интервала приближения и на его концах. Впрочем, практика показывает, что наилучшее приближение незначительно отличается от промежуточного и проявляется в увеличении длины интервала приближения, но использование промежуточного приближения значительно упрощает расчёт.

Входными параметрами синтеза являются: длина интервала приближения L, скольжение £ между взаимоогибаемыми дугами окружности и прямой, отклонение Д траектории направляющей точки и угол поворота кривошипа ф_х. Неизвестные параметры — г_х, г_г, b, R и /.

Если произвести подстановку функции положения ф₂ в систему уравнений (1) — (4), можно показать, что представленная система уравнений нелинейна относительно неизвестных параметров. В этом случае задаются параметрами механизма (например, г_х и /?) из конструктивных соображений, обусловленных допустимыми размерами устройства. Либо система решается методом оптимизации. Кроме того, необходима адаптация метода к заданным параметрам технологического процесса, например к размерам обрабатываемой заготовки или получаемого изделия.

Цели данного исследования:

• -    формализация зависимостей между параметрами прямолинейно-огибающего механизма на базе метода интерполяционного приближения функций;

• -    адаптация полученной методики к решению задачи синтеза обжимного пресса для утилизации кузовов автомобилей (исходя из заданных параметров рабочего штамповочного пространства, определяемого конкретными размерами кузова);

• -    оценка точностных характеристик процесса.

Основная часть. Для решения поставленных задач определим параметры рабочего пространства обжимного пресса. Эти параметры послужат исходными данными для кинематического синтеза прямолинейно-огибающего механизма пресса, работа которого связана с деформацией обрабатываемого изделия. К ним относятся: Н — максимальная высота рабочего пространства пресса (определена максимальной габаритной величиной обрабатываемого изделия); h — высота получаемого после обработки изделия; о' — угол раскрытия рабочего органа прямолинейно-огибающего механизма; L — длина рабочего пространства механизма, равная длине интервала приближения.

Если принять, что угол раскрытия рабочего органа обжимного пресса о' = ф, функцию по ворота шатунной плоскости механизма, соответствующей положению рабочего органа вначале рабочего хода, можно представить в виде:

,       H-h

ф2=п + ф = п + о= п + arctg—-—

Отклонение Д траектории направляющей точки М от прямой линии на заданном интервале, определяемое как разность между ординатой точки М в начале интервала приближения и текущей ординатой, должно быть минимальным. Тогда функцию отклонения (3) с учётом функции Ф₂ положения шатунной кривой механизма по уравнению (6) можно представить в виде:

Д = (1 - созф^ - г2 (1 + созф2) = 0.

Приравняв отклонение к нулю, определяем параметр г₂ — расстояние от точки В до направляющей точки М из условия промежуточного приближения:

_г /1(1 -«кф,)

2    1+СО5ф2 "

С учётом функции ф2 по уравнению (6) получим

_ гДХ-созф^

• ² 1 + СО5(п + ф)"

Из уравнения (1), определяющего длину прямолинейного участка траектории движения точки М, находим длину кривошипа ri, подставив в него уравнение (8):

Д(1-СО5ф)

г = ______________1_______22_____________.

1 2з1Пф1 (1 — СО5ф) — 2з1пф(1 — СОЗф^ "

По теореме синусов из ВАВСсоставим соотношение: Д b sinqj зю^-ф)'

отсюда длина стойки:

^ г^п^-ф) sinqi

(Ю)

Движение огибания дугой окружности неподвижной прямой сопровождается скольжением £, которое вызывает силы трения в контактной паре «дуга — прямая». Это увеличивает нагрузку на привод и снижает стойкость инструмента, поэтому синтез механизма проводится из условия минимального скольжения на интервале приближения [9]. Скольжение равно нулю, если равна нулю разность между перемещением точки М на расстояние L и перемещением за это же время огибающей дуги длиной /, то есть:

£=£-/=0,                          (И)

где / — длина дуги, образующей поверхность рабочего органа.

/ = 2Яф.

Подставив функции для L и / в уравнение (И), определим радиус дуги окружности из условия нулевого суммарного скольжения:

r_x sin ф! + г₂ sin (п + ф) = 2/?ф.

Тогда величина радиуса дуги окружности:

г. зюф. + г, sinfn + ф) l

_ 1 _____ ^Т1 2 ____\____ ^т / _

2ф

2ф

Однако это не означает, что скольжение равно нулю в любой момент времени. Из уравнения следует, что скольжение равно нулю только в интерполяционных узлах, то есть в точках, где траектория направляющей точки М — центра кривизны дуги пересекает либо касается прямолинейной траектории, параллельной огибаемой прямой.

Таким образом, решая совместно уравнения (8) — (10), (12), определяем все параметры прямолинейно-огибающего механизма. Для решения данных уравнений необходимо угол ф подставить в виде соотношения параметров рабочего штамповочного пространства из уравнения (6), которые задаются из технологических условий.

После того как найдены параметры механизма, определяются значения функции отклонения Д и скольжения £ на расчётном интервале приближения L от заданного угла поворота кри- вошипа ф!:

Д = Г1(1-СО5ф1)-Г2(1+СО5ф2).                         (13)

£ = 2(г1з!пф1 +Г25Юф2-/?(п-ф2)).                        (14)

Таким образом можно оценить точность воспроизведения закона движения и соответствие полученной схемы механизма заданной точности технологического процесса. При определении отклонения Л и скольжения £ функцию положения следует представить через найденные параметры механизма в соответствии с уравнением (5). Это позволит получить функции на всём интервале приближения и определить экстремумы функции через дифференцирование по обобщённой координате фх.

Рассмотрим, как работает модель определения параметров, на примере прямолинейно-огибающего механизма пресса для утилизации кузова автомобиля (см. рис. 1).

Синтез начинается с определения технологических параметров рабочего штамповочного пространства. На рис. 2 представлен план кузова автомобиля ВАЗ-2121, геометрия которого характеризуется следующими параметрами: о — угол подъёма кузова, град; L_a — габаритная длина кузова, мм; h_k — высота капотного пространства, мм; Н_а — габаритная высота кузова автомобиля, мм; Ь_а — габаритная ширина кузова.

При утилизации автомобиля с помощью пресса со сложным огибающим движением исполнительного органа кузов размещается между взаимоогибаемыми выпуклым рабочим органом 4 и плоским основанием станины 5 (см. рис. 1) и подвергается деформации до заданной высоты брикета h_6p . Таким образом, огибаемая прямая будет расположена на высоте h_6p от основания пресса параллельно её поверхности. При известном угле подъёма кузова о определяем длину рабочего штамповочного пространства, равную длине интервала приближения:

tgo

Угол раскрытия рабочего органа механизма обжимного пресса:

а' = arctg

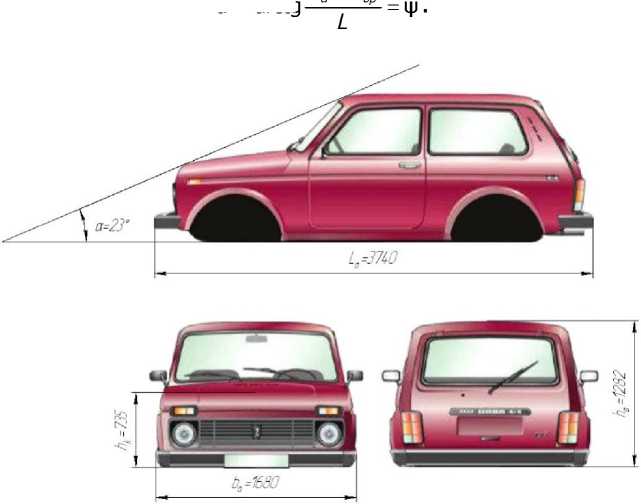
Рис. 2. Геометрия кузова легкового автомобиля ВАЗ-2121

Таким образом, зная параметры кузова автомобиля На, о, а также высоту брикета, которую требуется получить на выходе с линии прессования, можно определить параметры рабочего пространства обжимного пресса и все параметры схемы механизма. Задавшись величиной угла поворота кривошипа cpt, соответствующей положению механизма в начале рабочего хода или в начале интервала приближения (на схеме фх = 90°, то есть рабочий ход составляет 180°), определяем следующие величины.

• 1)    Длина штамповочного пространства пресса:

1 'ЭО'Э

L = s- =----= 3032 мм, tgo tg23° где На = 1282 — габаритная высота кузова автомобиля ВАЗ-2121, мм; о = 23° — угол подъёма кузова автомобиля ВАЗ-2121.

• 2)    Угол раскрытия рабочего органа пресса:

,         Ha"h6P .1282-350 „ э а = ш = arctq ——— = arctq--------= 0,3 рад.

L            3032

• 3)    Длина кривошипа приводного механизма обжимного пресса (9):

3032(1-cos 0,3)

л =-------7-------Ц-------Ц---------7 = 270 мм.

2 sin 1,57 (1 - cos 0,3) - 2 sin 0,3 (1 - cos 1,57)

• 4)    Расстояние от точки В до направляющей точки М(7):

t\ (1 - cos ф_х)   270 (1 - cos 1,57)

= 6079 мм.

2 1 + СО5(п + ф)

l-cos0,3

• 5)    Длина стойки приводного механизма обжимного пресса (10):

  Ь =

  
  

  г_т si п (ф_т - щ) 270 sin (1,57 - 0,3)

  
  

  з!пф

  
  

  sin (0,3)

  
  

  = 873 мм.

  
  

• 6)    Радиус дуги окружности, образующей поверхность рабочего органа обжимного пресса:

L 3032

R =            = 5053 мм.

2ф 2-0,3

Для разработанной модели составлена программа автоматизированного расчёта параметров прямолинейно-огибающего механизма в математической среде Maple. Результаты расчётов параметров механизма обжимного пресса в среде Maple представлены на рис. 3 и 4 в виде графиков зависимостей отклонения A-f^J и скольжения £ = Г(ф1) на интервале приближения, соответствующего рабочему ходу механизма.

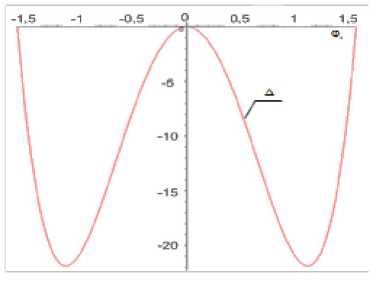
Рис. 3. Г рафик отклонения Д, мм на интервале приближения при cpi от -п/2 до п/2

На графиках ось абсцисс представляет собой мнимую огибаемую прямую, которая разбита в диапазоне изменения угла поворота кривошипа рабочего хода механизма. Ось ординат представляет собой осевую линию симметрии, делящую интервал приближения и шатунную кривую на равные полуинтервалы. Угол рабочего хода механизма пресса равен 180° (на графике — от -п/2 до п/2).

Анализ графиков показывает, что функция отклонения достигает максимального значения А = 22 мм на всём интервале приближения, равном длине штамповочного пространства обжимного пресса (причём первый раз на отрицательном полуинтервале, второй раз — на положительном). Относительно мнимой огибаемой прямой траектория точки контакта отклоняется в направлении деформации, то есть минимальная высота полученного после деформации брикета будет на 22 мм меньше.

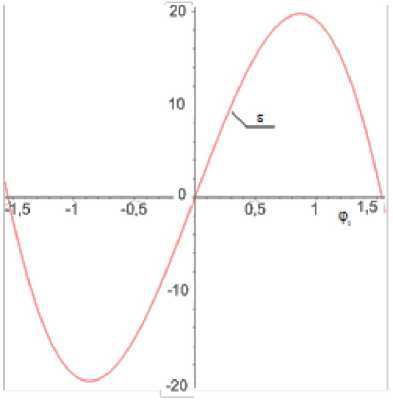
Рис. 4. Г рафик скольжения г, мм на интервале приближения при cpi от -п/2 до п/2

Скольжение принимает максимальные значения 19 мм. Из графика видно, что на отрицательном полуинтервале присутствует скольжение «назад» (соответствует кривой, расположенной в отрицательной области графика), а на положительном полуинтервале — скольжение «вперёд» [10]. Интегрально же величина скольжения равна нулю.

Выводы.

• 1.    Описанная методика позволяет определять кинематические параметры обжимного пресса для утилизации кузовов автомобилей. По габаритам такой пресс оказывается значительно меньше других прессов, выполняющих данную операцию. Это предопределяет перспективы его применения с учётом актуальности утилизации и вторичной переработки кузовов.

• 2.    Как следует из приведённого примера, параметры точности обжатия и скольжения не оказывают решающего влияния на результаты данного технологического процесса, поэтому могут варьироваться в достаточно значительных пределах.