Определение коэффициента интенсивности напряжений первого типа для двух коллинеарных неоднородных трещин методом граничных элементов

Отсутствие математических моделей, описывающих рассматриваемый процесс численными методами, а также предоставление возможности для использования полученных результатов в области механики разрушения, обуславливают актуальность данной статьи.

Цель исследования

Целью данной статьи является разработка алгоритма численного расчета коэффициента интенсивности напряжений (далее КИН) первого типа для двух коллинеарных трещин, обладающих отличиями в механических свойствах, с помощью метода граничных элементов.

Постановка задачи

В статье рассматривается случай совместного раскрытия двух коллинеарных трещин равной длины L, расположенных на расстоянии b друг от друга (рис. 1). Особенностью рассматриваемого случая является наличие материала-заполнителя в полости второй трещины, характеризуемого некоторым значением модуля Юнга E*, отличного по значению от модуля окружающей сплошной среды E. Под действием внутреннего давления рвн в левой трещине, деформированное состояние среды, описываемое непрерывными аналитическими функциями, претерпевает разрывы в окрестностях рассматриваемых трещин. Смещение противолежащих берегов трещины относительно друг друга представляет собой разрыв смещений в данной точке при определении деформированного состояния среды.

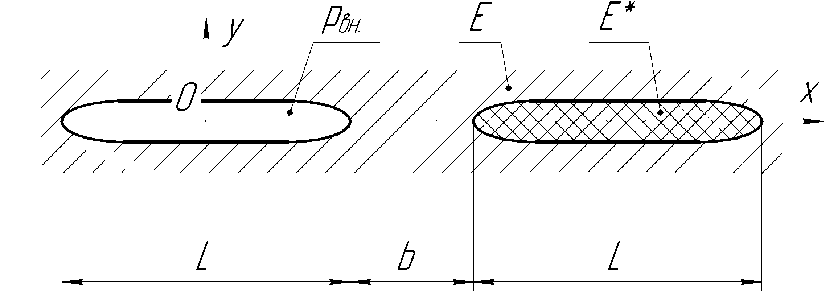
Рис. 1. Расчетная схема

В рамках данной статьи рассматриваются серия численных экспериментов, направленных на анализ напряженно-деформированного состояния трещин, которая производится исходя из следующих принятых исходных данных:

• 1)    Длина трещины L =5П0^-3 м;

• 2)    Число граничных элементов на одной трещине N =100 шт.;

• 3)    Коэффициент Пуассона v =0,25;

• 4)    Внутреннее давление р вн =100^10 6 Па.

• 5)    Ширина промежутка между трещинами b =1-10^-3 м;

• 6)    Модуль Юнга основного материала E =340¹⁰ Па;

• 7)    Модуль     Юнга     материала-

• заполнителя второй трещины

( 0 \ 0,25 0,50 I 0,75 1,00/

Е =

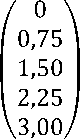
• 1010Па

• 8)    Толщина слоя материала заполнителя К зап. = 10 ³ м

Методика расчета

В рамках данной статьи рассматривается численный метод расчета - метод граничных элементов. Подробное описание методики численного расчета разрывов смещений приведено в [1].

Расчет разрывов смещений

Определение разрывов смещений в трещинах по принятой расчетной схеме (см. рис. 1) производится аналогично методике рассмотренной в [2].

Результаты расчета приведены на графике 1. Из соображений симметрии расчетной схемы на графике приведены половины величин раскрытия трещин.

Рис. 2. Раскрытие трещин

Анализируя полученные значения можно прийти к выводу о том, что по мере уменьшения величины модуля Юнга материала-заполнителя ( E* ) величина раскрытия второй трещины возрастает.

Определение коэффициента интенсивности напряжений

В рамках данной статьи КИН первого типа для системы из двух равнонагружен-ных трещин определялся на основе полученных значений разрывов смещений

K =

pf Е р ^ ^32(1 —и2)!™ 77—^

где l – половина длины трещины, м;

x – продольная координата с началом отсчета в центре трещины, м.

Для получения сравнительных характеристик с известными аналитическими моделями необходимо представить полученные значения разрывов смещений в аналитическом виде

М4нчт), где V(x) – вспомогательная функция, определяемая как

4(1 — w2)     /-------

V(x) =V      ' pBH^ I2 — X2

E

/ (у) - регрессионное уравнение, определяемое как

Е *\              Е *        /Е *\²        /Е *\³        /Е *\⁴

/"Ы^о + ^у + Цу) +аз(-) +а4(-)

где a 0 , a 1 , a 2 , a 3 , a 4 – неизвестные коэффициенты регрессии.

Используя метод наименьших квадратов (МНК) и полученные значения разры- вов смещений были получены значения коэффициентов регрессии, соответствующие выражению (5). Результаты приведены в таблице 3.

Таблица 3. Коэффициенты регрессии

Коэффициент регрессии	Значение, 10-5
a 0	1,21
a 1	-0,55
a 2	1,34
a 3	-1,44
a 4	0,56

Т.о., преобразовывая (2) подстановкой (3-5) можно получить выражение для коэффициента интенсивности напряжений в зависимости от степени неоднородности трещин (отношение —) расчетной схемы

Ez

K i

^p‘" j”z ('

«0 + а1 Т" + ^2 Е

(т)2

+ аз

е3

+ ^4

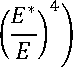
Анализ полученных результатов

Результаты, полученные с использова- приведены на графике 2. нием определенной регрессионной кривой

Рис. 3. Зависимость КИН от степени неоднородности трещин

Исходя из полученных результатов модно сделать вывод о том, что по мере упрочнения материала-заполнителя по сравнению с окружающей средой значение КИН уменьшается, что свидетельствует о меньшей величине раскрытия трещин.

Выводы

• 1.    В настоящей статье разработана численная математическая модель (6) описы-

• однородных трещин, одна из которых нагружена внутренним давлением.

• 2.    Для конкретных исходных данных представлены значения разрывов смещений (см. график 1).

• 3.    В результате расчета, основанного на методике, представленной в работе [2] получены результаты, обладающие научной новизной ввиду отсутствия сравнительных аналогов аналитического и численного ха-

• вающая раскрытие двух коллинеарных не- рактера.