Определение коэффициента интенсивности напряжений первого типа массива трещин

Отсутствие аналогов численных и аналитических решений описывающих рассматриваемую систему трещин обуславливают актуальность данной статьи.

Цель выполненного исследования является разработка алгоритма численного расчета коэффициента интенсивности напряжений (далее КИН) первого типа для системы плоских трещин.

Постановка задачи

В статье рассматривается случай раскрытия массива плоских трещин равной длины L (см. рис. 1), образованного совокупностью из восемнадцати правильных шестигранников, диаметр описанной окружности которых равен 2L. Под действием внутреннего давления p, воздействующего на центральную трещину, деформированное состояние среды, описываемое непрерывными аналитическими функциями, претерпевает разрыв в окрестности рассматриваемой трещины. Смещение противолежащих берегов трещины относительно друг друга представляет собой разрыв смещений в данной точке при определении деформированного состояния среды.

2L

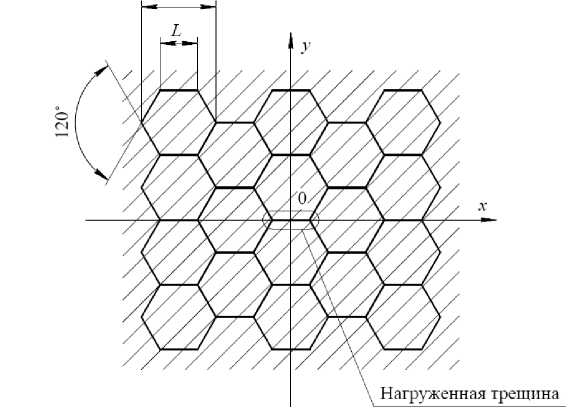
Рис. 1. Расчетная схема

В рамках данной статьи рассматривается серия численных экспериментов, направленных на анализ напряженно-деформированного состояния центральной трещины. Расчеты производятся исходя из следующих принятых исходных данных:

• 1)    коэффициент Пуассона v =0,25;

• 2)    модуль Юнга материала E =3-10¹⁰ Па.

Методика расчета

В данной статье применяется численный метод расчета - метод граничных элементов. Подробное описание методики численного расчета разрывов смещений приведено в [1].

Расчет разрывов смещений

Определение разрывов смещений в трещинах по принятой расчетной схеме (см. рис. 1) производится аналогично методике рассмотренной в [2].

Применяя данную методику к текущей расчетной схеме (см. рис. 1) возможно получить значения разрывов смещений для всех граничных элементов трещин. На рисунке 2 приведено изображение данных разрывов в центральной трещине, находящейся под нагрузкой.

Разр ний,

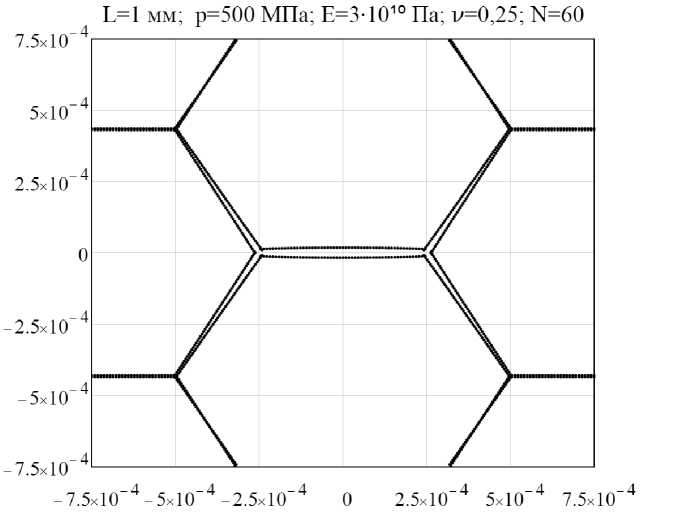
Координата x , м

Рис. 2. Разрывы смещения центральной трещины

Определение коэффициента интенсивности напряжений

В рамках данной статьи КИН первого типа для рассматриваемого массива трещин определялся исходя из наибольшего значения среди всех трещин массива. Данной трещиной является центральная трещина (см. рис. 1). На основе полученных значений разрывов смещений КИН определяется согласно выражению

« 1 =

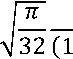
Е     Dn

-“2)Л-^

где L - длина трещины, м;

D n - разрыв смещения в N -ом граничном элементе трещины;

• x n    - координат центра N -го граничного элемента, м;

N - число граничных элементов одной трещины, принятое равным 40.

В ходе расчетов были следующие расчетные интервалы длин трещин и давлений нагружающих центральную трещину:

L=[0,5; 1,0;. 5,0] мм(2)

p = [100;200;.500]МПа(з)

Результаты расчета приведены в таблице 1.

Таблица 1. Значения КИН

Длина трещины L , мм	КИН первого типа при давлении p , 107^Па Тм
	p =100 МПа	p =200 МПа	p =300 МПа	p =400 МПа	p =500 МПа
0,5	2,04	4,07	6,11	8,14	10,18
1,0	2,88	5,76	8,64	11,51	14,39
1,5	3,53	7,05	10,58	14,10	17,63
2,0	4,07	8,14	12,12	16,28	20,35
2,5	4,55	9,10	13,65	18,21	22,76
3,0	4,99	9,97	14,96	19,94	24,93
3,5	5,39	10,77	16,16	21,54	26,93
4,0	5,76	11,51	17,27	23,03	28,79
4,5	6,11	12,21	18,32	24,43	30,53
5,0	6,44	12,87	19,31	25,75	32,18

Для описания полученных значений КИН в аналитической форме было выбрано выражение, соответствующее виду

^(u,^) = pAL5 + C ,(4)

где A , B , C – постоянные коэффициенты;

С помощью функции Minerr в среде Mathcad 15, позволяющей определить численное решение системы уравнений методом секущих были определены неизвест- ные коэффициенты уравнения (4). Результаты приведены в таблице 2. Семейство кривых, построенное совместно, со значениями, полученными в ходе численного расчета (см. табл. 1) приведено на рисунке 3.

Таблица 2. Значения коэффициентов

Коэффициент	A	B	C
Значение	9,1	0,5	1,27 Па Тм

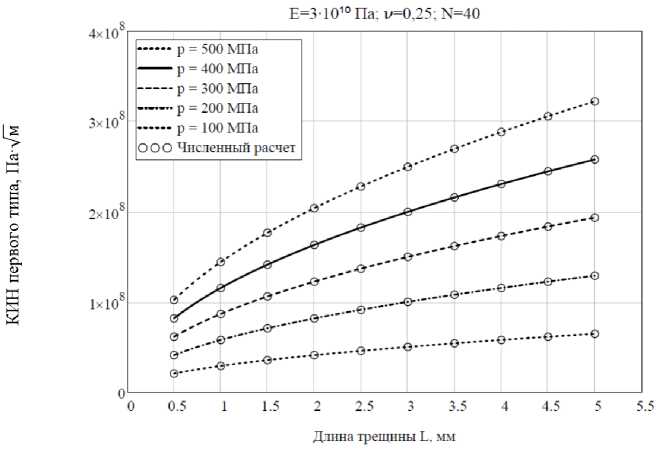
Рис. 3. Значения КИН

Анализ полученных результатов

Для сравнения полученного численного решения и подобранного аналитического выражения в каждой расчетной точке была определена относительная погрешность расчета

|^ чм - ^ ан | ^ чм

где Кчм – значение КИН полученное      Результаты определения максимальных численным методом (см. рис. 1);             значений относительных погрешностей

К ан – значение КИН согласно выраже- приведены в таблица 3.

нию (4).

Таблица 3. Значения максимальных относительных погрешностей

Давление p , МПа	100	200	300	400	500
Максимальная погрешность δ max , %	0,03	0,05	0,04	0,05	0,09

Выводы

• 1.    В настоящей статье представлен способ определения КИН первого типа для массива трещин, с центральной трещиной нагруженной внутренним давлением (см. рис. 1).

• 2.    Получено аналитическое выражение (4) соответствующее численному решению, которое основывается на известной аналитической модели [2-4].