Определение коэффициента теплопередачи грунтового массива в процессе зимнего бетонирования

Точная оценка температурно-прочностных параметров зимнего бетонирования – залог обеспечения качества монолитных железобетонных конструкций, а также путь к минимизации расходов энергии на их термообработку [1, 2].

Существующие методы расчета параметров зимнего бетонирования основаны на использовании приведенного коэффициента теплопередачи ограждения твердеющего бетона [3–7], который характеризует величину его теплопотерь в окружающую среду. Приведенный коэффициент является интегральной величиной, учитывающей коэффициенты теплопередачи различных материалов, соприкасающихся с бетоном. Определение коэффициента теплопередачи таких конструкций, как опалубка и утеплитель, не вызывает трудностей в виду ограниченной их толщины [3–10]. В то же время для таких конструкций, как фундаменты, определение коэффициента теплопередачи грунта по известным методикам невозможны в виду бесконечности толщины поперечного сечения грунта.

Отметим, что процесс распространения тепла в грунтовом массиве не описывается классической для строительной науки теорией теплопроводности, как, например, процесс теплопередачи от более нагретой среды к менее нагретой через разде- ляющую их стенку определенной толщины и из определенного материала. Для решения задачи применительно к грунту необходимо использовать также приёмы математической физики и теории решения дифференциальных уравнений.

Сформулируем задачу. На поверхность грунтового основания укладывается бетонная смесь с определенной начальной температурой и выдерживается в течение определенного времени. Примем, что бетонная смесь выдерживается с постоянной температурой, равной её начальной. Грунтовое основание отогретое (или имеет положительную температуру благодаря выполненным мероприятиям по защите от промерзания) имеет одинаковую, равномерно распределенную температуру на достаточную глубину (не менее 3–4 метров). Необходимо получить аналитическую зависимость, описывающую процесс теплопередачи выдерживаемого бетона грунтовому основанию.

Как и любая задача теплопроводности, данная задача решается через дифференциальное уравнение теплопроводности [11, 12]. Представим массив грунтового основания в виде полуограниченного тела (ограниченное с одной стороны плоскостью yz , а с другой стороны – в направлении оси x – простирающееся в бесконечность).

Технология и организация строительного производства

В соответствии с описанной ситуацией при-

мем начальные условия распределение температуры внутри грунтового массива.

Температура полуограниченного тела (массива грунтового основания) во всех точках имеет постоянное значение: T ( x ,0 ) = const.

Выдерживание бетонной смеси на поверхности грунтового основания с постоянной температурой соответствует граничному условию первого рода (задание температуры поверхности полуогра-ниченного тела).

Таким образом, в начальный момент времени ( t = 0 ) поверхность полуограниченного тела принимает температуру T _c (температура уложенной бетонной смеси), которая затем поддерживается постоянной в течение времени выдерживания бетонной смеси т.,,,,.

выдерж

меним метод интегрального преобразования Лапласа , поскольку данный метод наиболее эффективно использовать по временной координате, а также по пространственной координате для тел, имеющих полуограниченную протяженность [13].

Суть преобразования Лапласа в том, что изучается не сама функция (оригинал), а её видоизменение (изображение). Это видоизменение производится при помощи умножения на некоторую экспоненциальную функцию и последующего интегрирования в определенных пределах.

Таким образом, применим преобразование Лапласа к дифференциальному уравнению (1):

L

8 T ( x , т )

8т

= L

8 ² T ( x , т )

8 x ²

Примем, что перепад температуры в беско нечно удаленной точке в грунтовом массиве от сутствует. Это допущение справедливо для габа ритов грунтового блока, в пределах которого про исходит теплообмен.

Приведем математическое описание вышеска занного.

Также выполним преобразование Лапласа к искомой функции Т (х, т):

L [ T ( x , т ) ] = J t ( x , т ) e ^- s ^т d т = T_L ( x , s ) .         (6)

Дифференциальное ности:

8 T ( x , т )     8 2 T ( x , т )

-----= a---;— 8т          8x ²

Краевые условия:

T ( x , 0 ) = T₀ = const;

T ( 0, т ) = Т с = const;

8 T ( +j , т ) = 0

8x        ’

уравнение теплопровод-

Далее выполним преобразование Лапласа левой части уравнения (5), которая представляет собой первую производную по времени от искомой функции T ( x , т ) .

Согласно основной теореме преобразования Лапласа преобразование от первой производной равно произведению изображения на оператор S минус значение функции в начальный момент времени, т.е.:

L

8 T ( x , т ) 8т

= ^sT L ( x , ^s )^{- T} ( x ) =

где T ( x , т ) – искомая функция распределения тем-

пературы внутри тела грунтового массива во времени ( т ) и глубине ( x );

т >  0 - время теплообмена выдерживаемого бетона конструкции и массива грунтового основания (сек.);

0 <  x <+j - координата, начало которой ( x = 0) соответствует поверхности грунтового массива, положительное направление – перпендикулярно плоскости хувглубь грунтового массива.

Физический смысл краевых условий:

• (2)    – в начальный момент времени температура во всех точках массива грунтового основания имеет постоянное значение;

• (3)    – поверхность полуограниченного тела в момент времени т = 0 принимает определенную и постоянную на протяжении всего процесса теплообмена положительную температуру;

• (4)    – отсутствует перепад температуры в бесконечно удаленной точке в грунтовом массиве.

Для решения дифференциального уравнения (1) при заданных граничных условиях (2)–(4) при-

⁸ 2 ^L [ T ( x , т ) ]    8 ² T l ( x , s )

= a----------= a Л 2    -

8x8

Преобразуем полученное уравнение (7) в более удобную форму с учётом краевого условия (2):

tL( x, s)-sTL (x, s)+T0 = 0.(8)

aa

Таким образом, дифференциальное уравнение (1) в частных производных для оригинала функции T ( x , т ) превращается в обыкновенное дифференциальное уравнение для изображения T_L ( x , s ) , поскольку T_L ( x , s ) не зависит от времени т .

Выполним преобразования по приведению подобных слагаемых и получим следующее дифференциальное уравнение:

T L ( x , s ) - ^s T L ( x , s ) - T 0 = 0.

a

a

Полученное неоднородное уравнение решается стандартными методами. Применим метод вариации произвольных постоянных, который изложен в учебниках по теории обыкновенных уравнений.

Общее решение данного дифференциального уравнения для изображения имеет следующую формулировку:

т„      . sx      -. sx

T L ( x , s ) - ^S = A 1 e a + B 1 ria ,           (10)

s

1⁵ T )

dQ, =-Х —    d т =

s

I^{д x} ; x = о

{ а s x

erferf

1 2 v o t .

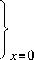
где А ₁ и В ₁ – постоянные, определяемые из граничных условий.

Применим преобразование Лапласа к краевым условиям (2)–(4):

Известно, что:

d dx

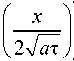
4 n a т

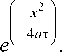
T

L [ T ( 0, t ) ] = L [ T c ] , T l ( 0, s ) = S ;             (11)

При x = 0 экспоненциальная функция равна

L

5 T ( +от , t ) 5 x

= 0, T L ( +« , t ) = 0.

единице. Получаем выражение для определения плотности теплового потока ( вт/м²):

Используя (12) применительно к (10), получаем:

q = d Q s = - Z f T oz T c ) =- Rc^Y ₍ t o _ t ₌ ) .   (21)

dτ        π a τ        πτ

0 = Tl («, t ) = £4 + ^B,e"   +

Из (13) следует, что постоянная A ₁ = 0 , так как в противном случае первый член правой части (13) не-

Количества тепла Q , отдаваемое выдерживаемой бетонной смесью за конечный промежуток времени выдерживания (τ _выдерж ) найдём путём интегрирования от 0 до τ _выдерж :

ограниченно возрастает и равенство не выполняется.

Для определения второй постоянной B 1 воспользуемся граничным условием (11) также применительно к (10):

Tc - T0 = B1 e ~ ^ = B1, ss откуда В1=-ri.                   (14)

s

Q =

^т выдерж /7

1 ^ * T o - T c ' d

t =

= 2^ ( T o - T _c ) S VТ выдер _Ж .             (22)

Тогда решение для изображения будет иметь

Запишем выражение (22) таким образом, чтобы выделить ту часть, которая представляет коэффициент теплопередачи:

Q = 2j^^CY— ( T o - T c ) S Т выдерж . (23) выдерж

вид:

^S - Tl ( x , s ) = ( S - T c ) ¹ e "^.            (15)

5                       5

Для нахождения оригинала воспользуемся таблицами изображений функций, из которой из-

вестно, что:

L 1

¹ e ^- k^

s

1 г I k = ^{1- erf} \

В нашей задаче k = -^=. Следовательно, по-

сле перевода изображения в оригинал получим:

T - T ( x , t ) = ( T o - T_c )

1 - erf

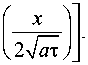
Окончательно решение выглядит следующим образом:

T ( x , t ) - T c T o - T_c

= erf

x

2 V o t

Таким образом, следующая часть выражения (23) представляет собой коэффициент теплопередачи массива грунтового основания:

λ c γ           λ c γ

^ гр.осн ².              1,¹³л          ,        ⁽²⁴⁾

выдерж          выдерж где λ,c,γ – соответственно коэффициент теплопроводности, коэффициент удельной теплоёмкость и плотность грунта. Выполняем проверку размерностей:

key = Дж Дж кг 1 =

V Твыдепж VC • М • К кг • К м³ С выдерж

Дж2      Вт2    Вт

=     4   2 2 =     4   2 = 2    .

v м • К • с Vm • К   м • К

Размерность выражения (24) полностью совпадает с размерностью коэффициента теплопередачи.

Получено решение дифференциального уравнения (1), однако оно не дает в чистом виде ответы

на поставленные вопросы.

Поэтому, используя полученное уравнение, определим потери тепла dQ_S за время d т через

единицу площади:

Выводы

С помощью теории теплопроводности, приёмов математической физики и теории дифференциальных уравнений удалось решить прикладную задачу и аналитически найти зависимость, определяющие величину тепловых потерь выдерживаемого бетона конструкции в грунтовый массив (23), и зависимость (24), определяющую величину ко-

Технология и организация строительного производства эффициента теплопередачи грунтового массива, которые можно использовать в дальнейших расчётах технологических параметров зимнего бетонирования.