Определение коэффициентов распределения напряжений в стальном листе при поперечном изгибе железобетонной балки
Автор: Бухман Николай Сергеевич, Жильцов Юрий Викторович
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Статья в выпуске: 6-2 т.15, 2013 года.
Бесплатный доступ
В статье представлены результаты определения коэффициентов распределения напряжений в поперечном армировании из стального листа в железобетонных балках на действие поперечной силы. Приведено сопоставление нормативной и предлагаемой методики расчета с опытными значениями.
Изгибаемый железобетонный элемент, поперечное армирование, наклонное сечение
Короткий адрес: https://sciup.org/148202539
IDR: 148202539 | УДК: 624.072.2.012.35
Текст научной статьи Определение коэффициентов распределения напряжений в стальном листе при поперечном изгибе железобетонной балки
Опытные исследования на железобетонных образцах [1] с применением тензометрического измерения деформаций на стальном листе и бетоне, показывают, что поперечное армирование из стального листа в зоне поперечного изгиба находится в плосконапряженном состоянии. В стальном листе одновременно действуют нормальные и касательные напряжения, в связи с чем площадка главных растягивающих напряжений находится под углом к продольной оси балки. Расчет наклонного сечения с жестким поперечным армировани- ем на действие поперечной силы по нормативному документу [2] не учитывает плосконапряженное состояние стального листа и угол наклона главной площадки растягивающих напряжений, что при расчете приводит к значительному расхождению с фактической несущей способностью. Автором [3] предлагается условие прочности железобетонных балок по наклонному сечению, позволяющее учесть плосконапряженное состояние поперечного армирования из стального листа.
Q b + Q eep + Q s + Q t = R bt • b • h 0 •
к + k2

+ кж 1 Rcm t cmC 0 +
где Q b , Q s - поперечное усилие воспринимаемое бетоном и поперечное усилие, воспринимаемое продольной арматурой, соответственно [4]; Q верт и Q т - вертикальное и касательное усилие, воспринимаемые стальным листом, предложенное автором [3].
Плосконапряженное состояние стального листа учитывается введением коэффициентов к ж1, к ж2 в Q верт и Q т. Коэффициенты учитывают взаимосвязь условия прочности стали при действие двухосного напряженного состояния и имеют зависимость между собой в виде (2)
k ж2
1 - к 2
ж1
V з
Определение коэффициентов к ж1, к ж 2 сводится к решению равенства (3) в котором одновременно увязан угол наклонна главной площадки напряжений, с проекцией критической наклонной трещины и уравнением прочности плосконапряженного
R s A c c 0 h o Y v
+
состояния стали.
h - х
h о Л 3
1 — к ж1
1 + к ж1
k ж 2 R ст Jt ст
S 0,5 сечения
2 k 2 • R bt • b
0,4
k R t + Rs • As k ж1 • R cm " tcm + У---- *
I h о • Y v J
Решение уравнения (3) выполняется аналитически. Для отыскания коэффициентов рассмотрим диапазон изменения входящих в формулу прочностных характеристик материалов, геометрических характеристик и коэффициентов:
80 < ho < 700.15 < х < O,5ho.1OO < b < 700. ; ;;
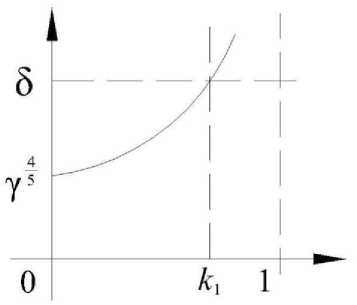
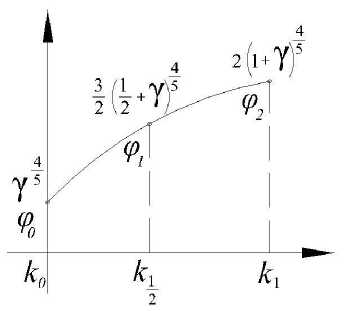
0,7 1,5 < tcm< 30 . 200<Rm<415. 215<R<500. ст ст ;;; 400 < 4< 6000 5 < /* < 22 s ; v. С целью упрощения решения произведем замену: ^ х ; I h 0 J ; ^^ 3 к 2 • Rbt • b 2 R • t ст ст ; Y = Rs • As ho • Y* • Rem • tom У = (2 + У1 + 51) — — (20/1151) 5Yi После преобразования выражение (3) примет вид: 2|1 + 5 V 5Y1. 2|1 + А_ V 5Y1. a2• 1 + k J 1 - kJ в5 (k + Y )5 Тогда в первом приближении значение k с учетом того, что k≥0 будет: Тогда k в уравнение (4) будет существовать при выполнении условий: Y4 < — Y2< S 5 2< /?2 Y " a10 • Y " a5 • a Y ^ P ; ; . k = 1 — (2 + Y1 + 51) 2|1 + P1-V 5Y1. , I(Y1 + 51) • (Y1 + 51 + 4)— (20yl±5i) 5Y1 На рис. 1 представлен график зависимости γ от k. Рис. 1. График зависимости γ от k Умножим выражение (4) на (k + γ) и получим: (k + YX1 + k= ^ (k + y )L 1 — k a Принимая для уравнения (5) вторую замену 4 5 = a2 • в5; y =1 - k; k=1 - y (при этом y<1) полу чим: (1+ Y — у X2 — у) = 5(1+Y — у )5 у (6) В первом приближении из (6) получим: Произведем уточнение kж1 методом аппроксимации. Для уточнения в уравнении (4) произведем замену δ=β4/5/α2. Предположим, что степень есть р=4/5, тогда степень можно записать как р=4/5=1 – 1/5=1 – v, в этом случае k является функцией от v, то есть k=k(v) где v=1/5, тогда уравнение (4) примет вид: 1 + k _ 5 1 — k (k + y)1—v Решим функцию при v=0, то есть k0=k(0) – ? Подставим v=0 в (11), получим квадратное уравнение: k0 +(1 + Y + 5)ko +(y — 5) = 0 (12) Решением уравнения (12) будет: 7 (1 + Y + 5 )2+ 4-(5 — Y) — (1 + Y + 5) Если предположить, что в формуле (12) k=0, тогда 5>у4/5. Если k = 1, тогда k = 1 - Ak, Ak<<1, уравнение (11) примет вид: 2 —Ak 4 —— (y +1 — Ak )5= 5 Ak В нулевом приближении уравнения (14) будем иметь следующее 5(1 + Y — У )5= 5(1 + Y )5 1—1• -у- 5 1 + y Произведем третью замену подставив в (7) 1 Y1 = 1 + Y, 5 = 5 • y5 и перенеся все в левую часть, получим квадратное уравнение: 2(1 + /)4 = 5Ak Ak(0) = 254 (1 + /)4 ; Выразим k(0) из (14): k (0) = 1 — 2 (1+1)1 5 (16) у I1+51) V 5/iу — (2 +Y1 + 51)У+2Y1 = 0 Произведем уточнение: Ak = 5 ■' (2 — Ak)(/ +1 — Ak )5 = 5"‘ (2 — Ak )(1 + y )5 Решением квадратного уравнения будет: Ak 5 l+Y _ = 5 2(1 + /)5 Ii—Ak J|i—^2 JI5 V 2 X 1 + Y J = 23 (1 + y)5 1+ A к( — 1 I 2 = 23 (1 + у)5 ( 11 ^ 4 1— I + I-23 (1+ у)5 V 2 1 + y ) Тогда, выразив 5, получим условие существования уравнения: 1+-J -(1 + y)5 << 3 Рис. 2. График зависимости функции ф(к) Условие (18) выполняется, если: ( 4) 3 >> 1, y5 . 3 >> (1 + Y)5 • 3 >> (1 + y)5 Для упрощения решения (22) запишем: Условие (19) выполняется при к = 1. Если к ~ 1, тогда (11) есть функция: а = „ 4 / 1 ^ 5 4 2y5— 6I Y + I + 4(Y +1)5 f = FI "7 +k)5= 3 1 - к Рассмотрим функцию: ф к) = (1 + к )-(y + к )4 Предполагая схожесть (21) с (a+bx+cx2) при 0 Ф(к) ~ Фо с = Y5 +Фх (к — к0 Xк — к2 )+ ф (к1 — к0 Xк1 — к2 ) 2 (к — к1Xк — к2 ) (к0 — к1Xк0 — к2 ) (к — коXк — к1) (к2 — к0 Xк 2 — к1 ) = y5 3 (1 )5 (к — 0)(к —1) +2V 2 + Y J (1 J( 1 У + 2(1 + Y )4----И2 (1 — Т —2 = к22y5 — 15 4 6I Y + -1 + 4(Y+1)5 + . 4 ( 1 4 5 + к — 3y5+ б| y + - I V 2 4 — z х 4 - 2(Y+1)5 +Y = ак2+ bk + с Найдем решение уравнения (22). Перенеся все в левую часть, получим квадратное уравнение: ak2+(b + 5)к + (c - 5)=0 (23) С учетом того, что к>0 окончательным решением квадратного уравнение будет: к_ л[ (b + 3 )2— 4 а (с — 3) —(b + 3) 2 а (24) Тогда коэффициент кж1 полученный из уравнения (3), и коэффициент кж2 с учетом (2) можно записать: k (b + 3)2— 4 а (с — 3) — (b + 3) 2а 1 — у (b + 3 )2— 4 а (с — 3) —(b + 3) V 2а где a, b, c, 5, а, в, Y замена, принятая для упрощения отыскания коэффициентов: а = b = \ . 4 / 1) 5 4 2y5— 6I y + _| + 4(y +1)5 1 4 / 1)5 — 3y5+ 6I y + I V 2 4 — 2(Y+1)5 с = Y 5 в 5 а = -1 1 — х ; в = 3 k2 • Rbt - b 2 Rcm " tcm • ; ; V hо ) . ; Rs • A Y =---г—5-- h0 • Yv • Rcm • tcm Найденные выражения для коэффициентов kж1 и kж2, позволяют учесть напряженно-деформированное состояние поперечного армирования из стального листа. Подстановка фактических прочностных и геометрических характеристик опытных образцов из [1, 5] в условие прочности (3) с учетом коэффициентов распределения напряжений kж1 и kж2 для определения несущей способности по наклонному сечению показывает лучшую сходимость расчетных и опытных значений по сравнению с нормативными методиками [2, 6]. Результаты сопоставление приведены в табл. 1. Таблица 1. Сопоставление расчетных и опытных значений несущей способности Марка образца сФакт, мм Qроп, кН Qрт, кН [6] Qроп/ Qрт [6] Qрт, кН [2] Qроп/ Qрт [2] Qрт, кН [1] с kж1 и kж1 Qроп/Qрт [1] с kж1 и kж1 Б1-Вс 294 290 202,73 1,43 139,62 2,08 265,09 1,09 Б2-Вс 294 289 216,69 1,33 147,74 1,96 280,27 1,05 Б3-Вс 192 380,5 239,13 1,59 147,83 2,58 353,98 1,075 Выводы: сопоставление расчетных и опытных значений прочности показывает, что существующая нормативная методика [2] значительно недооценивает прочность наклонного сечения железобетонных конструкций с жестким армированием. Сопоставление по методике [6] носит оценочный характер, но при этом также значительно недооценивает несущую способность. Предлагаемая методика [1] учитывающая плосконапряженное состояние поперечного армирования из стального листа, наиболее удовлетворительно оценивает несущую способность наклонного сечения и может быть применима для выполнения расчетов наклонного сечения с поперечным армированием из стального листа.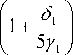
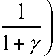
Список литературы Определение коэффициентов распределения напряжений в стальном листе при поперечном изгибе железобетонной балки
- Жильцов, Ю.В. Работа наклонных сечений изгибаемых железобетонных элементов с жестким поперечным армированием//Бетон и железобетон. 2012. №6. С. 11-16.
- Руководство по проектированию железобетонных конструкций с жёсткой арматурой. -М.: Стройиздат, 1978. С. 55.
- Жильцов, Ю.В. Новый подход в расчете железобетонных балок армированных жесткими вставками на действие поперечной силы//Строительный вестник Российской инженерной академии: труды секции «Строительство» РИА. Выпуск 11. -М., 2010. С. 157-159.
- Карпенко, С.Н. Построение критериев прочности железобетонных конструкций по наклонным трещинам разрушения//ACADEMIA архитектура и строительство. 2006. №2. С. 54-59.
- Филатов, В.Б. Особенности работы и эффективное использование жесткой поперечной арматуры железобетонных балок/В.Б. Филатов, Ю.В. Жильцов//Известия Самарского научного центра Российской академии наук. 2012. Том 14 №4(5). С. 1324-1328.
- СНиП 2.03.01 -84*. Бетонные и железобетонные конструкции. Нормы проектирования. -М.: Стройиздат 1991. с. 77.


