Определение коэффициентов трансформации воздушного потока при воздействии на одиночное здание c использованием технологий компьютерного моделирования

Процессы урбанизации городов ставят новые задачи перед градостроителями, в круг которых входит создание безопасной и комфортной среды. Одно из наиболее оптимальных направлений для оздоровления воздушного бассейна – это всесторонний учет аэрационного режима местности, при котором исследуются закономерности движения воздуха с учетом естественного и техногенного рельефа. Аэрация населенных мест – процесс естественного регулируемого проветривания территории городов и других населенных мест [1].

В процессе аэрации происходит трансформация воздушного потока в результате взаимодействия его с природным и антропогенным ландшафтом. Трансформация заключается в изменении скорости и направления ветра. Для того чтобы прогнозировать аэрационный режим на территории населенного места, необходимо изучить этот процесс, построить его теоретическую модель. Далее – определить каналы получения необходимой для расчета информации о качественной и количественной характеристике этого процесса и разработать методику расчета. Подобные методики уже разрабатывались ранее и подробно освещены в трудах Ф.Л. Серебровского, Э.И. Реттера и др. [1, 2], где выполнялись теоретические и экспериментальные исследования процессов аэрации городскихи нарушенных территорий [3, 4].

Проанализировав ряд существующих исследований, а также оценив перспективы развития данной области, можно выделить следующие обобщенные методы решения задач обтекания воздушным потоком профиля техногенного рельефа:

• •    теоретические методы решения (например, метод источников и стоков [1]);

• •    экспериментальные методы (практические);

• •    методы численного моделирования или вычислительной гидродинамики.

В настоящее время существует большое множество методик и прикладных программных средств, предназначенных для выполнения компьютерного моделирования ветровых воздействий на здания и сооружения методами вычислительной гидродинамики (CFD) [5].

Получение и анализ исходных данных физического эксперимента

В данной работе рассмотрен пример проведения математического моделирования на основе полунатурного эксперимента с последующей попыткой верификации оригинальных результатов, полученных в ходе эксперимента на масштабных моделях в аэродинамической трубе.

Цель верификации и сравнения результатов вытекает из особенности построения расчетной модели, так как в рассматриваемом случае математическое моделирование производится для «полного» случая с «полным» геометрическим и кинематическим подобием модели. В качестве опорных характеристик, на основе которых будут сравниваться результаты моделирования и эксперимента, предложено использовать коэффициенты трансформации воздушного потока, которые используются в исследованиях процессов аэрации жилой застройки.

Известно, что воздушный поток, обтекающий различные формы техногенного рельефа, трансформируется как по величине скорости, так и по направлению движения. Существуют две основные характеристики, определяющие изменение скорости и направления ветра в каждой точке рассматриваемого пространства, – это коэффициент трансформации τ i и угол трансформации воздушного потока Δ α i .

Таким образом, зная скорость и азимут ветра в заданном географическом пункте (на основе многолетней статистики и розы ветров), а также значения вышерассмотренных коэффициентов, можно определить характеристики аэрационного режима на рассматриваемой территории.

Проанализируем исходные данные оригинального эксперимента, особенности организации экспериментальной установки и выходные результаты. Основная сложность, возникающая при физическом моделировании аэродинамических процессов, заключается в невозможности отображения реальной картины в условиях малогабаритной аэродинамической трубы.

Очевидно, что при масштабировании исследуемого случая до подходящих размеров необходимо соблюсти геометрическое, кинематическое и динамическое подобия сред [6].

В качестве меры геометрического подобия можно использовать коэффициенты L_m и L_n , определяющие соотношение линейных размеров реального объекта и его модели соответственно. В исходном эксперименте масштаб был выбран 1:1000.

Для достижения кинематического подобия воздушной среды необходимо воссоздать условие переменности по вертикали профиля скорости потока. Данное условие в исходном эксперименте обеспечивалось путем установки на срезе трубы специальной решетки с переменным шагом отверстий соответственно приращению координаты высоты относительно модели [7, 8].

Динамическое подобие моделируемого воздушного потока натурному можно обеспечить путем достижения подобия структуры турбулентности, характеризуемой скоростью диссипации турбулентной энергии, а также равенством турбулентных чисел Рейнольдса. Число Рейнольдса имеет большое значение в экспериментальной аэродинамике, оно определяет подобие по силам вязкости. Соблюдение постоянства числа Рейнольдса в натурных условиях и в эксперименте обеспечивает корректный учет эффекта вязкости [9, 10].

Исходный аэродинамический эксперимент основан на теории подобия, а исследования в этой области показали, что скорость воздушного потока в аэродинамической трубе может варьироваться в пределах U N (L m /L n )^1/3 ≤ U m ≤ U N , где U m и U N – средние скорости воздушного потока при моделировании и в натурных условиях [1].

Имеем следующие исходные данные для эксперимента:

• •    линейные размеры модели: L_m/L_n = 0,001;

• •    скорость потока в аэродинамической трубе U m = 0,1 *U N .

В исходном эксперименте Ф.Л. Серебровско-го осуществлялось моделирование характерного случая обтекания воздушным потоком отдельно стоящего здания линейного типа, именно на данном упрощенном примере можно пронаблюдать наиболее характерные области и коэффициенты трансформации воздушного потока для последующей оцифровки эксперимента. По результатам данных испытаний было построено поле относительных скоростей в сечении по оси симметрии (рис. 1). Также были нанесены линии тока, полученные расчетным методом источников и стоков (рис. 2) [1, 11, 12].

На рис. 3 изображено векторное поле скоростей в приземном слое толщиной 2 м (в натуре) с изолиниями и векторами скоростей. В данном случае высота в 2 метра обусловлена высотой роста человека, именно в этой зоне формируется наибольшее влияние на климатический комфорт для человека [1].

Полученные экспериментальные данные позволяют создать представление о движении воздуха в окрестностях одиночного здания, а также о характере образующихся вихрей на передних кромках здания.

Данные изображения, полученные аналитическими методами, а также в ходе полунатурных экспериментов в аэродинамической трубе, далее были использованы как референсные образы для дальнейшего сравнения с результатами численного моделирования. Основной упор делался на графическое сравнение результатов с интерпретацией коэффициентов трансформации в ярко выраженных характерных областях [13].

Ход эксперимента

Расчет проводился по следующему алгоритму:

• 1.    Подготовка расчетной модели:

• •    создание объемной геометрической модели, описывающей расчетную область. Этот пункт был выполнен в программном комплексе SolidWorks;

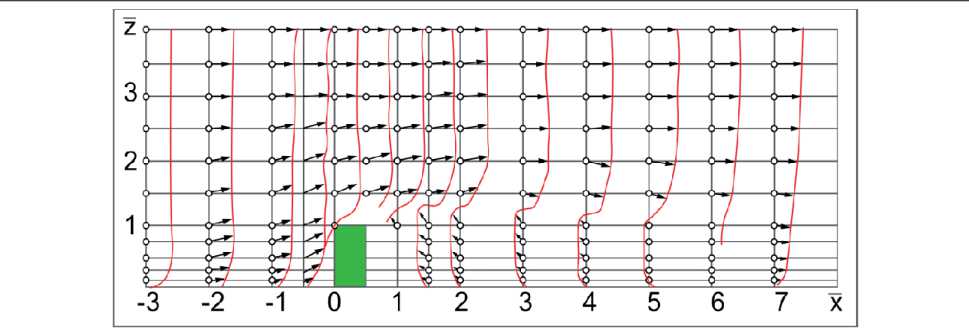
Рис. 1. Поле скоростей по оси симметрии здания

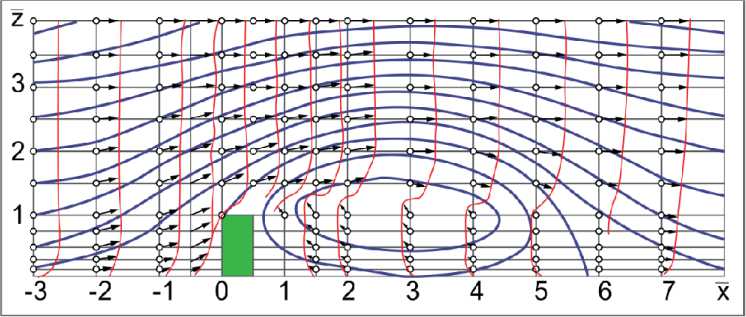
Рис. 2. Поле скоростей по оси симметрии здания c линиями тока, полученными расчетным методом

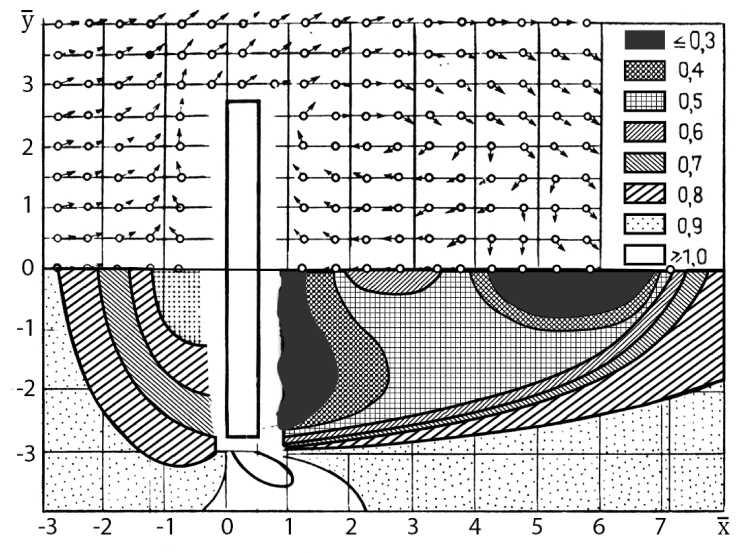
Рис. 3. Поле скоростей и значения коэффициентов трансформации воздушного потока в приземном слое на высоте 2 м (в натуре)

Рис. 4. Модель расчетной области с построенной сеткой КЭ

• •    генерация с е точной м одел и на ос нов е с о зда н ной ге ом етри и. Э тот пу н кт бы л в ыполнен в па кете програ м м ного ком пл екс а A NSY S MESHING;

• •    з а д ан ие гран ич н ы х и на ч а ль ны х у сл о вий, в ыбор физической модели расчета – пр епро це сс и н г.

• 2 .    Р е ше ние з а да чи в ра с че тн ом м одул е .

• 3.    Прос мотр и оц ен ка ре зульта тов – постобработка.

Дл я а нализ а бы л а с оз да на вирт уал ь на я м оде л ь зд ан и я с ра з м е ра м и, отв е ча ющим и у с л овиям исх одного по лу на т у рного экс п е рим е нта [1]:

S×H =6,                                (1)

где S – ши рина з дани я (в а э род ина м иче ском с м ы сле); H – высота здания.

Дл и на з дани я в ра с че тах н е уч итыв а етс я и в э кс пе рим е н те бе ре тс я ра вн ой в ыс оте – 10 м, ширина здания – 60 м.

Ра з м е ры ра с че тной обл а с т и в ыбирал ис ь та к им о б ра зом , чтобы е е гра ницы не ока з ыв али вл и ян ия на ре з у л ьтаты ра с че тов , для этого в ыбира е тс я х арактерный размер объекта H _max – размер объекта в р а с с м а трив а е м ой п л ос кос т и; в данном случа е з а х ара кте рны й ра з м е р обл а с т и прин им а е тся ш ири на здания – 60 м . Д ля из олиров а нны х зда н ий ре к оме нд уе м ые ра з м е ры ра с четной об л а с т и с л е д ующие [7, 8]:

А ≥ 5 Н max – расстоя ние о т центра объ е кта до края расчетной области;

В ≥ 5 Н max – р а с с тояние о т центра объ е к та до границы Inlet (вход);

С ≥ 15 Н max – р а с с тояние от це н тра объ е кта до границы Outlet (выход);

D ≥ 6 Н _max – о б ща я в ы с ота ра с че тной об л а с т и;

H _max – р а з м е р объ е кта в рассматриваемой плоскости.

Таким образом, расчетная область построена с размерами: ширина – 600 м, длина – 600 м, высота – 100 м.

При проведении эксперимента методами конечно-элементного моделирования решающее значение в достижении точных результатов расчета имеет качество построения сетки конечных элементов (КЭ).

Плотность сетки при подготовке эксперимента регулировалась указанием максимальной величины для грани конечного элемента (параметр Max Face Size). Для параметра была выбрана величина в 2 м. Максимальный размер грани в выбранной области вокруг здания был взят 0,5 м. В результате была получена сетка конечных элементов, состоящая из 5470034 элементов (рис. 4).

Опыт исследований в аэродинамической трубе показывает, что при выполнении эксперимента необходимо соблюдение геометрического, кинематического и динамического подобий.

Геометрически эксперимент полностью воспроизводит реальные размеры здания. Кинематическое и динамическое подобия набегающего воздушного потока обеспечиваются программным комплексом ANSYS и анализом FluentFlow.

Условия изменения профиля скорости с высотой в расчетном модуле ANSYS Fluent задаются с помощью подключения к граничным условиям таблицы данных со значениями скоростей в формате csv.

Средняя скорость потока принята 15 м/с, поток направлен под прямым углом к зданию.

Результаты моделирования и сравнение с первоначальными данными

После расчета была получена картина распределения потока воздуха, схематически разбитого с по- velocity

ANSYS

Я18.2

Contour 2

г-г 3.052e+001

1 2.891e+001

- 2.731e+001

■ 2.570e+001

- 2.409e+001

- 2.249e*001

- 2.088e+001

• -    1.9286+001

• ■    1.7676*001

• - 1606e+001

• -    1,446e

• ■    1.285e+001

• -    1.1246+001

• -    9.638e+000

• ■    8.0316+000

• -    6.4256+000

• -    4 8196+000 ■ - 3.2136+000 ■ - 1 .6066+000 ■ 0 0006+000

  

  Рис. 5. Схема распределения скорости в симуляции в плоскости XY на высоте 2 м над землей

  
  
  

  Рис. 6. Схема распределения скорости в симуляции в плоскости ZX на высоте 2 м над землей

  
  

м ощь ю ф у н к ц и и пост про цесс ора c o nt o u r н а 20 з н ачений скорости (рис. 5, 6).

Дл я с ра вне н ия с ре зу л ьтатам и а налит иче с к их расчетов и п олу нат ур ных экс пе рим е н тов бы л и в зяты проб ы з на чен ий с к орос ти в х а ра кте рны х точках расчетной области.

П о ре з у л ьта та м ана лиз а бы л и получены с л е дую щи е з н ачен ия, с гр у пп и р ов ан ные в таб л и ц е.

Для сравнения общей качественной картины результатов численного моделирования с результатами аналитических и полунатурных методов поле скоростей, полученное в результате компьютерного моделирования, было графически наложе- но на схемы распределения коэффициентов трансформации (рис. 7, 8).

Выводы

Проведено численное моделирование по исходным данным в реальных масштабах, полученные данные были совмещены на одном графике для сравнения.

Очевидно, что полученные данные подтверждают сходимость и воспроизводимость изначальных экспериментальных данных, а факт высокой схожести выходных коэффициентов трансформации и общей схожести качественной картины

Сравнение результатов анализа поля скоростей в частных точках при компьютерном моделировании с данными, полученными в аэродинамической трубе

Коэффициент трансформации воздушного потока в области	Значения скорости, м/с	Среднее значение скорости, м/с	Отклонение от расчетного значения, %
менее 0,3	6,3	7,6	21
	7,6
	8,8
0,4	6,7	8,7	18
	8,5
	10,8
0,5	5,8	7,9	3
	7,6
	10,4
0,6	8,9	11,1	14
	9,5
	14,8
0,7	10,8	12,5	13
	12,3
	14,1
0,8	11,5	13,3	9
	12,3
	16,1
0,9	14,2	16,2	18
	16,3
	18,1

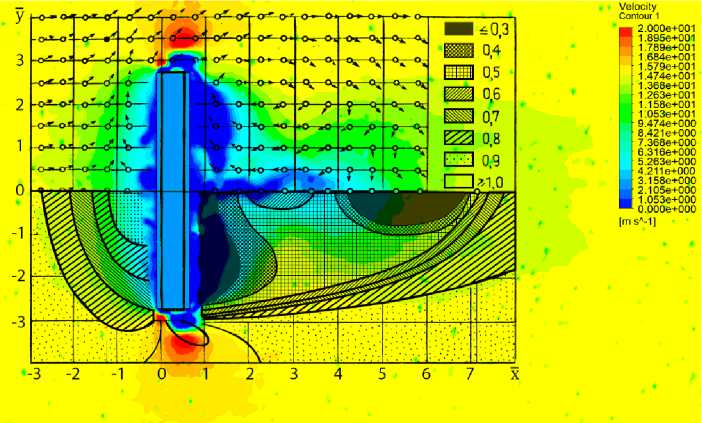
Рис. 7. Сравнение поля скоростей, полученного в результате численного моделирования, с полем коэффициентов трансформации, полученным опытным путем в горизонтальном сечении на высоте 2 м (в натуре)

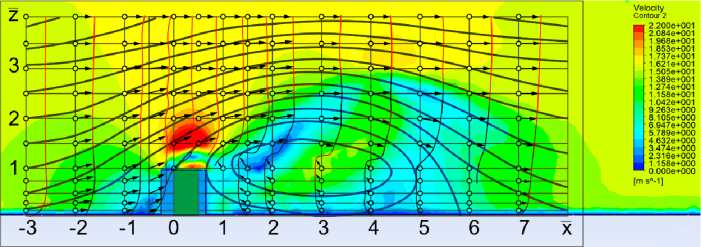
Рис. 8. Сравнение поля скоростей, полученного в результате численного моделирования, с полем коэффициентов трансформации, полученным аналитическим и опытным путем с высокой долей вероятности может свидетельствовать о достоверности результатов исходного эксперимента.

Численное моделирование данного частного случая в реальном масштабе с разными настройками плотности расчетной сетки, а также качества моделирования позволили дополнительно уточнить результат путем получения информационной избыточности, при этом итоговые данные все равно сохранили качественную картинку и общий характер распределения.

Полученные в ходе сравнения данные подтверждают правильность настройки исходной модели и расчетов, следовательно, данная методика может быть использована как отправная точка для дальнейших исследований с применением технологий численного моделирования других более сложных случаев обтекания и ветрового воздействия на техногенный рельеф.