Определение контактного давления при прокатке двутавровых профилей в универсальном балочном калибре

Наиболее эффективным способом производства двутавровых профилей различного типа (балочных, широкополочных, колонных и др.) является прокатка на современных универсальных рельсобалочных станах, снабженных универсальными балочными клетями (рис. 1) [1, 2]. При проектировании и освоении технологических режимов прокатки таких изделий необходимо рассчитывать давление и усилия прокатки на горизонтальные и вертикальные валки универсального балочного калибра. Используемые для этого известные теоретические методы расчета давлений и сил базируются в основном на совместном решении упрощенных дифференциальных уравнений равновесия и уравнения пластичности [2–4]. Применяемые в указанных методах гипотезы, допущения и эвристические приемы снижают точность определения

контактных давлений и усилий деформации, что требует корректировки и доработки рассчитанных технологических режимов при их освоении в производственных условиях.

Наиболее точные результаты могут быть получены на основе анализа полной системы уравнений теории пластичности [5]. Ниже представлено решение задачи по определению контактных давлений и усилий прокатки в универсальном калибре на основе использования физических уравнений связи напряженного и деформированного состояния металла в очаге деформации.

Для определения напряженного и деформированного состояния металла при прокатке двутаврового профиля в универсальном четырехвалковом калибре (рис. 2) была поставлена и решена задача с применением вариационного принципа

УК1 ВК УК2                 УКВ

Рис. 1. Схема расположения рабочих клетей современного типового рельсобалочного стана: 1 и 2 – обжимная и черновая реверсивные клети дуо; 3 – чистовая непрерывно-реверсивная группа: УК1, УК2 универсальные реверсивные клети; УК3 – чистовая нереверсивная клеть; ВК – двухвалковая сдвигаемая вспомогательная клеть

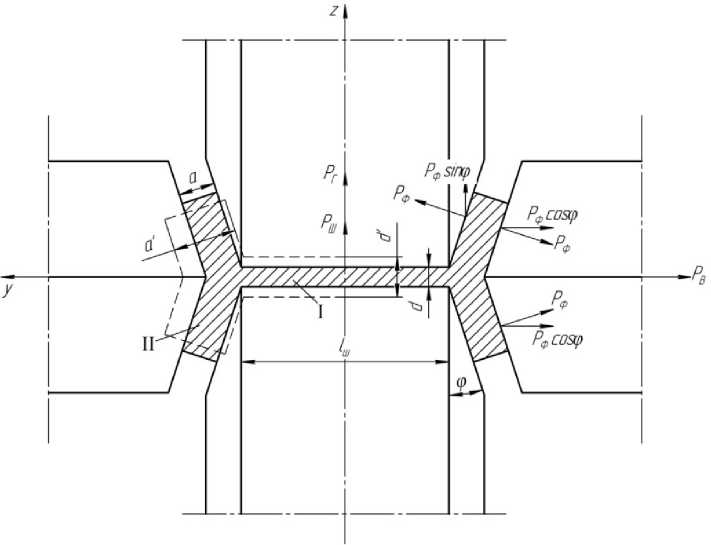
Рис. 2. Схема прокатки двутаврового профиля в универсальном калибре и обозначение сил, действующих на горизонтальные и вертикальные валки (пунктирной линией показана ½ часть задаваемого профиля)

минимума полной мощности [6]. При этом деформацию шейки I и фланцев IIрассматривали как прокатку прямоугольных полос на гладкой бочке валков, причем полагали, что обжатие фланцев происходит только со стороны вертикального валка. По результатам решения такой задачи с использованием известных положений механики [5] определили компоненты тензора скорости деформации р у и интенсивность деформации сдвига Н . С учетом этого, физические уравнения связи напряженного и деформированного состояния для изотропной среды записывают в виде [5]:

о j —о5 _у = ( Р j —Р5 j /3)2 T / Н ,            (1)

где Т - интенсивность касательных напряжений.

В системе уравнений (1) имеем 6 неизвестных и всего 5 независимых уравнений, поскольку среднее напряжение о = о ii / 3 . Поэтому, система уравнений (1) является незамкнутой. Чтобы замкнуть эту систему, использовали выражение для интенсивности касательных напряжений Т . Поскольку задачу решали для жесткопластической среды, то Т = т ₅ , и следовательно, с учетом зависимости Т от компонентов тензора напряжений [5] сопротивление деформации металла на сдвиг

ts Т       Вв.                             (2)

S 6

где

B = (°xt — о )2 + (о —о )2 + (о —о)2 + xx yy         yy zz         zz xx

+ 6(о2 + о2 + о^) .

xy yz zx

Путем несложных преобразований в системе уравнений (1) получим выражения для 5 неизвестных компонентов тензора напряжений:

^о хх

о yy

о

xy

^о yz

о zx

=т5 (3р хх+р yy — Н

р _zz );

^ ₍э р хх + 5 р yy + р zz );

= 2т5 р •

Н ^{р xy ;}

= 2Т5 р •

н ^р yz ^;

= 2Т5 р

Н z" . .

Для нахождения последнего компонента тен-

зора о zz использовали уравнение (2), в результате

чего получили

о zz

^{( о} yy ^{+ о} хх ) ⁺ У ^{( о} yy ^{+ о} хх ^{) 2 + 4} A

где A = 3 т ₅

22    222

— о — о + о о  — 3(о  + о + о ) .

xx yy xx yy xy yz zx

Полученные выражения (3) и (4) позволили определить все 9 компонентов тензора напряжений (с учетом парности касательных напряжений). Сопротивление металла сдвиговой деформации т ₅ определяли методом термомеханических коэффициентов [7].

Для определения напряжений, действующих на произвольной площадке поверхности контакта (положение которой определяется нормалью), раз-

Обработка металлов давлением ложили вектор полного напряжения р на три со- ставляющие [5]:

P_x = g n_x + g n_v + сП; ; x xx x xy y xz z

P y = ^ xy n x +C yy n y +G yz n z ; P z = ^ xz n x +C yz n y +C zz n z ,

где nx, ny, nz – направляющие косинусы, определяющие положение площадки относительно осей координат.

В нашем случае направляющие косинусы равны

X л      1 h - h nx = —, nv = 0, nz =-1 +------.           (6)

x R y z          R

Направляющие косинусы (6) единичной нор мали удовлетворяют условию nX + ny + nz = 1 в каждой точке поверхности контакта.

Подставляя выражения (6) в систему уравнений (5), нашли каждую составляющую и опреде- лили полное контактное напряжение в точке

P = Pp + ⁺ P y ⁺ P z .

Среднее контактное давление определили в результате интегрирования давления в точке по поверхности контакта S_k и деления на площадь контактной поверхности

JJ PdS k

^{P ср}    J S '                                  ⁽⁸⁾

S k

Средние нормальные напряжения рассчитывали с учетом напряжений контактного трения ттр отдельно в зоне отставания Sот и опережения Sоп pnср

\ ^P ср   ^Т тр ,

где т _тр = ^т S (v - показатель трения [2]).

Зная нормальные напряжения в каждой зоне очага деформации, находили усилия, действующие на шейку Р _ш и фланцы Р ф (см. рис. 2) по общей формуле

P = JJ P n ср ■ V 1 + ( h ( X )')² dS от + от

+ JJ P n ср^/ 1 + ( h ( x )')² dS оп .                   (10)

S оп

При определении полного усилия на горизонтальный валок учитывали вертикальную составляющую силы, действующей со стороны фланца Р ф sin ф (см. рис. 2):

Р _г = Р ш + 2 Р ф sin ф .                      (11)

Горизонтальное усилие, действующее на вертикальный валок, определили с учетом угла наклона фланца ф (0 < ф < п /4)

Р в = 2 Р ф COS Ф .                           (12)

При этом полагали, что силы Рф , действую- щие на конических поверхностях вертикального и горизонтального валков равны.

Разработанный метод определения контактных давлений и сил прокатки был реализован в виде программ расчетов с использованием вычислительного пакета Mathcad на персональном компьютере. С целью экспериментальной проверки этого метода расчеты проводили для условий прокатки двутавровых профилей № 35Б1, 40К2 и 45Б2 из стали 15ХСНД на универсальном балочном стане ОАО «НТМК». Полученные расчетные данные сравнивали с результатами экспериментальных исследований [8, 9], оценивая сходимость расчетных и опытных данных по формуле A P = ( ^Р рас - ^Р оп)/ ^Р оп , %.

Результаты такого анализа представлены в таблице. Как видно, результаты расчетов имеют

Расчетные и опытные данные при прокатке двутавровых профилей в универсальной клети ГУК-2 УБС ОАО «НТМК»

Номер прохода Толщина, мм Коэф. вытяжки λ Опытные значения усилий, МН Расчетные значения усилий, МН Отклонение по отношению к опытным значениям, % Стенки Фланцев d' d a' a Pг Pв Pг Pв ΔPг ΔPв 35Б1 1 9,9 8,3 15,6 12,8 1,193 2,98 1,38 2,18 1,26 –26,9 –8,7 2 8,3 7,1 12,8 10,8 1,169 2,62 1,5 1,95 1,12 –25,3 –25,5 3 7,1 6,2 10,8 9,3 1,145 2,35 1,46 1,74 0,99 –25,9 –32,5 40К2 1 18,7 16,6 29,8 25,8 1,126 2,34 1,7 2,3 2,35 –1,7 38,6 2 16,6 14,9 25,8 22,7 1,114 2,14 2,2 2,12 2,14 –1,2 –2,6 3 14,9 13,6 22,7 20,3 1,096 1,86 1,95 1,8 1,84 –1,2 –5,6 45Б2 1 12,9 11,4 20 17,4 1,132 2,71 1,43 2,95 1,40 8,9 –1,8 2 11,4 10,2 17,4 15,4 1,118 2,47 1,74 2,89 1,37 17 –21,3 3 10,2 9,2 15,4 13,9 1,109 2,25 1,65 2,75 1,29 22,2 –21,8 удовлетворительную сходимость с экспериментальными данными. Среднестатистическая погрешность расчетов составляет 6,4 %.

Выводы

• 1.    Разработан новый теоретический метод расчета контактных давлений и усилий прокатки в универсальном балочном калибре, основанный на использовании физических уравнений связи напряженного и деформированного состояния металла в очаге деформации.

• 2.    Достоверность разработанного метода подтверждена результатами экспериментальной проверки.

• 3.    Новый метод рекомендуется применять при расчете калибровок валков и технологических режимов прокатки двутавровых профилей на рельсобалочных и сортовых станах, снабженных универсальными клетями.