Определение координат проекции точки пространства на матрицы камер в стереопаре

В настоящее время для определения координат точек пространства широко используется техническое (компьютерное) зрение, основанное на применении стереоскопической пары видиокамер, оптические центры которых разнесены в пространстве, а их оптические оси параллельны друг другу. Восстановление координат точки пространства происходит на основе пары ее снимков, полученных одновременно с двух камер.

При установке оборудования добиться идеальной параллельности оптических осей практически невозможно. Поэтому для корректировки ошибки, возникающей при нарушении параллельности оптических осей, предлагается разрешающая система двух нелинейных уравнений.

1. Постановка задачи

Пусть оптические оси камер отклонены навстречу друг другу на одинаковый угол 0,1 ° , что отвечает максимально допустимому значению.

Далее используются следующие значения для параметров стереопары: фокусное расстояние f= 10 мм ; стереобаза b= 5 м ; угол пересечения оптических осей ф= 0.2 ° ; размер одного пикселя 0.0055 мм .

В качестве входного параметра задаются пространственные координаты рассматриваемой точки. Требуется разработать алгоритм и программу расчета координат проекций этой точки на матрицы камер стереопары.

Рассмотрим 2D случай в плоскости XOY (Рис. 1). Здесь наблюдаемая точка движется прямолинейно вдоль верхней стороны трапеции, в нижних вершинах трапеции располагаются видиокамеры, боковые стороны трепеции отвечают оптическим осям камер; углы, выходящие из нижних вершин трапеции, отвечают углам обзора камер.

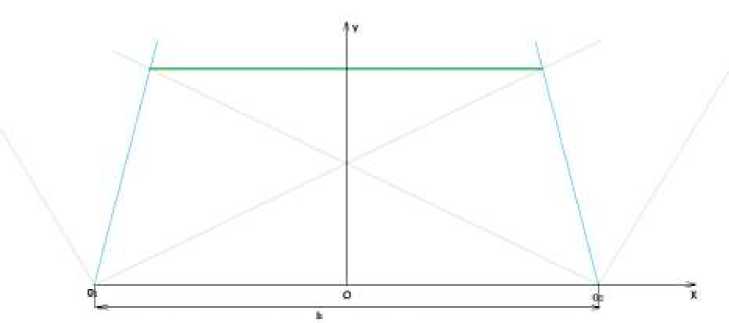
Рис. 1 – Схема зоны видимости камер (вид сверху).

Для расчета точного расположения траектории движения точки необходимо рассчитать углы обзора камер по формуле

а = 2arct g(—),                         (1)

где w =0,0055*2048 – горизонтальный размер матрицы в мм .

По результатам расчета прямая, задающая траекторию движения наблюдаемой точки, параллельна оси ОХ и описывается уравнением:

у = У * sinC180-^ ,

180-^

b*sin(—-)

У = sin(

При этом координата точки

X G [-b/2 + y * cos (180-p) ;b/2-y* cosC180-ф)].

3. Разрешающая система нелинейных уравнений

Согласно [1] пространственные координаты X и Y восстанавливаются по следующим формулам:

_     f^ X +X r ^b-^SlnP^

.

2((f2+X^Xr)sinф+fC0Sф(x^-Xr)) , b/2(C0S^ + 1) + 2/2(Xz—Xr)C0S^/2+bXzXr(C0S^-1)+4/XzXrSin^/2—b/(Xz-Xr)sin^ 2((f2+XlXr)sinф+fcosф(xl-xr))

Здесь xl и xr - абсциссы проекции наблюдаемой точки пространства на левую и правую матрицы стереопары, соответственно.

В рамках поставленной задачи необходимо, зная значения X и Y, найти координаты x l и x r , т.е. задача сводится к решению системы нелинейных уравнений относительно X и Y , заданных в (4).

После ряда математических преобразований система уравнений (4) приобретает следующий вид:

(axt + cxr + dxtxr + е = 0

{gxt + hxr + lxtxr + m = 0  '

где коэффициенты

a = 2Xfcosф + fb — 2f2sin ^/^,  с = —2Xfcosф — 2f2sin ^/^ + fb,

d = 2Xsin^; е = 2Xf2sin^, g = 2Yfcosф — 2f2cos^^ + bfsinф, h = —2Yfcosф + 2f2cos^/^ + bfsinф, l = 2Ysinф — bcosф + b — Afsin^/^,

m = 2Yf2sinф — bf2cosф — bf2.

При этом важно учесть, что рассматривается не одна точка пространства, а прямая траектория, т.е. полученная система должна решаться многократно для большого набора точек траектории, взятых с определенным шагом.

Система (5) легко решается методом подстановки. Для этого из второго уравнения выразим произведение xl xr через xl и xr и подставим результат в первое уравнение. Затем из полученного линейного соотношения выразим xr через xl и снова подставим его во второе уравнение системы. Таким образом, мы получим квадратное уравнение относительно xl, корни которого являются координатами наблюдаемой точки на левой и правой матрицах стереопары, и, естественно, не должны выходить за пределы матриц. Каждый набор решений системы записывается в отдельный массив.

Предлагаемый подход реализован в среде инженерных расчетов Matlab и в программе на языка C++. Экспериментально установлено, что в обоих случаях необходимо все вычисления выполнять с двойной точностью.