Определение координаты стыка при электронно-лучевой сварке по информационным параметрам сигнала датчика стыка

Одной из основных задач, решаемых при построении автоматических систем наведения электронного луча на стык, является определение координаты стыка и величины ухода стыкового соединения. В основе всех методик определения координаты стыка лежит анализ и обработка статической характеристики, полученной при помощи датчика стыка, где в качестве датчика стыка может быть использован рентгеновский датчик или коллектор вторичных электронов. Статическая характеристика является одной из основных математических зависимостей, составляющих модель датчика. Она показывает зависи

импульс от стыка отделяется от постоянной составляющей, инвертируется и нормируется по амплитуде.

При невысоком уровне помех, когда амплитуда сиг-нала Н _с в 5-10 раз превышает амплитуду помехи, определение координаты стыка х не вызывает затруднений. В качестве информационного параметра обычно используют моду распределения х _макс функции сигнала, которой соответствует максимальное значение амплитуды сигнала от стыка (рис. 2).

мость амплитуды сигнала датчика стыка от места положения луча относительно стыка. Если центр координат, описывающих положение луча, совместить с осью стыка, а ось А 'расположить перпендикулярно оси стыка, то

для нормального распределения плотности тока луча на поверхности обрабатываемых деталей статическая характеристика описывается выражением [1]

J д = W

1 -

(1 — K s )

° x 22

0.5 h s     ⁽ x ^-Е x ⁾²

J e  ²™x dx

- 0,5 h s

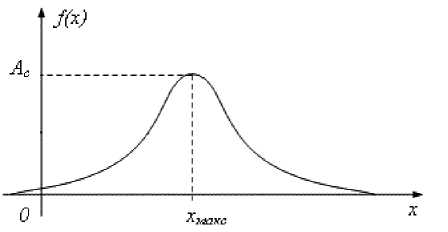
Рис. 2. Определение координаты стыка как моды распределения

где W - излучение с поверхности свариваемых деталей, £ - координаты математического ожидания электронов по осиА; о - среднее квадратическое отклонение электронов от центра пучка по оси А ; K _s - коэффициент, учитывающий неоднородность поверхности свариваемого изделия и наличие стыка; h - ширина зазора стыка.

На рис. 1 приведены статические характеристики, определяемые выражением (1) для различных отношений о Лу .

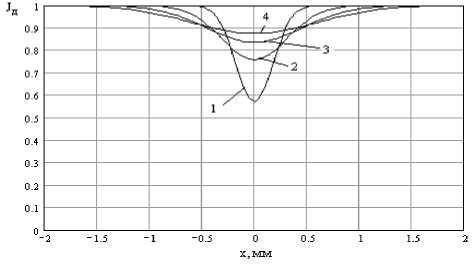
Рис. 1. Зависимость интенсивности рентгеновского излучения Л _д от места положения луча на стыке при h. = 0,3 мм; 1 - у yh_s = 0,5; 2 - у А.. = 1; 3 - у А.. = 1,5; 4 - у yh_s = 2

В большинстве устройств слежения за стыком для выделения информации сигнал датчика стыка подвергают обработке различными методами. Наиболее характерным для систем с поисковым сканированием является фазоимпульсный метод выделения сигнала [1]. При этом методе

Цля уменьшения вероятности пропуска сигнала в схеме управления устанавливают пороговый уровень обнаружения сигнала, равный 0,5-0,75 А , что приводит к возникновению методической погрешности определения координаты стыка.

Нестабильность основных технологических параметров электронно-лучевой сварки - ускоряющего напряжения, тока электронного луча, тока фокусирующей системы, наличие царапин и рисок вблизи стыкового соединения, уменьшение ширины зазора стыка, приводят к тому, что функция сигнала, полученная при помощи датчика стыка, может быть значительно искажена помехами (рис. 3).

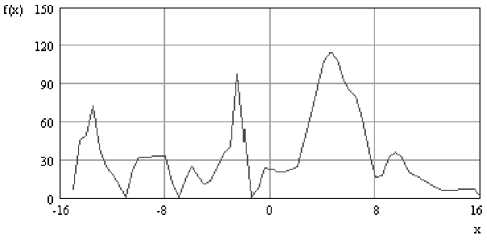
Рис. 3. Функция сигнала от стыка на фоне высокого уровня импульсных помех

В этом случае использование в качестве информационного параметра моды распределения приведет к ошибке в определении координаты стыка.

В качестве другого информационного параметра, устойчивого к различного рода импульсным помехам, может быть выбрана оценка в виде математического ожидания х _мо :

тс x „о = j xf (x) dx,                 (2)

—тс где/(х) - нормированная плотность распределения функции сигнала от стыка, условие нормирования задано в тс виде A j f (x) dx = 1.

Для дискретных отсчетов (рис. 4)

mn x„о =L x ^ ,             (3)

i=1     n где m - число интервалов разбиения функции сигнала от стыка по оси А'; Ax = xt — xi—1 - ширина интервала разбиения; п - число отсчетов датчика стыка в точке х; m n = ^ ni - объем выборки.

i = 1

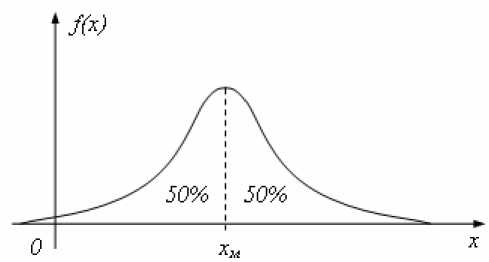
Рис. 5. Определение координаты стыка как центра симметрии распределения

Произведем оценку относительной эффективности определения координаты стыка при использовании в качестве оценки координаты стыка медианы распределения х _м и математического ожидания х . Дисперсия D найденной по выборке объемом п координаты любой квантили соответствующей вероятности ^ может быть определяем по формуле [5]

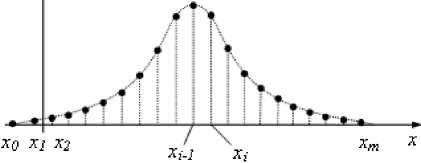
Рис. 4. Определение координаты стыка по дискретным отсчетам, полученным при помощи датчика стыка

D = Р ^{(1 —} P ) x p     n [ f ( x p )] ^{2 ,}

где х_р - координата квантили,/ (х ^ - плотность распределения в точке х_р .

Так для медианы_ р = 0,5, х _р = х _м . Дисперсия

Dx =     ¹---y.

x « 4 n [ f ( x „ )] ² Например, для распределения Лапласа

Среднее квадратическое отклонение рассеяния оценки математического ожидания о^_о зависит от среднего квадратического отклонения разброса усредняемых отсчетов о _x функции распределения сигнала от стыка и объема выборки п :

f ^{( x} ) = Ae e о У 2

—

плотность в центре распределения при х = 0 f ( ^х* ) = Аг .

оу 2

о

x «о

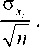
Достоинством данного метода определения коорди

наты стыка является то, что при усреднении одновременно уменьшаются все случайные погрешности вне зависимости от их происхождения. Однако существуют распределения, для которых математическое ожидание не может быть определено, например, распределение Коши. Оценка координаты стыка для такого распределения будет иметь большую погрешность.

Координата стыка может быть найдена как точка симметрии, которая делит площадь, ограниченную кривой /(х) нормированной плотности распределения функции сигнала, пополам (рис. 5). Эта точка называется 50 %-й квантилью распределения, или медианой х , и определяется выражением x« j f (x)dx = 0,5 . (5) —тс

Положительными аргументами в пользу данного метода определения координаты стыка является то, что понятие центра симметрии существует для всех видов распределений и оценка координаты стыка как медианы х является устойчивой к помехам в виде случайных выбросов.

Отсюда дисперсия рассеяния оценки центра в виде медианы для распределения Лапласа

D. = £, ^x “ 2 n

(Ю)

где о = о x i .

Сопоставляя дисперсию оценки координаты стыка в виде медианы и в виде математического ожидания, при одинаковом объеме выборке п получаем, что оценка координаты стыка медианой в два раза эффективней оценки в виде математического ожидания

D

E = ^: = 2.

Dx«     ,

где Е - относительная эффективность. Для нормального распределения

f ( x ) =

e ол! 2 я

-

, 2а2

плотность в центре распределения при х = 0

f ⁽ x м ) =

о У 2 я

.

В этом случае дисперсия рассеяния оценки центра в виде медианы

D = — ^x “     2 n

.

Относительная эффективность

D x „„ D x ,

E =

- = 0,64 . Л

Таким образом, для нормального распределения эффективность оценки х меньше чем х .

В общем случае для класса экспоненциальных распределений, задаваемых аналитическим выражением вида f (x) = Ae-x ,

где а - показатель степени распределения, относительная эффективность оценки координаты стыка медианой по сравнению с математическим ожиданием может быть определена как [4]

а ² Г (3/а)

[Г(1/а)]3 , где Г(г) - гамма-функция.

Для распределений с эксцессом г от 3 до 8 может выражение (17) быть аппроксимировано с погрешностью 5-10 % функцией вида

E = 0,12s ¹'⁶ ,

где г = Д ₄ /о ⁴ , Д ₄ - четвертый центральный момент распределения.

Следует отметить, что при снятии островершинных распределений дискретные отсчеты датчика стыка в центре распределения располагаются более плотно, в связи с этим медиана определяется более четко. У плосковершинных распределений отсчеты в центре распределения располагаются редко, и неопределенность медианы рез ко возрастает.

У симметричных двухмодальных распределений отсчеты группируются наиболее плотно в районе 25 %-й и 75 %-й квантилей - так называемых сгибов распределения (рис. 6). В результате этого для двухмодальных распределений с наименьшей дисперсией определяются координаты сгибов. Следовательно, для таких распределений наиболее эффективной будет оценка координаты стыка, определяемая как центр сгибов х _цс :

x 0,25 + x 0,75

x цс =-----2----- ,

где х _{0 25} - координата 25 %-й квантили, х _{0 75} - координата 75 %-й квантили распределения.

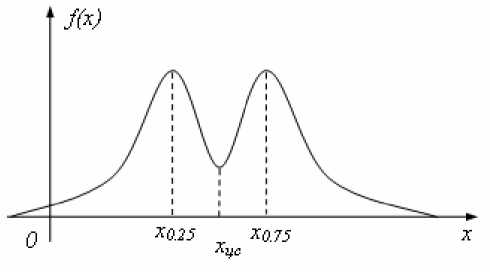
Рис. 6. Определение координаты стыка как центра сгибов распределения

Сопоставляя различные оценки определения координаты стыка, необходимо, кроме их эффективности, учитывать чувствительность этих оценок к действию различного рода помех. Ошибка в определении координаты сты ка зависит от координаты возможного искажения сигнала датчика стыка. С этой точки зрения оценка координаты стыка в виде математического ожидания хмо слабо защищена от влияния помех - влияние помехи ослабляется лишь в 4п раз. Квантильные оценки, напротив, являются защищенными от влияния побочных помех. Понижающей точность квантильных оценок, применение в методике обработки сигнала датчика стыка группирования дискретных отсчетов внутри интервалов разбиения Ах. Это приводит к возникновению постоянной составляющей со случайной амплитудой и ошибки в определении координаты стыка (рис. 7).

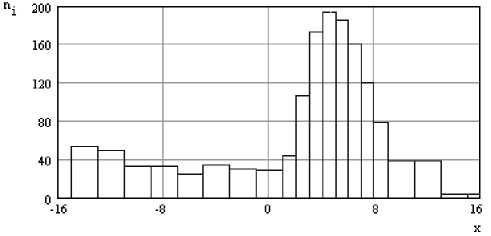
Рис. 7. Оптимальное группирование дискретных отсчетов датчика стыка

Защищенность квантильных оценок от импульсных помех возможно сочетать с уточнением среднего арифметического при увеличении объема выборки п , т.е. использовать смешанный метод определения координаты стыка как среднего арифметического 50 % центральных наблюдений х _{са0 5} . Центральными считаются отсчеты, лежащие на интервале между 25 %-й и 75-й квантилями:

^x 0,75

x са0,5 = j x^f ( x ) dx .                (20)

^x 0,25

Таким образом, несмотря на разнообразие методик оценки центра распределения, ни одна из них не может быть рекомендована в качестве универсальной по следующей причине - различные оценки имеют разную эффективность для различных видов распределений и помех. В условиях, когда еще нет данных о виде распределения и нет возможности выбрать наиболее эффективную оценку координаты стыка, можно рационально вычислить все пять оценок ( х _м , х _мо , х , х _{са0 5} и х _макс ) и за оценку координаты стыка принять оценку х , занявшую медианное положение в вариационном ряду, составленном из предыдущих оценок. Такую оценку можно считать достаточно эффективной, инвариантной к форме распределения и защищенной от помех.

Так, для приведенной статической характеристики (рис. 3) получаются следующие значения оценок центра распределения:

x м = 4; x мо = ²; x _цс = ²; x сао,5 = 3; x макс = 5;       ⁽²¹⁾

x ср = ³

Получаем, что координата стыка равна 3.

Выводы:

• 1.    Координата смыка может быть определена по информационным параметрам, вычисляемым по нормированной плотности распределения функции сигнала от стыка. В качестве информационных параметров может

• 2.    Эффективность использования информационных параметров зависит от формы распределения и устойчивости к действию помех. Наложение слабо меняющейся в процессе измерения помехи приводит к смещению квантильных оценок, основанных на вычислении соотношения площадей, ограниченных кривой плотности. Импульсные помехи оказывают влияние на информационные параметры, использующие для расчета амплитуду сигнала.

• 3.    В условиях, когда нет возможности выбрать наиболее эффективную оценку координаты стыка, рациональнее вычислить все пять информационных параметров - х _м , х _мо , х _цс , х _са05 и х _макс , и за координату стыка принять

быть выбрана мода распределения х _макс , математическое ожидание распределения х , медиана распределения х , центр сгибов распределения х _цс или среднее арифметическое 50 % центральных наблюдений.

оценку х , являющуюся медианой вариационного ряда, составленного из всех предыдущих оценок.