Определение координаты волокнистой частицы при нанесении на поверхность – основу

Перемещение твердых ворсовых частиц в технологии аэродинамического напыления осуществляется силой давления сжатого воздуха.[1] Процесс перемещения ворсинок важен не только как транспортировка их от бункера к основе, но и как подготовка к внедрению ворсинок в слой клея, в котором после сушки происходит закрепление ворса.

Волокнистые частицы, подаваемые из бункера, увлекаются потоком сжатого воздуха. При выходе из щели диффузора аэродинамического устройства частицы продолжают свое движение с начальной скоростью V 0 , при этом часть частиц совершает поступательное движение по траектории 1 (рис.1), другая же часть совершает комбинированное движение по траектории 2 (рис.1).

Рисунок 1 - Схема процесса напыления

Поступательное движение частицы описывается линейным дифференциальным уравнением:

— = 3 ⁿMv d э ( w — v ) dt m

где m - масса частицы, кг;

ц - коэффициент динамической вязкости воздушной среды, Па•с; d э - эквивалентный диаметр частицы, м;

W - средняя скорость воздушной среды, м/с;

V - абсолютная скорость частицы, м/с. [2]

3 ПЦ d3    _ 1   _

Заменяя выражение----— на — , получим dV dt

= 1(W - V ) , т

а в координатной форме дифференциальное уравнение (2) принимает вид:

dVx

<

dt dVy

I dt

= - ( Wx - Vx ) т

= ^- ( Wy - Vy ) т

Начальную скорость волокнистых частиц примем равной скорости истечения сжатого воздуха из сопла устройства. Для ее определения воспользуемся формулой Сен-Венана:

V 0

2 g ^k RT

⁵ к - 1

к - 1

' Р 2 ) ”

1 -

I Р1 J

где V 0 - начальная скорость истечения, м/сек;

R - газовая постоянная, для воздуха равная 287 Дж/(кг•град);

T - температура воздуха при истечении, равная 293 К;

к - показатель адиабаты расширения, для воздуха равный 1,4;

Р1 - давление перед соплом, Па;

Р 2 - давление во внешней среде, Па.[3]

Для определения координаты частиц, обладающих начальной скоростью при выходе из щели диффузора V0x — V0cosa и V0у — V0sina, решим систему дифференциальных уравнений (3), учитывая при этом, что движение происходит в покоящейся среде (W — 0), при отсутствии каких-либо иных сил, кроме аэродинамического сопротивления.

dVx 1 dt - TV 0 x   . dVy     1 „ , =     V 0 y I dt       т

i Vx t            ,                t In = Vx т         Vx — Vx • e T T-               ,             1             0         , .            (5) Vy t                            t In— = --        Vy — Vy • e T V 0 У      т          1       0

Решив систему уравнений (5), получим выражения для координат частицы в пространстве:

Г      -1-кX — V0 x • т 1 - e т

к

t к

т

Y — Vо у • к -к

нелинейным

Комбинированное движение частицы описывается дифференциальным уравнением:

V,— = 1 (w - V2)

0 dt т ' '

В предположении, что движение частиц происходит в покоящейся среде ( W — 0 ), при отсутствии каких-либо иных внешних сил, кроме аэродинамического сопротивления, уравнение (7) примет вид

dV 1 V 2

--=--- dt т V 0

Запишем выражение (8) в координатной форме и проинтегрируем:

' dV X	2 VX	dV X	dt		r "	1	t
dt	— т V 0 cos a	V X	т • V 0 cos a			V x	т • V 0 cos a
dV Y	L 1     VY"     ’	dVY	_       dt ,	L	_	1 =	t         .(9)
^ dt	= т V 0 sin a	. V Y	т • V 0 sin a		[	V y	т • V 0 sin a

dX	dY
Зная, что Vx —      и X dt	VY —     , получим dt

dt dX L X

— =------- ln t —------- t   tV0 cos a            tV0 cos а dt dY , L Y ,             (10)

- = „ .         ln t = „ . t    tV0 sin a       [      tV0 sin a

Окончательно получили следующее выражение для определения координат волокнистой частицы в пространстве:

f x

<

= ln t • т • V 0 cos a

Y = ln t • т • V 0 sin a

Полученные математические модели позволяют определить координаты положения твердой частицы на полотне – основе в результате аэродинамического напыления.

С целью проверки полученных теоретических моделей проведен эксперимент по определению положения частицы волокнистого материала при ее поступательном движении.

Экспериментально координаты частицы определялись промером расстояния, на которое переместилась частица, вылетевшая из сопла аэродинамического устройства. При проведении эксперимента изменялись параметры положения сопла относительно плоскости (300 и 600) и избыточное давление, подаваемое в аэродинамическое устройство (1000 Па, 2000 Па, 3000 Па). Положение частицы фиксировалось на плоскости с помощью координатной сетки. В таблице 1 сведены результаты эксперимента, а на рисунке 2 представлены графики зависимостей положения частицы на системе координат от угла атаки и скорости напыления.

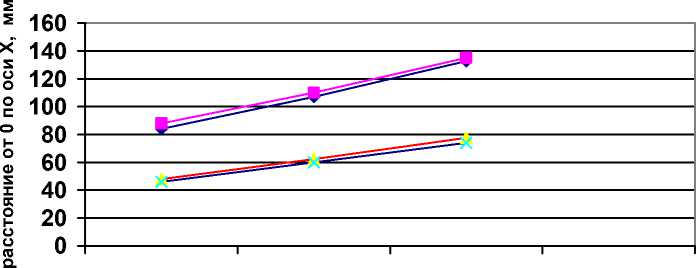
1000        2000        3000

давление, подаваемое в аэродинамическое устройство, Па

30 град теор 30 град эксп 60 град теор 60 град эксп

Таблица 2 - Результаты эксперимента

Угол атаки		Избыточное давление, подаваемое в аэродинамическое устройство, Па
		1000	2000	3000
Положение частицы по оси Х, мм
300	Теоретически	84	107	132,7
	Экспериментально	88	110	135
600	Теоретически	48	62,27	77,6
	Экспериментально	46	60	74

Рисунок 2 – Теоретические и экспериментальные зависимости положения частицы на полотне-основе

Отклонения значений, полученных экспериментально, от расчетных не превышает 5%, что дает возможность использовать полученные математические модели для определения различных параметров аэродинамического процесса. Разработанные теоретические модели позволяют определять параметры процесса напыления коротких волокон на основу, обеспечивая при этом качественные показатели многослойного текстильного материала.