Определение критических напряжений потери устойчивости для короткого стержня коробчатого сечения из упругопластического материала

¹ Несущая способность опорных кронштейнов ракеты-носителя «Космос-3М» определяется сечениями, представляющими замкнутую прямоугольную коробку. Материал кронштейна – литейный алюминиевый сплав АЛ23-1. Проведенные эксперименты показали, что потеря устойчивости происходит, когда материал кронштейна работает в упругопластической стадии деформирования.

В качестве расчетной схемы может быть принят короткий стержень коробчатого сечения в условиях внецентренного сжатия при следующих предположениях:

• -    напряжения во всех точках сечения превосходят предел упругости;

• -    потеря устойчивости происходит при увеличении сжимающей нагрузки, то есть в сечении отсутствуют зоны разгрузки;

• -    диаграмма σ _i (ε _i ) совпадает с диаграммой σ(ε);

• -    до потери устойчивости для сечения в целом справедлива гипотеза Гирхгофа-Лява.

Критические напряжения потери устой- чивости находятся из условия минимума потенциальной энергии системы с использованием уравнения Эйлера вариационной задачи [1]

аг d ( аг) d- Г аг) , -----7 ^-- Т --~ — 0. а^ dx\^ J dxAd^ J

■J ИССЛЕДОВАНИЯ

ПАуКО-Ж ГРАДА

Омин

Рис. 1

где Г - потенциальная энергия на единицу длины системы вдоль оси Х (рис. 1).

Грани стержня рассматриваются как пластины:

• -    в плоскости, параллельной XOY , - а х b х h 1 ;

• -    в плоскости, параллельной XOZ , - а х bхh 2 .

Потенциальная энергия элементарного участка dx может быть представлена в виде

Г = Г + Г2,               (2)

Для упругопластической зоны по теории

деформации при р = 0,5 значения изгибающих

M^D <р_с-

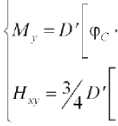
где

и крутящих моментов запишутся как [2]

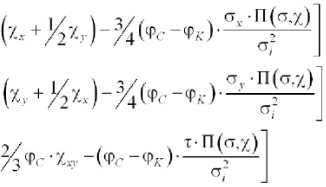
■ ² W

2 , Х У д 2W1 ду2 ,

где

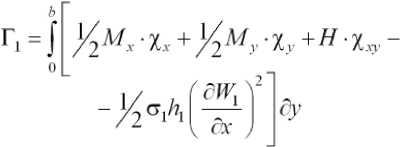
(2 ‘ )

χ

χ _xy

д ² W 1 ∂ x ∂ y

(3‘)

- потенциальная энергия элементарного участка dx пластины а х с (без учета влияния поперечных сил);

для плоскости XOY .

Аналогичные выражения для Мх , Mz и Hxz могут быть записаны для плоскости XOZ , где

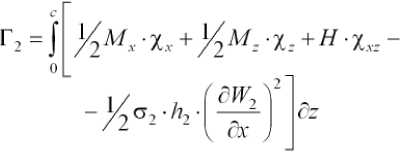
(2")

χ _x

-

д ² W ₂

дх 2

, X.

д 2W2 дz2 ,

χ

xz

д ² W₂ ∂ x ∂ z^.

- потенциальная энергия элементарного участка дх пластины а х с .

Принимаем, что до момента потери устойчивости в гранях стержня реализуется одноосное напряженное состояние.

Тогда

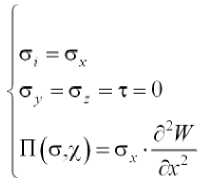
Подставив в систему (3) выражения (3 ' ) и (5), получим

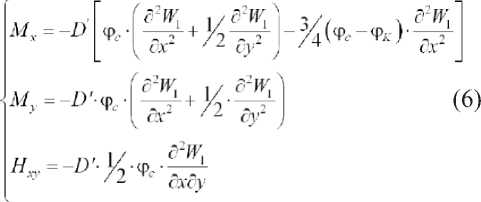
В системах (3) и (6)

Eh ³         E_CE_K

D ^— 9 ;    ^ф с = %; ^ф K = E; ;

E C — % - секущий модуль;

E _K

– касательный модуль.

Закон распределения напряжений по граням, параллельным плоскости ХОZ :

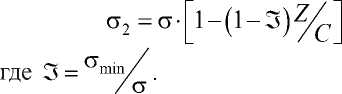
Учитывая эти обозначения, после подстановки (6) и (3 ' ) в выражения (2 ' ) и (2 " ) имеем:

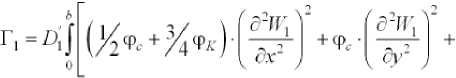
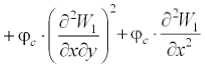
а^:ГГ, 1 + 3 ^ ( а²гН

V 2 о; (ar J

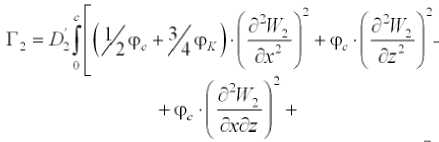
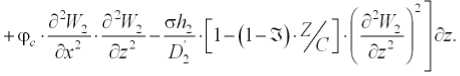
Функции прогибов пластин принимаем в виде

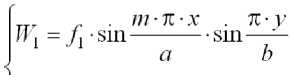
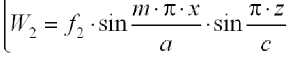
Условие равенства углов поворота по ребрам запишется как

S W j	= S W z
S y	S z y — 0	x — 0

(9 ' )

Тогда f2 = f1∙c/b.                     (10)

Введем обозначения:

т-т>х

/(л-) = /_Г8т------ а

Ду) = sm—^; о

(10 ' )

Тогда j (z) = sin----;

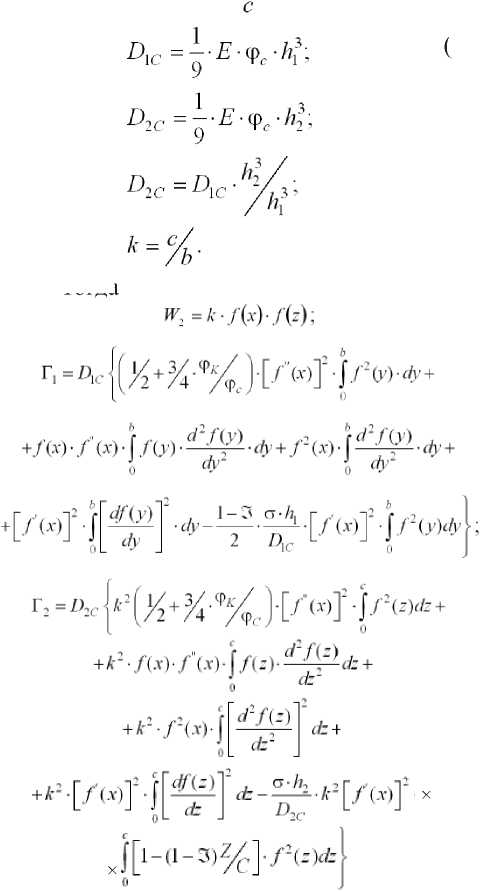
U ИССЛЕДОВАНИЯ

Havko-

Ж ГРАДА

Потенциальная энергия деформации элементарного участка стержня

EJ

f       d ² f ( y )

dy ²

dy + hУь^ • k ² • c f ( z ) d-JTz¹ • dz = / h 1     0        ^dz z

Г = D ie М f " ( x )]² • J f ²( y ) • dy +

_ 0

+ f ( x )• J '"( x ) J f ( y )•

+ hV

/i f

c

b

+

0 [

dy

• dy + ^

f df ⁽ y ) ²

^J 0 [ dy ]

^^ •_ j D _{1 C}

c

h ₂ ³

h 3 • k ² J f ²⁽ z ) dz ⁺

dZZy ) • dy + dy ²

d ^ f i z ! . dz dz ²

h3 k -J

h

• dy ⁺ 7h³

+

d² f ( z ) 1² dz ²

• dz

cc df ^{( z} ) ^{J [} dz

b

-Г- J ^f ^ y ) • dy ⁺

²   0

Здесь ф = 0,25 + 0,75^ K /ф.

+

1² . dz

^^^^e

Уравнение Эйлера (1) может быть преобразовано к виду

дГ d

дГ

d ²

дГ

дf ( x ) dx _9f '( x ) _]    dx _df "( x )_

= 0.

Найдя величины

дГ d

дГ

d2

дГ

df ( x ) ’ dx _ J ( x ) _] ’ dx ² _ дf ( x ) _]

из уравнения (12) с учетом (10 ‘ ) и подставив их в выражение (13), после некоторых преобразований получим уравнение

f'(x) + v • f"(x) + rf(x),

где

r =----- tXJ

•EJ;

v =

g^ h1

tEJ [ D1C

•EJ +XJ -XJ ;

2         4

;

XJ

f Г d² f ( y ) 0 _ dy y

2       ,3 / c Г dy + /v •k 2 J ' / h1     0 [

= j df ⁽ y ) ²

^J 0 [ dy ]

h 2/ /h

d² f ( z ) dz ²

dz =

4 ;

3 /       c dy + Jh3 •k2 •J '

/ ¹       0 ^[

J ( z ) 1 ² dz

dz =

2 ;

b

XJ =^ J ^{f 2(} y ) • dy ⁺

^{5          2}    0

c

4 • 1 h

1 — 5 n² + 1 ----

2      n²

Учитывая (10 ‘ ), уравнение (14) быть преобразовано к виду

Решением этого уравнения будет

D g = -JC. •л

где

а =

P =

Y =

^{3 3} / , 1 + h 713 • k ³

/ ^h 1

может

I •₽ + 2y ,(16)

b

XJ = J ^{f 2 (} y ) • dy ⁺

1            0

3 / c h7^ • k2 J f 2(z) • dz =

/ h 1      0

³ • h 2/ h

, 3 ;

1 +

+ k ² h 2

+5+ k³ h 2 2

+5+ k³ h 2

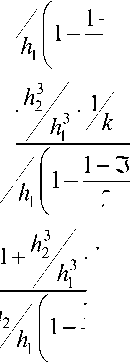
2      n ²

1 — 5 n ² + 1

• k

•

n ² + 1 n ²

•

n ² + 1 n ²

^ (17)

Обозначив m- = к , найдем минимум о:

d g   D_1C   2/

— = —1C •n / 7 • 2k • ф • а d к   h!   /Ъ2 [

^^^^M

4 •e = 0, к3

отсюда

X ⁴ =-^в-, ф-а

X 2

\ ф-а

1. Определяются к ; а 1 ; в 1 ; Y 1 при 3 = 1:

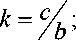
Подставив (19) в (17), получим

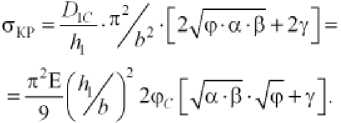
Таким образом,

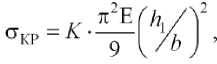
где K = 2 ф C ^д/ф-д/а-Р + yj , а, в, Y — величины, зависящие от соотношения геометрических параметров сечения ( K = c / b ; h ₂/ h ₁) и степени неравномерности загружения сечения 3 (17).

Введем коэффициент, учитывающий зависимость критических напряжений потери устойчивости от степени неравномерности загружения сечения 3 :

а 1	h 2        3 1+ /А3 k h 1
	1 + h 2Z - к3 h 1
в 1	h 2       1 = 1 + ./ h 1 3 /к .
	1 + h 2/- к3 ’ h 1
Y 1	h 2 3 _1 +,/ h , 3 к
	. 1 + h 2/ - к3 h 1

• 2.    Задаваясь значением по формуле (21) отношение рого это значение σ является

• 3.    По графику определяется σ_кр для конкретного b / h ₁.

Строится график σ_кр = f ( b / h ₁).

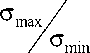
K с

2^

^С 3= 1

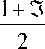
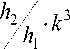
1 -3 п ² + 1

1 + hV^k^{3 3} h ₁

. (22)

Несущая способность стержня: при 3 = 1

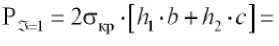
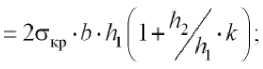
при 3 ^ 1

Р з, 1 = ^Р 3= 1

1 + 3

•--------------------------

.

2 - Kс

σ > σПЦ, найдем b h , для кото критическим.

Порядок расчета: исходные данные h ₁; h ₂; b ; c. Диаграмма сжатия σ _i = f (ε _i ).

• 5.    K _σ определяется по формуле (22).

• 6.    Запас устойчивости .

• 7.    Несущая способность определяется по формуле (23) или (24).

^а ' ®max

Используя вышеприведенные формулы, был проведен расчет для двух вариантов исполнения опорного кронштейна: из материалов АЛ23-1 и АЛ27-1 [3]. Принятые в расчете диаграммы σ(ε) приведены на рис. 2.

Геометрические параметры и величины, определяемые этими параметрами, по двум расчетным сечениям приведены в табл. 1.

Зависимости σ_кр от b / h для рассмотренных вариантов сечений и материалов приведены на рис. 3.

Несущая способность определяется сечением V и равна 83 т для АЛ23-1 и 80 т для АЛ27-1.

Таблица 1

Материал	Сечение	h 1, мм	h 2, мм	c , мм	b , мм	k	α	β	γ
АЛ27-1	IV	10	10	108	158	0,683	1	1,865	1,270
	V	10	10	80	108	0,740	1	1,670	1,235
АЛ23-1	IV	12	10	108	158	0,683	0,965	1,590	1,160
	V	12	10	80	108	0,740	0,958	1,445	1,130

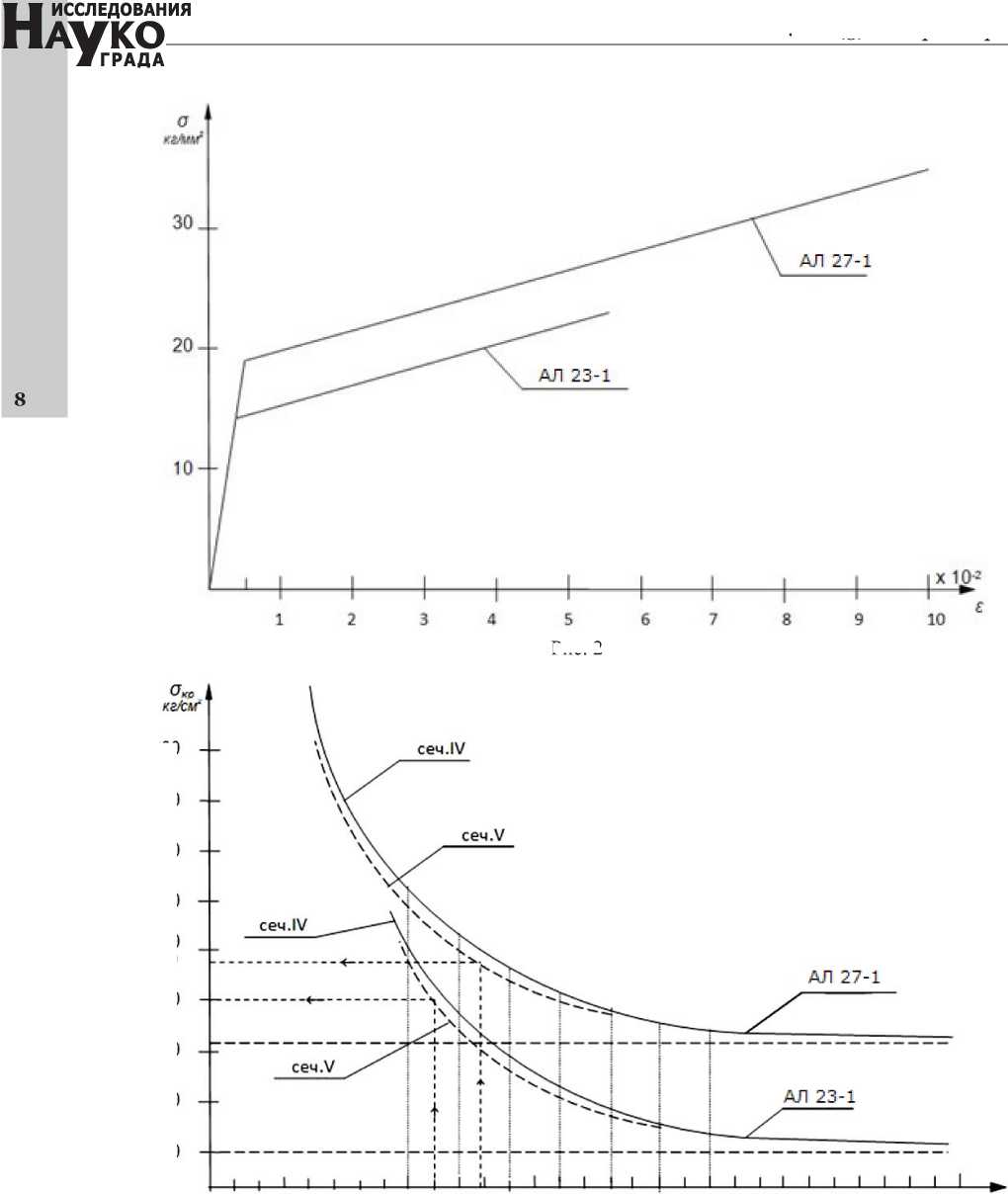
Рис. 2

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 b/h

Рис. 3

Экспериментальной проверке подвергались кронштейны из АЛ23-1.

Несущая способность этих кронштейнов была в пределах 85–100 т. Превышение экспериментальных значений несущей способности над расчетными объясняется проведением расчетов по минимальным толщинам.