Определение линейного размера объекта на изображении

Использование камеры в составе системы технического зрения для решения практических задач основано на формировании цифрового изображения исследуемого объекта и последующей его обработки. Формирование изображений по сути есть проецирование трехмерного в двумерное пространство, влекущее за собой серьезную потерю информации о геометрии наблюдаемой сцены. Реконструкция трехмерного пространства может быть выполнена на основе известных геометрических моделей оптической системы [1], позволяющих решать измерительные задачи: определение расстояния до объекта, истинных размеров объекта и т.д.

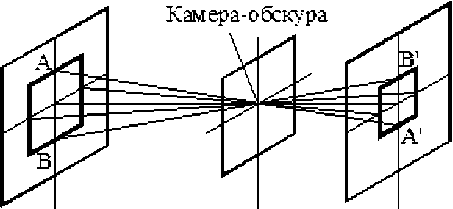
Основные геометрические аспекты формирования цифровых изображений оптической системой хорошо моделируются с помощью камеры-обскуры [1].

Изображение формируется с помощью бесконечно малого отверстия на фокальной плоскости. На рисунке 1 показано перспективное проецирование объекта при параллельном расположении плоскостей объекта и изображения, H – расстояние между объектом и камерой, f – фокусное расстояние камеры. Прямая АВ, принадлежащая плоскости объекта, проецируется на плоскость изображения в прямую B'A'.

н           f

Пло ско ль                   Пло сколь объекта                     изображения

Рис. 1. Геометрическая модель камеры-обскуры

Модель камеры-обскуры является чрезмерным упрощением системы формирования изображения. Геометрию даже для очень сложных оптических систем можно моделировать незначительной модификацией перспективной проекции [1-4].

Фокальная плоскость заменяется двумя главными плоскостями, которые пересекают оптическую ось в главных точках P 1 и P 2 (рис. 2).

Луч, направленный к первой главной точке, после прохождения через оптическую систему возникает из второй главной точки без углового отклонения. Расстояние между главными плоскостями P 1 и P 2 моделирует осевую протяженность оптической системы. Обозначения H и f соответствуют обозначениям на рисунке 1. Точки F 1 , F 2 – фокальные точки. Прямая АВ, принадлежащая плоскости объекта, находится на расстоянии H перед точкой F 1 . Плоскость изображения с расположенной на ней проекцией B'A' находится на расстоянии h за точкой F 2 . Геометрическая модель реальной оптической системы соответствует известным формулам Ньютона и Гаусса [1] для уравнения изображения. Соотношение между расстоянием до объекта, фокусным расстоянием и расстоянием до изображения становится очень простым.

Для практических целей можно использовать обе геометрические модели. Выбор модели будет зависеть от требуемой точности решения задачи реконструкции.

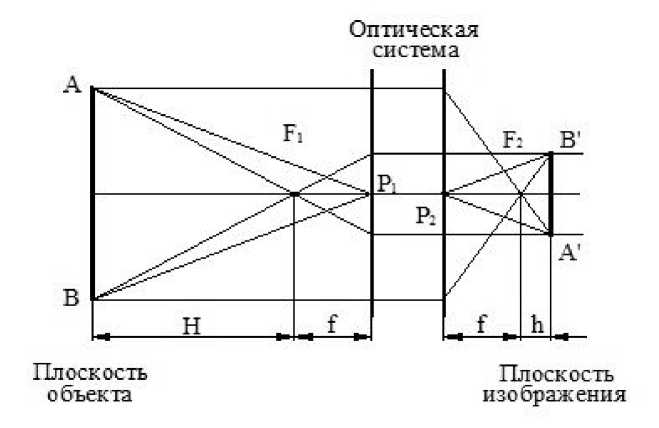
Рис. 2. Геометрическая модель реальной камеры

Обработка цифровых изображений заключается в выделении исследуемого объекта на изображении, определении его размеров в пиксельной системе координат. Далее необходимо определить метрические размеры изображения объекта, необходимые для решения задачи реконструкции трехмерного пространства. Очевидно, что для этого необходимо размер изображения объекта в пикселях умножить на физический размер одного пикселя и на поправочный коэффициент, учитывающий размер изображений.

Известно, что при формировании цифрового изображения изменение размеров изображения ведет к изменению размеров его составляющих пикселей. При максимальных размерах формируемого изображения количество пикселей изображения стремится к количеству эффективных пикселей камеры. Один пиксель изображения по размерам будет равен физическому размеру одного датчика-пикселя матрицы камеры. Тогда поправочный коэффициент, учитывающий размер изображения, для его максимальных значений равен единице. С уменьшением размера изображения значение поправочного коэффициента будет увеличиваться обратно пропорционально его размерам, т.е. будет определяться как отношение максимально допустимого размера изображения к фактическим его размерам.

Для использованной автором камеры Sony DSC-H50 максимальный размер изображения 3456x2592, дополнительные размеры 3456x2304, 3456x1944, 2592x1944, 2048x1536, 1920x1080, 640x480 [5-7]. В таблице приведены значения поправочного коэффициента по длине и по ширине для всех возможных размеров изображения.

Таблица

Значения поправочного коэффициента, учитывающего размер изображения

Метрические линейные размеры объекта, снятого камерой в одинаковых условиях съемки, но при разных размерах изображений на цифровом изображении, должны быть равны. Были сформированы цифровые изображения объекта протяженностью 150 мм двух разных размеров: 640х480 и 2048х1536, при прочих равных условиях съемки. Фрагменты цифровых изображений показаны на рисунке 3. Линейные размеры изображений в пикселях равны соответственно 35,3 и 113,4; поправочные коэффициенты – 5,4 и 1,69. Физический размер одного датчика-пикселя матрицы камеры равен 0,00166 мм. Тогда метрические линейные размеры будут соответственно равны 0,316 и 0,318 мм. Разница между вычисленными значениями небольшая – 0,002 мм.

Рис. 3. Фрагменты цифровых изображений исследуемого объекта: а – размер изображения 640х480; б – размер изображения 2048х1536

Для проверки корректности разработанного метода расчета метрического размера объекта на изображении была проведена серия экспериментов. Известны линейный размер объекта в предметной плоскости, расстояние между исследуемым объектом и плоскостью изображения. Определялись линейные размеры объекта на изображении в пикселях и миллиметрах, расстояние между исследуемым объектом и плоскостью изображения на основе геометрической модели реальной камеры. Погрешность расчета определялась как разность рассчитанного и фактического расстояний. Относительная средняя погрешность расчетов составила ≈ 0,8%. В целом результаты свидетельствуют о корректности разработанного метода расчета метрического размера объекта на изображении.