Определение линейных характеристик опорных узлов ротора под нагрузкой

УДК 534:62–13                                              

Funding information: the research is done on theme no. 10.4798.2017/БЧ within the frame of the government task of RF Ministry of Education and Science in R&D

Введение. Технический прогресс предъявляет новые, более высокие требования к качеству продукции машиностроения. Главным образом речь идет о высокой надежности, долговечности машин, их продуктивности и безопасности. Все эти параметры должны быть учтены и рассчитаны на этапе разработки.

С точки зрения производственных процессов особое значение имеет динамическое роторное оборудование, обеспечивающее непрерывность технологического процесса [1–3]. В [4] представлены схемы конструкций и принцип работы различных роторных машин, выполнен патентный поиск по каждому их виду. В [5] рассмотрен характер зависимости эквивалентной жесткости от частоты колебаний для определенной модели, приведена зависимость критических частот от эквивалентной жесткости опор. В [6] авторы подробно рассматривают вопросы контроля вибрации, виброналадочных работ и предотвращения увеличения вибрации роторных машин, равновесия роторов. Кроме того, здесь перечислены источники вибрации и приводятся базовые сведения из теории колебаний. В работах [7–9] обсуждаются проблемы динамики жесткого неуравновешенного ротора с четырьмя степенями свободы. Исследование [10] базируется на допущении, что реакции подшипника — это квазилинейные силы с кубической нелинейностью. С учетом этого рассматривается воздействие радиального зазора на движение в пространстве динамически неуравновешенного ротора под влиянием сил внутреннего трения. В [11] показаны взаимосвязи поперечных и крутильных колебаний, возникающие при вращении ротора центрифуги. Разработана линеаризованная математическая модель ротора в упругих опорах, учитывающая влияние поперечных и крутильных колебаний.

Проведенный обзор литературы позволяет утверждать, что исследование колебательного процесса и соответствующих параметров линейных механических систем представляет интерес. В данной работе рассмотрен ротор, в частности его опорные узлы с зазорами. Цель исследования — определить значения под нагрузкой линейных эквивалентных жесткостных параметров названных узлов.

Материалы и методы. В качестве ротора использована динамическая модель, предусматривающая вращение в упругих опорах с зазорами (рис. 1).

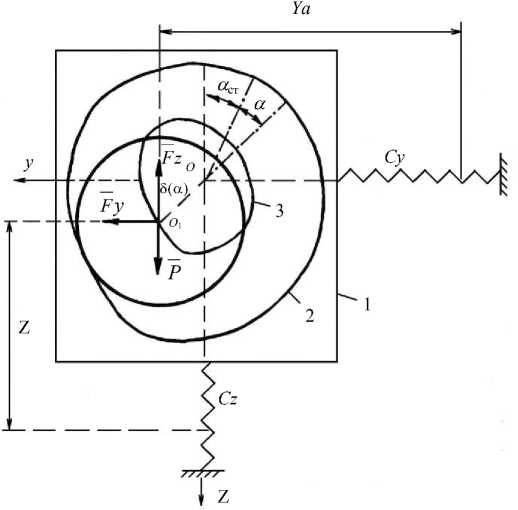
Рис. 1. Динамическая модель ротора, который вращается в упругих опорах с зазорами

На рис. 1 приняты следующие обозначения: 1 — опора ротора; 2 — граница контакта опоры с цапфой ротора; 3 — кривая относительного движения центра цапфы ротора; m — масса ротора; β (α) — радиальный зазор в роторных опорах (представлен функцией угла смещения его цапф от вертикальных направляющих); C y , C z — общие жесткости кожухов опорных узлов соответственно в горизонтальных и вертикальных направляющих; y _ст z _ст — статический сдвиг центра масс ротора в горизонтальном и вертикальном направлении, вызванный деформациями в опорных узлах; α — динамический угол наклона цапф ротора; α_ст — угол наклона от положения равновесия, вызванный технологической нагрузкой на ротор; y _α, z _α — полные динамические смещения центра масс ротора в указанных выше направлениях; f = Fz / Fy — взаимосвязь вертикальной и горизонтальной компонент технологической нагрузки.

Для определения потенциальной ( П ) и кинетической ( Т ) энергий исследуемой системы воспользуемся следующими равенствами:

П = 2 CyУ [Уа + Уст - 8 (“ + “ст ) sin (“ + “ст ) + 5 (“ст ) sin “ст ]2 +

+ 2 Cz [Za + Zст - 8 (a + «ст ) cos (a + aст ) + 8 (аст ) COs aст ]" -

-mg [Za + z- + 8 (аст ) COs аст ] >'

T = 2 m ( ^у 2 ⁺ z ² ) ⁺ 2 A ® ² .

Здесь A — полярный момент инерции, ® — угловая скорость вращающегося ротора.

Следует учитывать, что действующие силы не являются потенциальными. При этом обобщенные силы, которым соответствуют введенные ранее координаты y _α, z _α, α, примут вид:

Q y. = F y , Q a =- F ,

Q   F [8(a + a ст) cos (a + a ст ) + 5'(a + a ст) sin (a + a ст )] +

“ ^У [ ^{+ f} [ ⁸ ( ^{a + a} ст ) ^Sin ( ^{a + a} ст ) ^-8 ' ( ^{a + a} ст ) ^COS ( ^{a + a} ст ) ]

F

— взаимосвязь вертикальной и гори-

Здесь 8 (a + a ) — производная радиального зазора по углу a ; f = - ст                                                           Fy зонтальной компонент технологической нагрузки.

При данных условиях уравнения, выражающие динамику системы, можно записать: m^y a ^{+ C} y • У . — ^C y ⁸ ( ^{a + a} ст ) ^Sin ( ^{a + a} ст ) ^{+ C}y ⁸ ( ^a ст ) ^Sin ^a ст = ⁰, mza ^{+ C} z • z a ^{- C} z ⁸ ( ^{a + a} ст ) ^COS ( ^{a + a} ст ) ^{+ C} z ⁸ ( ^a ст ) ^{COS a} ст = ⁰, mg [ ⁸ ( ^a + ^a ст ) ^Sin ( ^{a +} “ ст ) ^{- 8} ' ( ^{a + a} ст ) ^COS ( ^{a + a} ст ) ] ^-

• ^{- С}y [ У а ^{- 8} ( ^{a + a} ст ) ^Sin ( ^{a + a} ст ) ^{+ 8} ( ^a ст ) ^Sin ^a ст ] ^X

• < ^X [ ⁸ ' ( ^{a + a} ст ) ^Sin ( ^{a + a} ст ) ^{+ 8} ( ^{a + a} ст ) ^COS ( ^{a + a} ст ) ] ^{+ + C} z [ z a ^{- 8} ( ^{a + a} ст ) ^COS ( « ^{+ a} ст ) ^{+ 8} ( ^a ст ) ^{COS a} ст ] ^X X[ ⁸ ( ^{a + a} ст ) ^Siⁿ ( ^{a + a} ст ) ^-8 ' ( ^{a + a} ст ) ^COS ( ^{a + a} ст ) ] =

  
  

  Машиностроение и машиноведение

  
  

  = F y

  
  

[ ⁸ ( ^{a + a} ст ) ^COS ( ^{a + a} ст ) ^{+ 8} ( ^{a + a} ст ) ^Sin ( ^{a + a} ст ) ] ⁺

+ f [ ⁸ ( ^{a + a} ст ) ^Sin ( ^{a + a} ст ) ^-8 ( ^{a + a} ст ) ^COS ( ^{a + a} ст ) ]

Рассмотрев более детально третье уравнение системы (1), определим угол наклона a_{c m}, считая a = 0.

После преобразований в уравнениях (1) получим более простую систему:

y              yz ya     экв  ya     экв a     ,

z               zy a      экв a      экв  ya      .

Анализ уравнений (2) позволяет в первой аппроксимации значений рассматривать упругую опору с зазором как опору с линейными упругими характеристиками (и в горизонтальных, и в вертикальных направляющих):

y              yz                    z              zy y      экв ya      экв a , z      экв a      экв ya .

Здесь

y _Cy [ mg • r + cos3 a ст (9 + f • z • z 2 • C )]   z    Cz [ mg • r + cos3 a ст (6 + f • z-62 • Cy )]

^С экв =                         .                          , ^С экв =                         .                          ,

A                               A yz        zy экв      экв

C y C z cos ^{3 a} ст ^⁶ • ^z ( ^{6 +} f • ^z ) A

r = 52 (aст) + 2S'(acm)2 -S(aст )-8"(aст),

6 = 3 ( aст ) + 8'(aст )• tgaст , z = 5(aст )• tgaст - 3' ( aст ) , A = mg • r + cos3 a ст (6 + f • z )•( Cz • z2 + Cy •б2).

Результаты исследования. В системе (3) величины Cy , Cz , Cyz выражают эквивалентные характе- ристики жесткости опоры с зазором.

Чтобы получить зависимости эквивалентных характеристик жесткости нелинейной механической системы, воспользуемся разложением тригонометрических функций в системе (1), учитывая слагаемые более высокого порядка. Для определения необходимых величин укажем:

Уа = Ay • sin “1 t , za = Bz • cos “1 t , где Bz , Ay — амплитуда общего колебания ротора в вертикальных и горизонтальных направляющих соответ- ственно, m1 — частота колебаний.

Таким образом,

2п rm “J

CL = — I ^Фу ( У а , z a ) Sin “ 1 ^tdt ,

П A y 0

2 n

CL = "“H Ф ( У а , z a ) c^OS “ 1 tdt •

П B 0

Здесь Фу (ya, za), Фz (ya, za) — функции координат ya, za. Эти величины можно определить, обратившись к системе дифференциальных уравнений (1).

Решая систему уравнений (4) методами интегрирования, представим величины в виде:

C^y экв

C^z экв

Cy (mgr + Cz cos a ст ■ b • z 2 ) ! CycOs a ст ^V•6• b' ( C^ ' 62 • A^ + C ' z 2 • Bz ) A                                 8A3

Cz ( mgr + Cy cos a ст ■ Ь ^ ) Cz'cos a ст 'У' z • Ь' ( C2 • 62 ' AS + Cz • z 2 • Bz )

A                                  8 A ³

Здесь

Ь = COS2 aст (6 + f • z) ,

У = 3 (a ст ) + 33' (a ст ) tga ст - 33''(a ст ) - S'" (a ст ) tga ст , ^ = 3 (aст ) tgaст - 33' (aст ) - 33" (aст ) tgaст + 3"' (aст ) •

Анализируя (5), можно говорить о взаимозависимости не только между жесткостями корпусов в опорах ротора C_y , C_z , но и амплитуд A_y , B_z его общих колебаний.

Необходимо подчеркнуть, что жесткость Cyz выражается как взаимосвязь движений ротора в горизон- тальной и вертикальной плоскостях. В случае Gyze = 0 в системе (2) уравнения не будут связаны, что позволяет учесть все возможные варианты. Они перечислены ниже.

— При отсутствии изменений радиального зазора со временем и a _ст = 0 имеем C ^_Ke = C _z . Такой вариант характерен для холостого режима работы ротора. При этом радиальное смещение ротора по отношению к опоре в вертикальных направляющих является совсем небольшой величиной, хотя и более высокого порядка, чем смещение в горизонтальных направляющих.

— Если принять z = 0, то CzK6 = Cz. Данная ситуация свойственна радиальному перемещению ротора по отношению к опоре в окружении точки, через которую проходит горизонтальная касательная к траектории относительного движения центра цапфы.

— При нулевом значении величины радиального зазора в опорах имеем C ^^ = C _y и C^z_{3 Ke} = C _z .

— Если отсутствуют изменения радиального зазора и а _ст = 90 ° , то С^ = С . Это возможно, если ротор работает при технологической нагрузке с подобранным зазором, т. е. в горизонтальных направляющих радиальное смещение принимает малые значения по сравнению с вертикальным направлением.

— При 0 = 0 С^ = С_у . В данном случае радиальные смещения ротора имеют место в окрестности точки, через которую проходит вертикальная касательная к линии относительного движения центра цапфы.

— Возможно выполнение равенства 0 + f - z = 0 . Это справедливо в случае радиального смещения ротора по отношению к опоре в окружении такой точки, через которую проведена нормаль, совпадающая с линией действия результирующей сил F r и F b . В этом случае С^ = С и С ^ = C_z .

Рассмотрим характеристики ротора на упругих опорах, жесткости которых равны C^y , C^z . Обозна-

чим 8 — эксцентриситет ротора, го — его угловая скорость. Уравнения колебаний представим в виде системы:

my a + С кв • y_a = m -8-го ² sin го i t mz a + С²_жв - z_a = m - 8 - го ² cos го t

Решая (6), запишем выражения для амплитуд колебаний:

A y

2                              2

m-8-го           m-8-го

------------т, B7 =------------г .

С У, - m -го ² z   С^ - m -го ²

Заметим, что слагаемые C^y , C ^z в знаменателях зависят от амплитуд A_y , B_z . Представим графически

рассматриваемую систему (рис. 2).

го ²,( го у )²,( го z )²

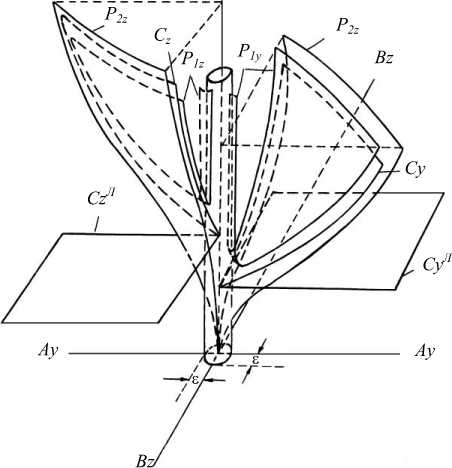
Рис. 2. Графическое представление динамических характеристик абсолютных колебаний ротора в опорах с зазорами

Поверхности P1y , P2y , P1z , P2z (резонансные) и Cy , Cz (скелетные) построены в предположении, что амплитуды Ay и Bz изменяются независимо на основании (7) и равенств Сув = m (гоу ) , СУв = m (гоZ) .

Амплитуды вынужденных колебаний A_y, B_z соответствуют частоте возмущающих сил го ₀. Принимая во внимание этот факт, для получения выражений указанных амплитуд сначала построим плоскость го ² = го 2 .

На линиях пересечения построенной плоскости с поверхностями P _{1 y} , P _{2 y} и P _{1 z} , P _{2 z} будут точки с идентичными координатами. Эти точки — искомые амплитуды колебаний ротора.

Плоскости C_y^Л , C_z^Л — скелетные поверхности линейной системы. В этом случае в выражениях для эквивалентных жесткостей берутся только первые слагаемые. Они указывают на то, что частоты свободных колебаний линейной системы не зависят от амплитуд.

Машиностроение и машиноведение

Резонансные поверхности представляют колебания ротора в горизонтальных направляющих, а скелетные — в вертикальных. Они построены в различных координатных октантах. По форме скелетные поверхности являются эллиптическими параболоидами. На рис. 2 ω cy , ω cz представляют собой частоты свободных колебаний системы.

Обсуждение и заключения. Одной частоте могут подходить несколько точек. Это означает, что в исследуемой системе возможно несколько режимов колебаний, в том числе неустойчивых. Для перехода системы с одного устойчивого режима движения на другой необходимы некоторые внешние воздействия, что характерно уже для нелинейных систем.

В качестве примера применения полученных зависимостей можно привести задачу о вынужденных колебаниях ротора вследствие его статической неуравновешенности.

Представленные в работе зависимости (4) указывают на то, что эквивалентные угловые жесткости взаимозависимы не только через жесткости C y , C z корпусов, но и через амплитуды A y , B z общих колебаний ротора.

В результате исследования линейных характеристик опорных узлов нагруженного ротора получены следующие результаты.

• 1.    Предложена динамическая модель ротора, вращающегося в упругих опорах с зазорами. Данная модель позволяет исследовать задачи определения линейных эквивалентных жесткостных характеристик опорных узлов.

• 2.    Проанализирована система уравнений и перечислены возможности применения формул. В частности, с их помощью можно определить колебания ротора в горизонтальной плоскости на строгальных машинах, используемых для получения заготовок кожи.