Определение массовой энергоемкости маховика гиперболического профиля



Правило 2 похоже на правило 1, только благодаря малой угловой скорости система управления прилагает большую положительную силу, что быстрее приводит систему к правилу 3.

Правила 4 и 5 говорят о том, что ничего делать не нужно, если система находится в этих состояниях. В правиле 4 маятник либо движется в желаемое состояние, либо покоится, поэтому можно ничего не предпринимать. В правиле 5, казалось бы, необходимо приложить положительную силу, однако это правило призывает не прикладывать силу. Дело в том, что в ситуации, когда у тележки скорость положительная, а угол отрицательный, вряд ли угловая скорость может быть равна нулю, поэтому данное правило либо срабатывает редко, либо не срабатывает вовсе.

Правило 6 напоминает правило 5, только угловая скорость положительна, и в такой ситуации система управления принимает правильное решение: приложить большую положительную силу.

Правила 7 и 8 заставляют маятник рывком двигаться к нулевому положению.

Построенная база правил не может быть признана совершенной, однако управление системой она выполняет эффективно. Кроме того, база может быть подвергнута анализу и корректировке специалистами.

Предложенный в данной статье подход является эффективным средством автоматического проектирования интеллектуальных информационных технологий, позво ляющим легко получать конкурентоспособный результат, сравнимый с результатом специалистов, не заменяя последних, а освобождая их для более продуктивной творческой работы. Применение этого подхода позволит существенно сократить затраты на разработку интеллектуальных технологий.

Работа выполнена при поддержке ФЦНТП по проек-там№2006-РИ-16.0/001 и2006-РИ-19.0/001/377.

Библиографический список

• 1.    Koza, J. R. Genetic programming tutorial [Электронный ресурс] / R. J. Koza. Электрон. дан. Режим доступа: http://www.genetic-programming.com/gpanimatedtuto-rial.html . Загл. с экрана.

• 2.    Koza, J. R. Hierarchical genetic algorithms operating on populations of computer programs / R. J. Koza // Proc. of the 11th Intern. Joint Conf. on Artificial Intelligence. San Mateo : Morgan Kaufman, 1989.

• 3.    Липинский Л. В. Подходы к формированию базы правил для нечетких систем управления / Л. В. Липинский, В. А. Малько // Вестн. Сиб. гос. аэрокосмич. ун-та им. акад. М. Ф. Решетнева / под ред. проф. Г. П. Белякова; Сиб. гос. аэрокосмич. ун-т Вып. 5. Красноярск, 2004. С. 83-90.

• 4.    Интеллектуальные технологии автоматизации проектирования системы управления на нечеткой логике: прогр. для ЭВМ / Л. В. Липинский, В. А. Малько, Е. С. Семенкин. М., 2006. Зарег. в ВНТИЦ, № 50200600369.

• L. V. Lipinsky, Е. S. Semenkin

APPLICATION OF GENETIC PROGRAMMING ALGORITHM IN AUTOMATED DESIGN OF INTELLECTUAL INFORMATION TECHNOLOGIES

Application of genetic programming approach in automated design of artificial neural networks and fuzzy logic controllers is described. Examples of real world problems solvingfrom wide area of decision support are given.

А. В. Лопатин, И. В. Макаров, М. А. Рутковская

ОПРЕДЕЛЕНИЕ МАССОВОЙ ЭНЕРГОЕМКОСТИ МАХОВИКА ГИПЕРБОЛИЧЕСКОГО ПРОФИЛЯ

Рассмотрена задача определения величины массовой энергоемкости маховика, профиль которого имеет форму гиперболы. Получено аналитическоерешениеуравнений, описывающих напряженное состояниемаховика при вращении. Выполнен анализ влияния на коэффициент формы маховика геометрических параметров диска. Приведено сравнение аналитических решений с решениями, полученными методом конечных элементов.

Маховики принадлежат к числу древнейших механизмов, способных накапливать энергию. В настоящее время существует множество маховичных систем аккумулирования энергии, используемых в различных областях техники [1]. В частности, маховики нашли применение на космических аппаратах в качестве накопителей энергии и устройств стабилизации.

Качество накопителя энергии оценивают величиной массовой энергоемкости, которая находится как отношение энергии, запасаемой на режиме предельно возможной угловой скорости, к массе маховика. Определение максимальной угловой скорости связано с решением задачи о распределении напряжений, возникающих во вращающемся маховике, от центробежных сил. Наибольшее распространение в технике получили маховики, симметричные относительно своей срединной плоскости. В таких маховиках реализуется двумерное осесимметричное напряженно-деформированное состояние, для расчета которого в общем случае можно использовать только численные методы - метод конечных разностей или метод конечных элементов.

Вместе с тем для расчета маховиков широко используется дисковая теория [1-3]. В соответствии с этой теорией симметричный маховик находится в плоском напряженном состоянии, при котором напряжения равномерно распределены по толщине. Использование дисковой теории возможно в том случае, когда толщина маховика мала по сравнению с диаметром и достаточно плавно изменяется вдоль радиуса. Предположение о плоском напряженном состоянии существенно упрощает расчет маховика. Разрешающие дифференциальные уравнения в дисковой теории являются обыкновенными: все искомые функции в них зависят только от радиуса. Дисковая теория позволяет получить аналитические решения уравнений, описывающих напряженное состояние маховиков определенного профиля [1; 2].

В данной статье рассматривается маховик гиперболического профиля. Задача о распределении напряжений в таком маховике решена достаточно давно [1; 2]. Однако задача определения массовой энергоемкости и коэффициента формы маховика с гиперболическим профилем до настоящего времени не имеет своего решения.

Рассмотрим маховик, вращающийся с угловой скоростью to вокруг оси ^ (рис. 1).

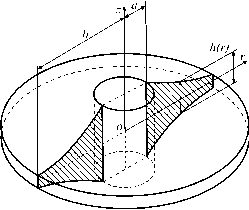
Рис. 1. Система координат маховика

Толщина маховика И является функцией радиуса г. Обозначим через а и b внутренний и внешний радиусы маховика соответственно. Система уравнений, описывающая напряженно-деформированное состояние маховика в рамках дисковой теории, включает уравнение равновесия dУ. + У .dh + У, - У. + .   r = а (!)

dr h dr r физические соотношения

У . = E ^(е . + ^МЕ , )> У r = E ^(е r + м^Ь         ⁽²⁾

геометрические соотношения

£

и

u

, £ r r du dr

В уравнениях (1).. .(3) о _г , <з ₆ - радиальное и окружное напряжения (рис. 2); £ _г , £₆ - радиальная и окружная деформации; и - радиальное перемещение; р - плотность материала; E = E /(1 - ц ²) ; Е - модуль упругости; ц - коэффициент Пуассона.

Получим разрешающее уравнение, содержащее в качестве неизвестного радиальное перемещение и. Для этого последовательно подставим физические (2) и геометрические (3) соотношения в уравнение равновесия (1). В результате преобразований имеем d2 и (1 dh 1 ^ du у +I---1—+ dr I h dr r J dr

1 ( m dh 1 ^

+ I — u += r I h dr r j E

Уравнение (4) представляет собой дифференциальное уравнение второго порядка с переменными коэффициентами и в общем случае может быть решено только численно.

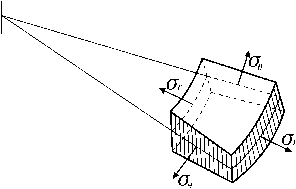
Рис. 2. Напряжения в маховике

Рассмотрим маховик, профиль которого имеет форму гиперболы

- n h = hb Ir                         (5)

I b J и допускает аналитическое решение уравнения (4). В уравнении (5) Иь - толщина маховика при г = b (рис. 3), н - параметр. Подставляя (5) в (4), получим d2 и 1 du

—- + ( 1 - n )— + dr ²    г ⁷ dr

1               cm ² r _

+ — ( 1 + n m ) u +—=— = 0.

r ²              E

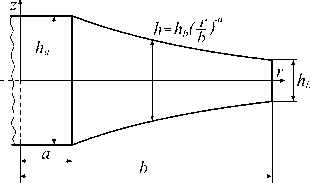
Рис. 3. Размеры маховика

Общее решение уравнения (6) имеет следующий вид cm2      1

u = —=--

E 8 - n (3 + м)

r ³ + C , r + C 2 r ^- t ,

где С ₁ и С ₂ - постоянные интегрирования;

- n + Jn ² + 4(1 + n м)      n + Jn ² + 4(1 + n m)

t =---------------------- ; s =--------------------. ⁽⁶⁾

2                     2

Получим выражения для напряжений О _г и а₆ . Подставляя (3) и (7) в равенства (2), имеем

У r = ^E

cm ²    3 + м ₂

-=--r ² +

E 8 - n (3 + m)

+ C r^s ^s + m) - C 2 r ⁽ t ⁺¹) ( t - m)

^^^^^^в

У и = E

сю ²   1 + 3м

E 8 - n (3 + м)

Ф е =

+ C 1 r^{5 - 1} (1 + 5 м) + C ₂ r ^{- ( 1 + 1)} (1 - 1 м)

Для определения постоянных интегрирования С ₁ и С ₂ воспользуемся граничными условиями, предполагающими отсутствие радиальных напряжений на внутреннем и внешнем радиусах:

г

-

х

3 +ц

х

8 - n (3 + ц )

₂ 1 + 3 ц     _$ч 1 + 5 ц 1 - с^{1 + 3} ^

а²----- + а ^{5 1}-----------+

3 + ц        5 + ц 1 - с ^{+ 1}

с 1 - 1 ц с⁵ - с ³

.

у r ( r = a ) = 0, У r ( r = b ⁾ = 0.

Подставляя (9) в (11), получим следующую систему алгебраических уравнений:

а^{5 - 1} ( 5 + м) C 1 - а ^{- 1 + 1)} ( 1 - м) х

^          а ^{1 + 1} 1 -ц 1 - с^{5 + 1}        ,

Безразмерные функции о _г и о _е задают форму распределения напряжений вдоль безразмерного радиуса маховика. Определим эквивалентное напряжение в маховике с помощью критерия Мизеса:

o =

'е^-° r ^О е .

„   сю ²   3 + м ₂

х C =              а ,

E 8 - n (3 + м)

b^{5 - 1} ( 5 + м) C 1 - b ^{- ( 1 + 1)} ( 1 - м) C ₂ =

_ сю ²   3 + м ь 2

= ПТ 8 - n (3 + м) .

Решая систему (12), найдем

Подставляя (16) в (18), получим о = р® ² b ² ф ,

где

Ф = 4ф ² +Ф е -

Ф r Ф е .

_ 3 + м сю

C 1 =       —

5 + м E

^{3 + м}

^C 2 = У

1 - м

8 - n (3 + м)

b^{1 + 3} b^{5 + 1}

^^^^^^s

-

а^{1 +3} а^{5 77,}

х аФ¹

СЮ 2

E b ³ a^s ь⁷⁷

х

8 - n (3 + м)

-

-

a ³ b а^{5 + 1}

.

Подставляя равенства (13) в выражения для напряжений (9) и (10), имеем

х| - r ²

(

- r ²

х

О _r = СЮ'

3 + м

х

b^{1 + 3} bF

- а

8 - к (3 + м)

, I + 3

-

а^{5 + 1}

- r ^-

’^{( 1 + 1)} аФ¹

b ³ a^s b^{5 + 1}

-

-

а ³ b⁵ "  а^{5 + 1}

,

У и = ^СЮ 2

1 + 3 м

3 + м

3 + м

8 - n (3 + м) . 1 1 + 5 м b^{1 +} 3

5 + м b^{5 + 1}

-

-

а1+3 ) + а5+1

-

( 1 + 1) ^{1 - 1 м} ФЬ^{1 b 3 а5}

1 - м       b^{5 + 1}

-

-

a ³ b а^{5 + 1}

.

Уравнения (14) задают распределение напряжений по радиусу маховика гиперболического профиля. Для удобства анализа полученных выражений (14) перейдем к безразмерной координате

б = r . b

Переменная а изменяется в пределах от с = а / b до 1. Учитывая равенство (15), запишем уравнения (14) в следующем виде:

у и = ^СЮ 2 b Ф е ^, у r = СЮ ² b ² ф_р ,

где

3 + ц ф =--------х r 8 - n (3+ц)

Г            1 - с ^{+ 3}

х -а ² + а ^{5 - 1}------

I                 1 - с^{5 + 1}

ctc

-

с ³ )

-

а ^{1 + 1} 1 - с^{5 + 1}

;

Определим максимальную угловую скорость, с которой может вращаться маховик, не разрушаясь. Для этого положим о = О _у , где о ^- напряжение текучести материала и затем определим ф = тах{ ф }. Тогда из (19) для квадрата частоты имеем

2         ^О У

® тах = ,2

Р ^b Ф тах

.

Значение максимальной угловой скорости может быть вычислено по формуле

f   /О”

®тах= marj  , b Р Р

где f = 1 /а/ф . max / v ^ф тах .

Как показывает анализ равенства (20), для маховиков, профиль которых допускает использование дисковой те-^оP^{ии, б} тах " ^б е ^{( а c}h ^т. ^е.

Ф тах

х

Г „2 1 + 3 ц - с--

3 + ц

3 + ц

х

8 - n (3 + ц )

5 - 1 1 + 5 ц 1 - с^{1 +} 3 J

5 + ц

1 - t ц с⁵-

1 - с

,5 + 1

.

- с

c

1 -ц 1 - С ^{+ 1}

Это обусловлено тем, что при а = с окружное напряжение О_е в маховиках с плавно меняющейся толщиной достигает своего максимума, а радиальное напряжение О равно нулю.

Определим массовую энергоемкость Q маховика как отношение кинематической энергии, запасаемой при вращении с максимальной угловой скоростью ® _тах к массе:

1 J

^Q = Д~® тах , 2 m

где J - момент инерции; т - масса маховика.

Массу и момент инерции маховика можно найти следующим образом:

b

b

J = 2 пр j hr ³ dr , m = 2 np j hrdr .

a

a

Подставляя (5) и (15) в (25), получим 2 Kp h₆b 3        _к +2

m 2 - n ^{( 1 с} ) ,

J =

₍ 1 _- c - n + 4 ₎ .

2 πρ h_bb ⁴ 4 - n

С учетом равенств (21) и (26) выражение для массо вой энергоемкости (24) примет следующий вид:

Q     K ,                  (28)

ρ где К коэффициент формы маховика с гиперболическим профилем,

1     2 - n 1 - c ^{- n + 4}

2 ϕ max    4 - n 1 - c ^{- n + 2} .

Коэффициент формы К зависит от геометрических параметров маховика и и с и характеризует степень совершенства конструкции. Выполним анализ влияния параметров и и с на коэффициент формы К. Определим диапазон изменения параметров и и с по условию равенства масс маховика с гиперболическим профилем и маховика с постоянной толщиной.

Перепишем выражение (26), определяющее массу маховика с гиперболическим профилем, в виде m = 2прhbb2 (i - xc2),              (30)

2-n где х = h/ hb - отношение толщин маховика на внутреннем и внешнем радиусах (см. рис. 3).

Масса маховика с постоянной толщиной т ₀ определяется следующим равенством:

m o =^ПР h o b ² ( 1 ^- c ² ) ,                 (31)

где h ₀ - толщина маховика.

Определим далее, как связаны между собой величины и, х и с. Полагая в формуле (5) h = ha при г = а, найдем ln x n=-   .

ln c

Приравнивая выражения (30) и (31) и учитывая соотношение (32), имеем ln x1 - xc2

2 +--2 п----^ = 0,             (33)

ln c 1 - c ²

где n ⁼ h /h ₀- отношение толщины маховика с гиперболическим профилем на внешнем радиусе к толщине маховика, профиль которого не меняется вдоль радиуса.

Выражение (33) представляет собой трансцендентное уравнение с неизвестным х. Задаваясь различными значениями сип можно, решая (33), определить параметр и, при котором массы двух рассматриваемых выше маховиков будут равны.

Пусть параметр с изменяется в пределах 0,1...0,2, а пара-метр п -в пределах0,85...0,95. Коэффициент Пуассона ц = 0,3.

Значения х = ha/ hb и параметра и представлены в табл. 1 и 2, значения бши и Уши, позволяющие оценить напряжения в маховике и максимальную угловую скорость, приведены в табл. 3, 4. Значения коэффициента формы К и отношения К / К0, где К0 коэффициент формы маховика с постоянной толщиной (и = 0),

К =---1 + c----

3 + ц+ c ²(1 -ц )

отражены в табл. 5 и 6. Как показывает анализ соотношения К / К ₀, маховик с гиперболическим профилем эффективней маховика, толщина которого постоянна. Это особенно заметно при малых значениях с и п .

Выполним далее анализ равенства (20) для рассматриваемых диапазонов изменения параметров с и п . Изменения функций ф/а ), ф_в ( а ) и ф ( а ) для с = 0,1,0,15,0,2 и П = 0,85,0,95 представлены на рис. 4.

Таблица 1

Значения параметра х
С	п
	0,850	0,875	0,900	0,925	0,950
0,10	2,083	1,840	1,627	1,439	1,274
0,11	2,033	1,804	1,601	1,422	1,264
0,12	1,990	1,772	1,578	1,407	1,255
0,13	1,952	1,743	1,558	1,393	1,247
0,14	1,918	1,718	1,539	1,381	1,239
0,15	1,887	1,694	1,523	1,369	1,232
0,16	1,859	1,673	1,508	1,359	1,226
0,17	1,834	1,654	1,494	1,350	1,221
0,18	1,810	1,637	1,481	1,341	1,215
0,19	1,789	1,620	1,469	1,333	1,210
0,20	1,769	1,605	1,458	1,326	1,206

Таблица 2

Значения параметра и

С	п
	0,850	0,875	0,900	0,925	0,950
0,10	0,319	0,265	0,211	0,158	0,105
0,11	0,322	0,267	0,213	0,160	0,106
0,12	0,325	0,270	0,215	0,161	0,107
0,13	0,328	0,272	0,217	0,163	0,108
0,14	0,331	0,275	0,219	0,164	0,109
0,15	0,335	0,278	0,222	0,166	0,110
0,16	0,338	0,281	0,224	0,167	0,111
0,17	0,342	0,284	0,226	0,169	0,112
0,18	0,346	0,287	0,229	0,171	0,114
0,19	0,350	0,291	0,232	0,173	0,115
0,20	0,354	0,294	0,234	0,175	0,116

Таблица 3

Значения параметра 6

max

С	п
	0,850	0,875	0,900	0,925	0,950
0,10	0,605	0,638	0,673	0,709	0,747
0,11	0,615	0,647	0,681	0,715	0,751
0,12	0,625	0,656	0,688	0,721	0,755
0,13	0,634	0,664	0,694	0,726	0,759
0,14	0,642	0,671	0,701	0,731	0,763
0,15	0,650	0,678	0,706	0,736	0,766
0,16	0,657	0,684	0,712	0,740	0,769
0,17	0,664	0,690	0,717	0,744	0,772
0,18	0,671	0,696	0,722	0,748	0,775
0,19	0,677	0,701	0,726	0,752	0,778
0,20	0,683	0,706	0,731	0,755	0,780

Графики (см. рис. 4) показывают, что фг равно нулю при а ^ с и а ^ I и достигает своего максимума внутри маховика. Максимальные значения функций фв и ф реа- лизуются всегда при а = с. Этим подтверждается справедливость равенства дшах = фв(а = с).

Таблица 4

Значения параметра f max

С	п
	0,850	0,875	0,900	0,925	0,950
0,10	1,286	1,252	1,219	1,187	1,157
0,11	1,275	1,243	1,212	1,182	1,154
0,12	1,265	1,235	1,206	1,178	1,151
0,13	1,256	1,228	1,200	1,173	1,148
0,14	1,248	1,221	1,195	1,169	1,145
0,15	1,241	1,215	1,190	1,166	1,143
0,16	1,234	1,209	1,185	1,162	1,140
0,17	1,227	1,204	1,181	1,159	1,138
0,18	1,221	1,199	1,177	1,156	1,136
0,19	1,216	1,194	1,173	1,153	1,134
0,20	1,210	1,190	1,170	1,151	1,132

Таблица 5

Коэффициент формы К

С	п
	0,850	0,875	0,900	0,925	0,950
0,10	0,386	0,371	0,356	0,343	0,330
0,11	0,380	0,366	0,353	0,341	0,329
0,12	0,375	0,363	0,351	0,339	0,328
0,13	0,371	0,360	0,348	0,337	0,327
0,14	0,368	0,357	0,346	0,336	0,326
0,15	0,365	0,355	0,345	0,335	0,326
0,16	0,362	0,353	0,343	0,334	0,326
0,17	0,360	0,351	0,342	0,334	0,326
0,18	0,358	0,349	0,341	0,333	0,326
0,19	0,356	0,348	0,341	0,333	0,326
0,20	0,355	0,347	0,340	0,333	0,326

Таблица 6

Отношение К / К _о

С	п
	0,850	0,875	0,900	0,925	0,950
0,10	1,253	1,205	1,159	1,114	1,072
0,11	1,235	1,191	1,148	1,107	1,068
0,12	1,220	1,179	1,140	1,102	1,065
0,13	1,207	1,169	1,132	1,097	1,063
0,14	1,195	1,160	1,126	1,093	1,061
0,15	1,186	1,153	1,120	1,089	1,059
0,16	1,177	1,146	1,116	1,087	1,059
0,17	1,170	1,140	1,112	1,085	1,058
0,18	1,163	1,136	1,109	1,083	1,058
0,19	1,158	1,132	1,107	1,082	1,058
0,20	1,153	1,129	1,105	1,082	1,059

Выполним расчет напряжений в маховике с помощью метода конечных элементов и сравним полученные результаты с результатами, приведенными выше.

Рассмотрим стальной маховик с Е =210 ГПа, р = 7 700 кг / м3 и о= 620 МПа. Внешний радиус маховика Ъ = 0,5 м, а величина ha = 0,05 м. Пусть с принимает зна чения 0,1 и 0,2, а параметр п равен 0,85. Тогда два варианта параметров маховика с гиперболическим профилем и массой, равной массе маховика с постоянной толщиной, будут иметь следующий вид:

с = 0,1, а = 0,05 м, Л_Ъ=0,042 5м, ^ = 0,088 5 м, п = 0,319(35) с = 0,2, а = 0,10 м, Л_Ъ =0,042 5 м, у 0,075 2 м, п = 0,354.

При расчете методом конечных элементов определялась максимальная угловая скорость щ , при которой эквивалентные напряжения на внутреннем радиусе достигают величины о ^ (рис. 5).

Как показывает анализ результатов, напряжения в маховиках равномерно распределены по толщине. Это позволяет сделать вывод о правомерности использования дисковой модели для расчета маховиков, параметры которых определяются равенствами (35).

Значения максимальной угловой скорости, при которой происходит разрушение маховика, представлены в табл. 7. Величина щ ⁽¹⁾ определена с помощью метода конечных элементов, а величина ® ⁽²⁾_шах - с помощью формулы (22).

Таблица 7

Максимальная скорость вращения

С	Щ <1)тах. рад / с)	Щ <2)тах. рад / с
0,1	716	729
0,2	678	686

Как видно из табл. 7, дисковая модель в рассматриваемых примерах дает результаты, хорошо совпадающие с результатами решения осесимметричной задачи теории упругости методом конечных элементов.

Отметим, что по мере уменьшения параметров с и п распределение напряжений по толщине маховика все более отличается от равномерного (рис. 6). А вблизи малого радиуса распределение напряжений уже явно не соответствует дисковой модели.

Таким образом, авторами с использованием дисковой модели решена задача определения параметров напряженного состояния маховика с гиперболическим профилем. Получены уравнения, позволяющие найти максимальную скорость вращения маховика, при которой начинается его разрушение. Определены массовая энергоемкость и коэффициент формы маховика. Найдены диапазоны изменения параметров маховика, при которых возможно использование дисковой модели. Выполнено сравнение аналитических решений с решениями, полученными методом конечных элементов.