Определение механических характеристик трансверсально-изотропного волоконного контура по изотропным свойствам компонентов

PNRPU MECHANICS BULLETIN

Волоконно-оптический гироскоп (ВОГ) – это современный оптический датчик вращения, который измеряет угловую скорость объекта, на котором он установлен [1, 2]. Принцип действия ВОГ основан на эффекте Саньяка [3, 4]. Сущность эффекта состоит в том, что разность фазовых набегов двух световых волн, распространяющихся по замкнутому контуру в противоположных направлениях при вращении контура вокруг оси, нормальной к его плоскости, пропорциональна угловой скорости вращения и площади контура, который обходят встречные волны. В волоконно-оптическом гироскопе свет распространяется в волоконном контуре (ВК), который состоит из квадрупольно намотанного оптического волокна, склеенного компаундом (рис. 1). В процессе эксплуатации ВК подвержен воздействию внешних механических факторов. Резонанс, возникающий при вибрационном воздействии, приводит к изменению напряженно-деформированного состояния в волоконном контуре. Напряжения, возникающие в кварцевом световоде оптического волокна, меняют его оптические постоянные, вследствие чего происходит искажение сигнала ВОГ: возникает «кажущаяся» угловая скорость [5]. Собственные частоты колебаний ВК, определяемые механическими характеристиками материалов, геометрией и граничными условиями, должны учитываться при проектировании ВОГ, чтобы исключить явление резонанса в рабочем диапазоне частот.

Волоконный контур является композиционным материалом, который состоит из четырех компонентов с упорядоченной гексагональной структурой: кварцевый оптический световод, первичное защитно-упрочняющее покрытие, вторичное защитно-упрочняющее покрытие, матрица из компаунда (рис. 2).

Рис. 1. Волоконный контур

Рис. 2. Поперечное сечение волоконного контура

Моделирование волоконного контура вариационно-разностными методами требует больших вычислительных мощностей, так как дискретизация сложной по строению расчетной области приводит к огромному количеству уравнений [6]. Для упрощения модели ВК осуществим переход от композита к трансверсально-изотропному однородному материалу, имеющему 5 независимых упругих констант, которые можно определить по изотропным механическим свойствам компонентов [7]. Применение такой модели определяющих соотношений является актуальной и широко используется для моделирования нестационарных тепловых процессов, протекающих в ВК [8, 9].

1. Постановка задачи

Чтобы осуществить переход от многокомпонентного ВК к однородному трансвер- сально-изотропному телу, рассмотрим элементарный объем (рис. 3), для которого необ- ходимо решить четыре задачи [10].

Напряженно-деформированное состояние элементарного объема в рамках гипотезы о малых деформациях описывается системой уравнений [11]:

уравнения равновесия aij, j = 0, i, j = 1,2,3,(1)

геометрические соотношения ej = 2(u, j + uj ,i), физические соотношения a j = 2^s ij +X5 a e kk.

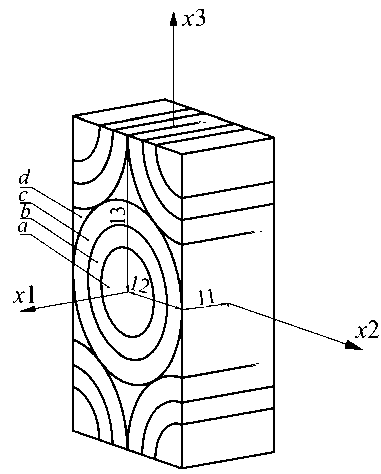
Рис. 3. Элементарный объем

Здесь G ij - тензор напряжений; £ j - тензор малых деформаций; Ui - вектор перемеще-

,       Ev              E                 „ тт„ _ п ний; р - плотность материала; К = ----—----- и р = —----- - коэффициенты Ламе; Е -(1 + v)(1 - 2v)        2(1 + v)

модуль упругости; v - коэффициент Пуассона; Ь_у - символ Кронекера.

Граничные условия для сопряжения слоев a - b , b - c , c - d :

и = uv, u,=u ; и — и,, ia ib; ib ic; ic id,

°ija • ni = °ijb • ni; °ijb • ni = °ijc • ni; °ijc • ni = °ijd • ni •

Граничные условия для задачи I (растяжение по оси x ₁ ):

• U1|X1 =11 = 211; U1|x =-11 = 0, ux,=± 1i = 0, i = 2,3, °jx,=±1i = 0, i * j•

Граничные условия для задачи II (растяжение по оси x ₂ ):

U2|x2 =12 = 212; U2|x2 =-12 = 0, Uixi =± 1i = 0, i = I,3, °jxi=± 1i = 0, i * j•

Граничные условия для задачи III (растяжение по оси x ₃ ):

• U3|x3 =13 = 213; U3|x3 =-13 = 0, uixi =± 1i = 0, i = 1,2, °jx,=± 1i = 0, i * j•

Граничные условия для задачи IV (сдвиг вдоль осей x ₁ и x ₂ ):

• U1|x2 = 12 = 12; U1|x2 =-12 = 0; °i2|x2 =± 12 = 0, i = 2,3, U2|x1 =11 = 11; U2|x1=-11 = 0; °i1|x2 =± 12 = 0, i = 1,3, U3x3 =±a3 = 0; °i3|x3 =±a3 = 0, i = 1,2.

Запишем физические соотношения для трансверсально-изотропного тела в матричном виде [12]:

				c C 1122	0
'° 11		^ 1111	c C 1122		0 0	0	0		8 11
° 22		c C 1122	c C 2222	c C 2233		0	0		8 22
° 33 1	r =	c C 1122	c C 2233	c C 2222		0	0	1	£ 33	> .	(9)
					Ь           X "2( C 2222 - C 2233 ) 0
° 23		0	0	0		0	0		8 23
° 13		0	0	0		C 1212	0		8 13
_° 12 .		0	0	0	0	0	c C 1212		£ 12

Из решения задачи (1)–(5) определяется коэффициент C ₁₁₁₁

C1111 = V j^ll (x1,x2,x3)dV.

Из решения задачи (1)–(4), (6) определяются коэффициенты C ₁₁₂₂ , C ₂₂₂₂ :

C1122 = v ри (xi, x 2, x з)dV;

C2222 = V j°22 (x1, x 2, x3 ) dV'

Из решения задачи (1)–(4), (7) определяется коэффициент C ₂₂₃₃ :

C2233 = V j°22 (x1, x 2, x3 ) dV.

Из решения задачи (1)–(4), (8) определяется коэффициент C ₁₂₁₂ :

C1212 = V j°12 (x1, x 2, x 3 ) dV.

Переход к техническим константам осуществляется с помощью соотношений

^E1 = C 1111

² 2 C ₁₁₂₂

C 2222 + C 2233

C 1122

C 2222 + C 2233

E ₂

C 1111 ⁽ C 2222

+ C 2233 )   ² C 1122 l⁽ C 2222 + C 2233

C ₁₁₁₁ C ₂₂₂₂

² C 1122

^V 23

C 1111 C 2233

² C 1122

C 1111 C 2222

² C 1122

12 = H212 -

Выражение для плотности

P = V ( p a ^V a ⁺ p b ^V b ⁺ p c ^V c ⁺ P d ^V d ) .

• 2.    Реализация вычислительных процедур

Для решения задач (1)–(8) использован метод конечных элементов (МКЭ), реализованный в программном комплексе Creo Simulate 2.0 [13].

На рис. 4 показана сеточная модель элементарного объема.

Для дискретизации элементарного объема был выбран 10-узловой тетраэдрический конечный элемент. В нем используется квадратичная аппроксимация функции формы, которая гарантирует непрерывность перемещений, и линейное изменение в объеме КЭ деформаций и напряжений. Размер конечного элемента принимался из условия, что при двукратном сгущении сетки интегральные суммы искомых компонент тензора напряжений по объему элементарной ячейки изменялись менее чем на 1 %.

Рис. 4. Сеточная модель

На рис. 5 приведены распределения напряжений в элементарном объеме, которые требуются для отыскания констант (10)–(14).

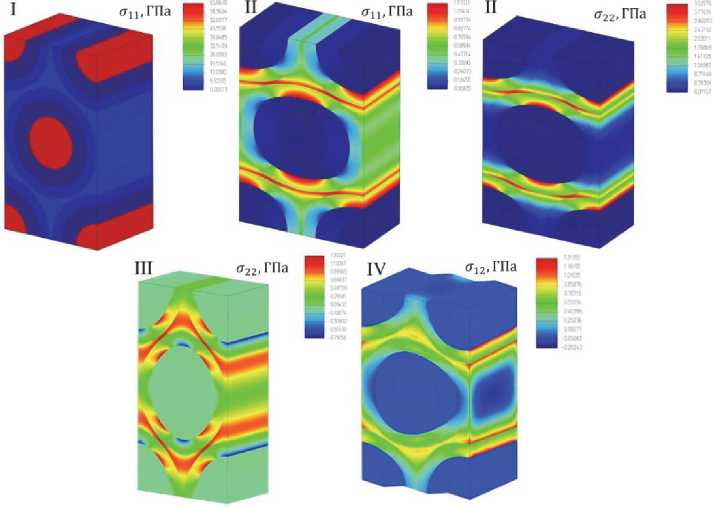
Рис. 5. Распределения напряжений

Задачи (1)–(8) решались для значений упругих характеристик в широком диапазоне температур. На рис. 6 показаны механические характеристики трансверсально-изотропного ВК при различных температурах.

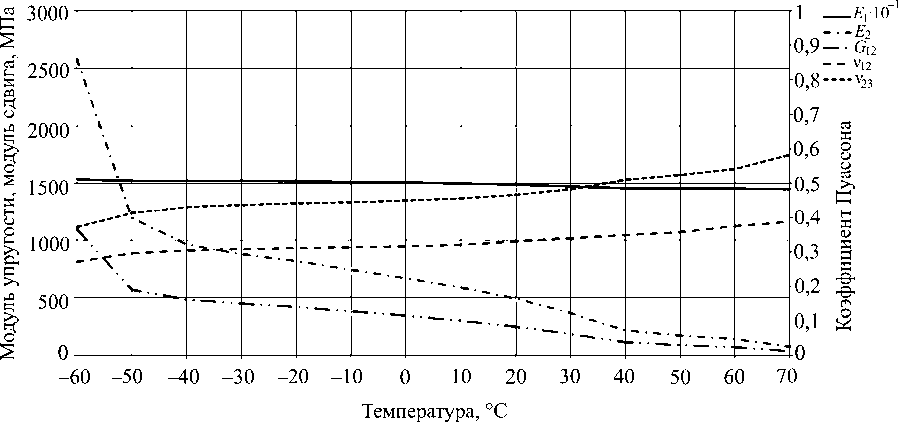
Рис. 6. Механические характеристики

Из рис. 6 видно, что коэффициент Пуассона V23 достигает значения V23 = 0,6 при t = 70 °C. Как известно, для большинства материалов коэффициент Пуассона лежит в диапазоне 0 < V < 0,5 , однако по современным представлениям диапазон возможных значений ν существенно расширен за оба предела [14]. Высокие значения коэффициента Пуассона оказываются характерны для некоторых анизотропных кристаллов и композиционных материалов [15–17].

• 3.    Экспериментальная проверка

Для верификации найденных характеристик был использован динамический подход, который предполагает сравнение собственных частот и форм колебаний модели и реального объекта [18]. Для серии экспериментов брались два волоконных контура, по каждому из которых производилось по десять ударов резиновым молотком. После удара в ВК возникают колебания, которые фиксировались портативным регистратором-анализатором динамических параметров MIC-200M. С целью обеспечения близкой к нулю жесткости крепления ВК подвешивался на нити. На ВК клеился трехосевой пьезоакселерометр массой 0,02 кг. На рис. 7 представлены характерные показания датчика по каналам, соответствующим осевому и радиальному направлениям.

Применив к сигналам алгоритм быстрого преобразования Фурье, получим спектр частот (рис. 8).

Из рис. 8 видно, что в диапазоне 0–1000 Гц ВК имеет 4 резонансных пика (2 в осевом и 2 в радиальном направлениях).

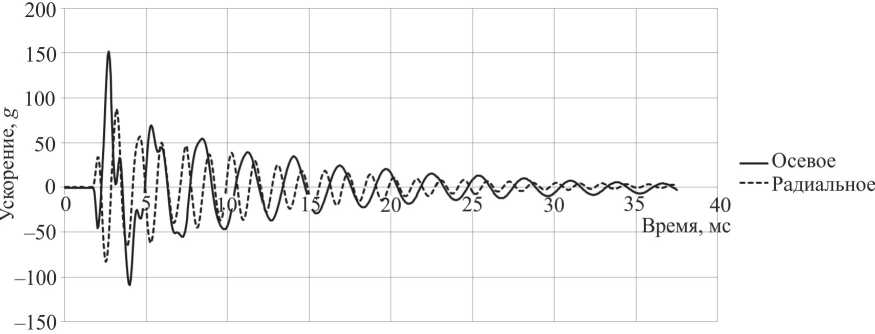
Рис. 7. Показания датчика

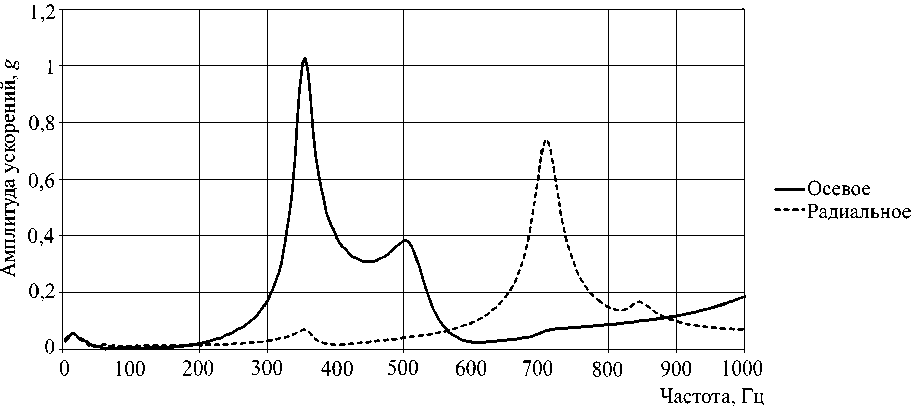
Рис. 8. Спектр частот

• 4.    Сравнение полученных данных

Для сравнения полученных данных был проведен модальный анализ ВК методом конечных элементов в программном комплексе Creo Simulate 2.0.

Для задания ориентации констант трансверсально-изотропного материала волоконного контура вводилась цилиндрическая система координат. Использовались константы, определенные для температуры 20 °С. В модели ВК учитывалась масса датчика (рис. 9).

Как и при решении задач (1)–(8), в качестве конечного элемента выбран 10-узловой тетраэдр. Размер конечного элемента принимался из условия, что при двукратном измельчении сетки отличие по собственным частотам текущего и предшествующего решений менее 1 %.

На рис. 10 представлены первые четыре формы колебаний волоконного контура с присоединенной массой. Из расчета исключены близкие к нулю собственные частоты, соответствующие перемещениям ВК как абсолютно жесткого тела. Модальный анализ показал, что первая и вторая формы имеют максимальные перемещения в осевом направлении, а третья и четвертая – в радиальном.

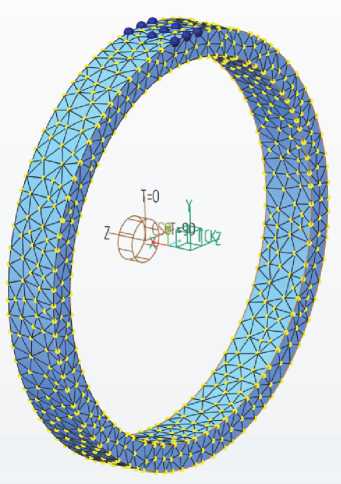
Рис. 9. Модель ВК с присоединенной массой

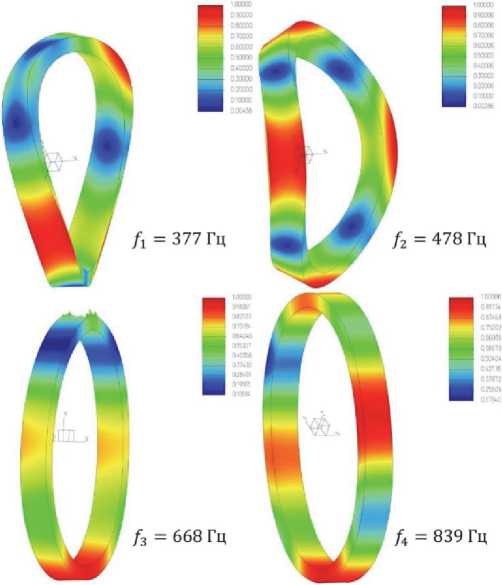
Рис. 10. Формы колебаний ВК

В сводной таблице представлены средние значения экспериментальных данных колебаний ВК с датчиком и модального анализа.

Сравнение результатов расчета и эксперимента

Параметры	форма 1	форма 2	форма 3	форма 4
Экспериментальная частота, Гц	355	505	705	830
Частота из модального анализа, Гц	377	478	668	839
Относительная погрешность, %	6,2	5,3	5,2	1,1

Выводы

• 1.    Методом конечных элементов решены задачи для нахождения механических констант трансверсально-изотропного материала волоконного контура.

• 2.    С помощью эксперимента были установлены собственные частоты колебаний волоконного контура с приклеенным датчиком.

• 3.    Сравнение экспериментальных данных с результатами модального анализа показало удовлетворительное совпадение.

• 4.    Для преодоления сложностей, связанных с затратами большого количества времени и машинных ресурсов, при моделировании колебательных процессов волоконнооптического гироскопа можно перейти от многокомпонентного композита к однородному трансверсально-изотропному материалу волоконного контура.

• 5.    Полученные коэффициенты для трансверсально-изотропного тела могут быть использованы в определяющих соотношениях модели однородного материала волоконного контура.