Определение механических характеристик зерна ячменя при статическом силовом нагружении

Современный технологический процесс производства зерна, как и многих сельхозкультур, невозможен без использования машин. Однако при механизированной обработке партий зерна в результате взаимодействия с рабочими органами машин отдельные зерна получают травмы, т.е. механически повреждаются. Количество механически поврежденных зерен в партии (далее – механических повреждений), по данным [1; 2], достигает 60% и более, значительно превышая пределы стандартов на качество зернового материала, соответственно это влияет на его дальнейшее использование. Для семенного зерна в таком случает отмечают снижение полевой всхожести и урожайности, для продовольственного – ухудшение технологических свойств. Кроме того, партии зерна с механическими повреждениями менее стойки в хранении. Так как полностью исключить повреждения зерна при механизированной обработке невозможно, по-

иск путей снижения механических повреждений за счет совершенствования технологической схемы обработки и технических средств ее реализации актуален, имеет важное народно-хозяйственное значение.

Постановка задачи

Рассмотрим в качестве объекта исследования технологический процесс механизированной обработки такой важной сельхозкультуры, как ячмень. Его зерна механически повреждаются при контактном взаимодействии с рабочими органами сельхозмашин. Происходит это по причине нарушения условия прочности [3; 4].

d   kd СУ_{st     b} ,                                               (1)

где СУ и СУ – соответственно эквивалентные статические и динамические напряжения, возникающие в зерне, Па; СУ – предел прочности зерна на сжатие, Па; k – коэффициент динамики, зависящий от скорости соударения зерна с рабочим органом и величины статической деформации.

Представление о динамическом силовом нагружении зерновки ячменя может быть получено на основании его статического взаимодействия с рабочими органами сельхозмашин. Передача давлений в местах соприкосновения взаимодействующих тел происходит по малым площадкам. Тело около такой площадки контакта испытывает объемное напряженное состояние (рис. 1). Напряжения и деформации при контакте тел разной формы определяются методами теории упругости [4; 5] .

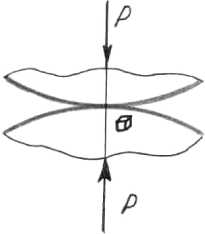
Рис. 1 . Напряжения, возникающие в результате контакта двух тел, ограниченных криволинейными поверхностями

Оценка величины возникающих в зерне механических напряжений может быть получена при известном значении нагрузки и знании формы зерновки. Для оценки контактных напряжений, возникающих в зерне пшеницы, гороха, сои, гречихи, кукурузы, предлагались различные математические зависимости [2; 9]. Однако при одинаковом силовом взаимодействии с рабочими органами машин напряжения в зерновках этих культур должны заведомо отличаться от напряжений, возникающих в зерне ячменя, потому что у нее отличная от них форма зерновки, предлагаемые зависимости не приемлемы для такого случая.

Задача исследований – моделирование формы ячменя и установление зависимости возникающих в нем напряжений от геометрических и механических параметров зерна.

Теория

Для определения напряжений в зерновке ячменя нами предложена ее геометрическая форма в виде тороида (рис. 2). Такая фигура образуется в результате эксцентричного вращения дуги BCD окружности с центром в точке O и радиусом R вокруг оси AZ (образующая окружность), совпадающей с плоскостью окружности, величина эксцентриситета при этом равна AO = r (направляющая окружность).

Определим геометрические параметры образовавшейся фигуры. Рассмотрим произвольную точку M(x0, 0, z0) окружности x r2+z2R2.(2)

При вращении вокруг оси АZ в плоскости XOY она будет описывать окружность x2 + y2   x02;z   z0.(3)

Поскольку x0r 2 z02R2,(4)

раскрывая скобки и приведя подобные, получаем

2 x0 r  x0 + r2 + z02  R2.(5)

С учетом (2)

2 x2 + y2 r  x2 + r2 + y2 + z2 R2 .(6)

Возведя обе части уравнения в квадрат, получим уравнение тора в Декартовой системе координат

4x2 y2  r2   x2 r2 y2  z2 R2 2   0.(7)

По этому уравнению можно определить длину зерновки I .

При                          x 0; y 0; z =±vR2r2

l 2z 2VR2r2

Такое же выражение может быть получено из прямоу гольного треугольника AOB l 2 AB 2 BO ² AO ²   2V R ² r ²

В то же время диаметр зерновки d d = 2AC = 2(OC – OA) = 2(R – r).

Решая совместно уравнения (9) и (11), получим значения Rиr l2d2

R            , r.

4d4

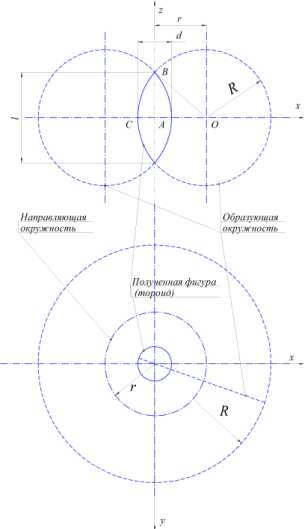
Рис. 2. Зерновка ячменя в виде тороида (расчетная схема)

Полученная фигура тороида применительно к зерну ячменя сорта Омский 95 в трех проекциях и аксонометрии представлена на рис. 3.

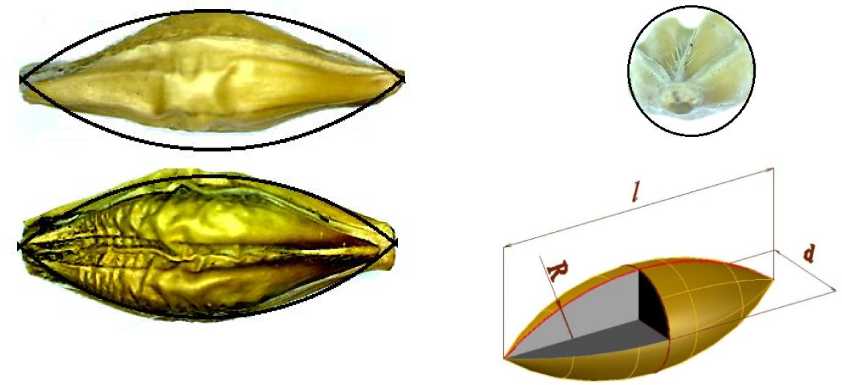
Рис. 3 . Зерно ячменя, аппроксимированное тороидом

Определим объем полученной фигуры как тела, вращающегося вокруг оси z (рис. 5).

Согласно [6] объем тела вращения вычисляем по выражению b

V= J S x dz , a где Sx – площадь сечения полученного тела вращения плоскостью, проходящей через точку M, перпендикулярной оси z

Sx = 71 x ² .

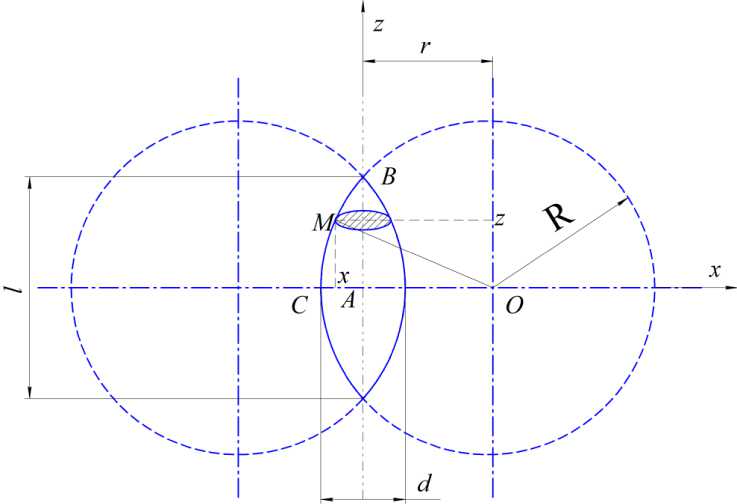
Рис. 4 . Определение объема тороида (расчетная схема)

ll

V 2       R ² z ² r ² dz 2 R ² z ²  2 r R ² z ² r ² dz

R ² l  ^l 2 r

l

l ²

R ²        R ² arcsin

l

2 R

r ² l

Учитывая, что

R2     = r, получим

V   R ²

_l l ³ 12 R ²

2 r arcsin

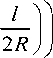
Считая, что рабочие органы сельхозмашин, несмотря на большое разнообразие их форм в местах контакта, в общем случае можно свести к плоскости или цилиндру, рассмотрим представленные на рис. 5 наиболее вероятные варианты статических контактов предлагаемой модели зерновки с предполагаемыми формами рабочих органов сельхозмашин под воздействием сжимающих сил P . Повреждение зерна в процессе механизированной обработки и транспортировки зерновых партий возможно при падении зерна с большой высоты, например, при разгрузке транспортного средства на бетонный пол завальной ямы поточной линии (рис. 5, а ) или при контакте с цилиндрическими кромками рабочих органов машин (рис. 5, б , в ).

В результате взаимодействия тел в месте контакта образуется эллиптическая площадка с полуосями c и t . Зная их значения по формуле (15), рассчитывается значение наибольшего сжимающего напряжения

3 P

"max " 2;тct ’ где Р - значение сжимающей силы, Н.

Наиболее опасная точка расположена на линии действия силы на некоторой глубине от площадки взаимодействия, зависящей от соотношения полуосей эллипса кон- такта с/t .

Значения c и t могут быть определены по методике для обобщенного случая контакта двух соприкасающихся тел [5; 6]: сначала вычисляем главные радиусы кривизны А, Р'\ , А, А 2 и угол ф между главными плоскостями кривизны:

для контакта тороида:

• -    с плоскостью го (рис. 5, а ); р_х = d) 2; р= = R ; а = °⁰; Р 2 = °⁰; ф = 90°;

• -    с цилиндром при параллельном расположении главной оси тороида и оси цилиндрической кромки (рис. 5, б ); _Pv= d /2; р= = R ; А = R i; р= = °⁰; ф = 90°;

• -    с цилиндром при скрещивании главной оси тороида с осью цилиндрической кромки (рис. 5, в ); р_х = d/ 2 ; р\ = R ; а= °⁰; Р = = R i; ф = 90°.

Далее определяем значение вспомогательного угла ф по формуле

11  111111

2cos 2

f/z-arccos^1       ^2        VA А Л А Р2 )     .(16)

arccos

— + ” + — + 7

Таким образом, для контакта тороида:

• -    с плоскостью (о (рис. 5, а ):

2Rd2 у/ = arccos

2R2dRd

– с цилиндром при параллельном расположении главной оси тороида и оси цилиндрической кромки (рис. 5, б ):

2 RR  dR dR ²

^ = arccos        1     1

RdR (2 RR + dR + dR )

– с цилиндром при скрещивании главной оси тороида с осью цилиндрической кромки (рис. 5, в ):

.

2 RR  dR dR ²

^ = arccos       1     1

RdR (2 RR + dR + dR )

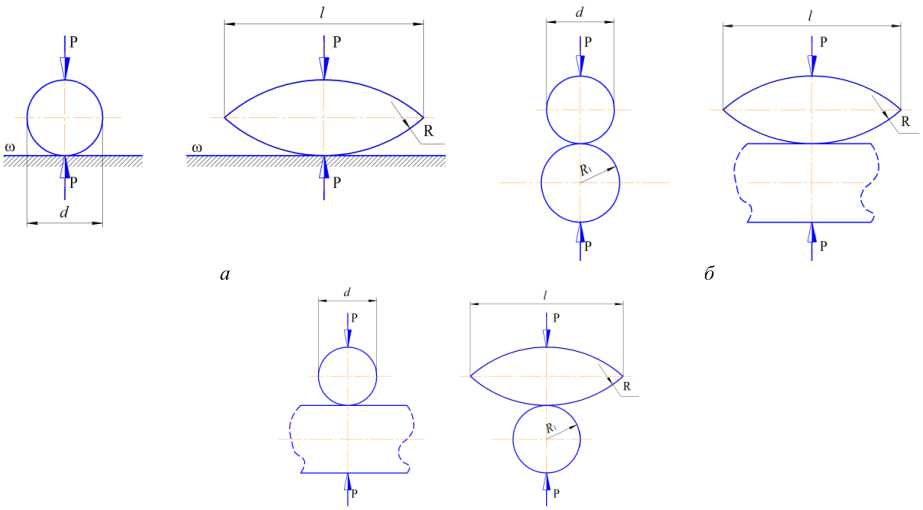
Рис. 5 . Варианты контакта зерна ячменя с рабочими органами машин: а – контакт с плоским рабочим органом ш ; б – контакт с цилиндрическим рабочим органом при скрещивании главной оси тороида с осью цилиндрической кромки; в – контакт с цилиндрическим рабочим органом при параллельном расположении главной оси тороида и оси цилиндрической кромки

Далее, зная значения вспомогательного угла у/ , по соответствующим таблицам [3; 4] путем интерполяции находят значения коэффициентов m и n , которые необходимы для определения полуосей эллипса касания по формулам.

сm

tn

³ тг\              P              1 1² 1 2²

3     4    1    1     1     1       E 1 E 2

1          р 1    р 1     2    р 2

3 71              P             1 1² 1 2²

3 4 1111   E 1¹ E 2²

V         ^1    Р 1    р 2    р 2

где М^--! и /^2 – коэффициенты Пуассона контактируемых тел; для ориентировочной оценки можно принять ^1 = ^2 = 0,3; Ei и ^*2 – модули упругости контактируемых тел, по [3; 4] для стали е₂ = 2,1∙10⁵ МПа.

Так как модуль упругости для зерна значительно меньше, чем для стали Е^ « Е₂ , значением ¹   2² можно пренебречь и выражения (20) и (21) примут вид

E 2

3 71            P 1 - р 2 _.

3     4    1     1     1     1

'        Р1   Р1   Р2

3 71            P 1 - р ² .

3     4    1     1     1     1

'        Р1 Р1   Р2

Однако в данных выражениях подлежит экспериментальному определению значение модуля упругости £*і для зерна.

Результаты экспериментов

Значение условного диаметра d вычисляют как среднее размеров ширины b и толщины c . По формулам (12), используя значение длины l и условного диаметра d , подсчитывают значения радиусов R и r .

Для установления габаритных размеров были взяты зерна ячменя трех сортов. Результаты измерения габаритных размеров зерна и значения параметров, рассчитанных по вышеприведенным геометрическим зависимостям (условный диаметр зерновки d , радиус образующей окружности R , радиус вращения направляющей окружности (эксцентриситет) r , объем зерновки V ) сведены в табл. 1.

Таблица 1

Параметры зерна ячменя

Сорт	Масса 1000 зерен, г	Размеры, мм			Расчетные параметры тороида
		оЗ У У у у:	оЗ У У р< У а	сЗ У У В у о н	сЗ S ^ У S у у S	5S ю о О щ Рч	У о $ н * „ э 2 ^^ & § н S m о н о оз о s о	§^ у &>в CO uQ О £	(D Д со щ О со У	У У 0) У о У н О
Омский 95	42,4 ± 0,73	9,26 ± \ 0,46	3,57 ± 0,12	2,76 ± 0,11	3,17	7,56	5,98	40,2	44,3 ± 2,6	10,20
Саша	52,7 ± 0,81	9,99 ± \ 0,51	4,23 ± 0,22	3,24 ± 0,16	3,73	7,62	5,75	60,7	51,6 ± 3,4	14,99
Ача	50,5 ± 0,75	9,65 ± \ 0,60	4,17 ± 0,18	3,26 ± 0,17	3,72	7,12	5,33	58,1	50,5 ± 2,9	13,08

Проверка адекватности предложенной модели зерновки в виде тороида проведена измерением объема реальной зерновки при кратковременном погружении пятисот зерен в мерный цилиндр с водой. Разница уровней жидкости до и после погружения зерна, разделенная на количество погруженных зерен, является средним фактическим значением объема зерна. Измерение объема зерновки проведено в пятикратной повторности. Согласно табл. 1 отклонение фактического объема зерновки от расчетного в зависимости от сорта – примерно 10–15%.

При определении Е_т зерновки ячменя за основу была взята методика [8; 9; 10]: сжатие предварительно подготовленных зерен разной влажности между наконечником индикатора и головкой винта микрометра специальной установки. Схема нагружения представлена на рис. 5, а . При помощи регулируемого источника тока нагружение и разгрузка проводились при постоянной скорости 4 Н/с до значения силы P .

В результате контактного статического взаимодействия с использованием измерительной лупы определялись значения полуосей эллипса c и t площадки контакта по отпечатку на предварительно вставленной между зерном и наконечником окрашенной бумаги (при значении силы P перед самым моментом его разрушения). Экспериментальные значения указанных размеров c и t от влажности W ячменя сорта Омский 95 при силовом нагружении представлены в табл. 2.

Таблица 2

Параметры сжатия зерна ячменя

0,00

20,00

15,00

10,00

5,00

25         35

W %

а

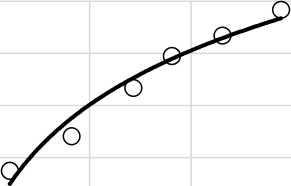
б

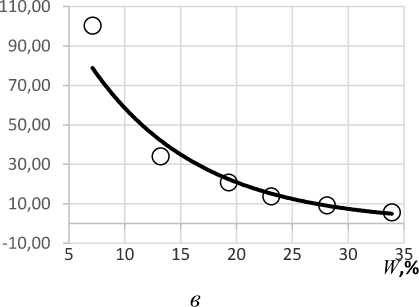
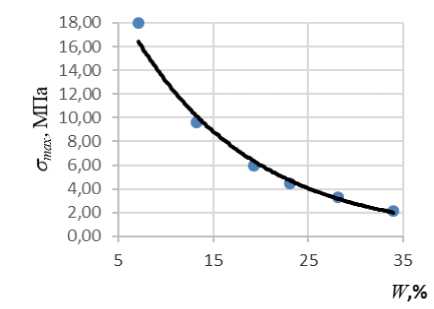
Рис. 6. Механические характеристики зерна в зависимости от влажности W: а – площадь контакта S_пк = f(W) ; б – предельно сжимающее напряжение G_max = f(W) ; в – модуль упругости Е = f(W)

Влажность W , %	Значение силы, сжимающей зерно P , Н	Размер полуосей эллипса контакта, мм		Площадь эллипса контакта Sпк    ct , мм2	Наибольшее напряжение в центре площадки контакта , МПа	Модуль упругости Е 1 , МПа
		c	t
7,1	44,853	1,37	0,87	3,74	17,97	100,40
13,2	45,3605	1,78	1,14	6,37	10,67	46,30
19,3	46,43	2,34	1,59	11,69	5,96	20,86
23,1	44,238	2,64	1,78	14,76	4,49	13,84
28,1	36,5665	2,83	1,88	16,71	3,28	9,29
33,9	27,0625	3,01	2,03	19,20	2,11	5,71

Подсчитанное значение вспомогательного угла у/ для случая на рис. 5, а составило ^ « 71°, значения m и n по [3; 4] m = 1,27, n = 0,81. Значение суммарной кривизны

1 1 1 1 2 Rd     ₁₁

K =-- 1---1---1--=------= 0,763 мм = 763 мм •

1     1     2     2       ^Rd

Значения модуля упругости в зависимости от влажности будут получены после подстановки соответствующих параметров в (22) и (23)

E 1      1 1 ²

P 3 m ³ ₂

K 4 c      ¹¹

P 3 n ³

K 4 t

Полученные по выражению [24] значения модуля упругости зерна , а также значения площади контакта S_K = net и наибольшего напряжения а_тах, подсчитанного по формуле (15), показаны в табл. 2.

На рис. 6 представлены графические зависимости S_№ = f (W ), _CTmax = f(W ) ,

Ei= f (W ) •

Применяя метод наименьших квадратов, полученные экспериментальные кривые при 7 <  W < 35% аппроксимируются зависимостями

S = 10,166 In W -17,455 пк

<7 max = 28,638 c"    W                                   (25)

E   163,71 e ^{0,103 W}

Обсуждение результатов

Предложенная модель зерновки ячменя в виде тороида соответствует по объему реальной примерно на 85-90%.

Отмечается, что с увеличением влажности значение площади эллипса контакта при сжатии зерна увеличивается по логарифмическому закону, а значения наибольшего сжимающего напряжения и модуля упругости уменьшаются по экспоненциальному закону. У коэффициента достоверности аппроксимации достаточно высокое значение: П ² > 0,95.

Величина напряжений, возникающих в зерновках ячменя при механизированной обработке, зависит от кривизны контактируемых тел, модулей их упругости, коэффициентов Пуассона, влажности зернового материала, а также скорости соударения зерна с рабочим органом.

Выводы и заключение

Для снижения механических повреждений ячменя при механизированной обработке необходимо:

• -    проводить обработку при влажности зерна от 15 до 20% (зона упругих деформаций);

• -    следить за состоянием кромок рабочих органов, не допускать их заострения;

• -    применять рабочие органы из материала с модулем упругости значительно меньшим, чем у стали;

• -    снижать скорость соударения зерен с рабочим органом.

Использование полученных теоретических зависимостей позволит конструкторам сельхозмашин при известном значении сжимающей силы проводить оценку величины возникающих в ней напряжений.

• V.V. Trotsenko¹, A.I. Zabudsky¹, I.V. Trotsenko¹, N.V. Komendantova^{2 1}Omsk State Agrarian University named after P.A. Stolypin, Omsk ²Department of the Pension Fund of the Russian Federation in Omsk Region, Omsk

Determination of mechanical characteristics of barley grain under static force load