Определение минимального объема выборки



ОПРЕДЕЛЕНИЕ МИНИМАЛЬНОГО ОБЪЕМА ВЫБОРКИ

О- А. Бакаева

В данной статье приведены способы нахождения оптимального объема выборки л для нормального закона распределения, распределения Стьюдента, а также биномиального закона в зависимости от известных параметров этих законов распределения.

В науке часто, чтобы определить какую-либо величину, приходится проделывать ряд испытаний. Но бывает так, что и в этом случае истинное значение показателя абсолютно точно измерить не удается, оно получается с определенной долей погрешности. Исходя из формул доверительного интервала для нормального, биномиального распределения и распределения Стьюдента находится минимальное количество экспериментов, необходимое для получения достоверной информации.

В современных условиях цена эксперимента бывает достаточно высокой как в переносном, так и в прямом смысле. Это может быть связано и с использованием дорогостоящего оборудования, и с оплатой труда специалиста, и непосредственно с затратами ла сам опытный процесс. Поэтому задача определения минимального количества экспериментов для получения всей необходимой информации в целях ее последующей обработки является очень актуальной. На языке статистики эта задача сводится к определению минимального объема выборки.

Основная часть классической статистической теории предполагает нормальность распределения изучаемой случайной величины. Но на практике в большинстве случаев приходится сталкиваться с распределением, закон которого близок к одному из известных распределений, но далек от нормального. К наиболее употребительным распределениям можно отнести: непосредственно нормальное распределение и распределение Стьюдента, которые являются непрерывными, а также дискретное - биномиальное распределение. В зависимости от закона распределения и вычисляют необходимый объем выборки - п.

Нормальное распределение. Обычно в статистике решается задача определения доверительных интервалов, покрывающих параметр о, с надежностью у и точностью 5, где а - математическое ожидание нормально го распределения.

Пусть параметры распределения таковы;

М(Х) = а, сг(Х) = —=, Потребуем, чтобы V»

выполнялось соотношение Р(|Х —а| < 6) = у, где у - заданная надежность, получим Р(|Х — а| < 6) — 2Ф^У заменив X на X и ст на ст(Х) = —. Тогда

Р(|Х-а| <  5) ^2ф(^^ = 2Ф(<),  (1)

где

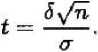
г,                                        с to

Найдя из последнего равенства о = —= имеем право написать

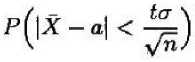
= 2Ф(<).

Приняв во внимание, что вероятность Р задана и равна у, окончательно имеем (чтобы получить рабочую формулу, выборочную среднюю обозначим за х)

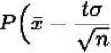
< а < х р 7^) ™ 2Ф(1) = у.

Смысл полученного отношения таков: с надежностью у можно утверждать, что до-„            /_ to _ to \ верительный интервал х--т=,х Ч—= по-

V vn Vn/ крывает неизвестный параметр а; точность оценки 6 = to/Vn Число t определяется

из равенства 2Ф(1) — 7, или Ф(1) = 7/2; по таблице функции Лапласа находят аргумент t, которому соответствует значение функции Лапласа, равное 7/2 [1].

Если известно математическое ожидание с наперед заданной точностью 8 и надежностью 7, то минимальный объем выборки, который обеспечит эту точность, находят по формуле

- ter как следствие равенства й = —=.

Учитывая, что характеристиками стан дартного нормального распределения являются а = 0 и tr = 1, то формула (1) примет вид:

Р(|Х[ < 5) = 2Ф(8^ = 2^(t),(4)

где t = 5Vn.(5)

Из последнего равенства следует, что минимальный объем выборки будет равен:

t2

п = T9-(**)

Также можно использовать аппроксимацию t « 4, 91 [а^0,14 — (1 — а)⁰’¹⁴]- Тогда получается [2]

п = 24,1081 ( у р14 - (1 - а)0-14] Г Id                       J J

Как показывает полученная формула, минимальное число опытов прямо пропорционально квадрату значения t, которое находится по табличным значениям функции Лапласа, Ф(() = 7/2, где 7 - это надежность. То есть с увеличением надежности минимальное число элементов увеличивается' в параболической зависимости. С другой стороны, минимальное число опытов обратно пропорционально точности, с которой измеряется среднее значение признака. С увеличением 5, т. е. с уменьшением точности, число элементов уменьшается, а с уменьшением 3, т. е. с увеличением точности, число элементов, наоборот, увеличивается.

О применимости формул (*) и (**) относительно общего количества экспериментов речь пойдет ниже.

Известно, что при неограниченном возрастании объема выборки п распределение Стьюдента стремится к нормальному. Поэтому практически при п > 30 можно вместо распределения Стьюдента пользоваться нормальным распределением. Однако важно, что для малых объемов выборок (п < 30), в особенности для малых значений п, замена распределения нормальным приводит к грубым ошибкам, а именно к неоправданному сужению доверительного интервала, т. е. к повышению точности оценки. Например, если п — 5 и 7 = 0,99, то пользуясь распределением Стьюдента, имеем Ц = 4,6, а используя функцию Лапласа, найдем Ц = 2,58, т. е, доверительный интервал в последнем случае окажется более узким, чем найденный по распределению Стьюдента. То обстоятельство, что распределение Стьюдента при малой выборке дает широкий доверительный интервал вовсе не свидетельствует о непригодности метода Стьюдента, а объясняется тем, что малая выборка содержит малую информацию об интересующем нас признаке.

Распределение Стьюдента определяется параметром п - объемом выборки (или числом степеней свободы к — п — 1) и не зависит от неизвестных параметров а и а; эта особенность является его большим достоинством.

При достаточно больших значениях п объема выборки выборочная и исправленная дисперсии различаются мало. На практике пользуются исправленной дисперсией, если примерно п < 30 (напомним, что именно при небольших размерах выборок и используется распределение Стьюдента, тогда как при п > 30 практически любая случайная величина аппроксимируется нормальным распределением).

При неизвестной дисперсии необходимый объем выборки определяется из соотношения

- е ias где ta - а-квантиль распределения Стьюдента при f — п степенях свободы; s и ж - выборочные оценки соответственно стандартного отклонения и среднего значения [2].

Необходимые значения ^^ рассчитаны и могут быть найдены по таблицам [2, табл. 49].

Определение объема выборки происходит в следующей последовательности. Сначала по заданным величинам о — - и а и предпо-латаемому значению коэффициента вариация

S , ta(n)

v — - находят по таблице значение —и х Vn по нему определяют искомое значение п. Ес- ли для найденного объема выборки п выборочное значение окажется больше предполагавшегося, то эксперимент должен быть продолжен.

Замечание. Если а = 0,975, то, как частный случай, из выражения

<0,975 (п) = 2^               (7)

следует, что объем выборки

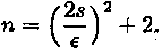
В этом случае по заданной абсолютной ошибке е и предполагаемому стандартному отклонению s может быть непосредственно определен объем необходимой выборки п.

Биномиальное распределение. Пусть производятся независимые испытания с неизвестной вероятностью р появления события А в каждом испытании. Ставится задача найти доверительный интервал для оценки вероятности, в случае биномиального распределения это можно будет сделать с помощью относительной частоты р = — . Учитывая, что п

Р(|Х-а|<5) = 2ф(£),     (9)

и заменив случайную величину X и ее математическое ожидание а соответственно случайной величиной IV и ее математическим ожиданием р, получим приближенное (так как относительная частота распределена приближенно нормально) равенство

F(iIV-p| <6} = 2ф(-А = 7.   (10)

\ СТ /

Как известно, для биномиального распределения дисперсия находится по формуле P(W) = —, а среднее квадратическое откло-п нение как квадратный корень из дисперсии ст = VD(W) = ^J^’ где 9 ~ 1 — р - вероятность не появления события А, тогда подставив данные выражения в формулу (10), получают:

P(|W-p| < 5) = ^2Ф(^) = ²^(^f) = 7, (И)

где

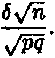
Следовательно,

^-"К^)

= 2Ф^ — 7-

Можно выразить точность 6 = t^/^, откуда минимальный объем выборки, если вероятность р появления события известна, находится по формуле:

П~ 5=

(* * *)

где t - значение функции Лапласа. Если вероятность появления события явно не задаг-на, то находим ее из соотношения р — , где m - число появления события, ап- число испытаний. Тогда минимальный объем выборки будет

.2 тг = t

/ m m2 х

XnJ2 n2^2/

(* * **)

Если n достаточно велико и вероятность р не очень близка к пулю и к единице, то можно считать, что относительная частота распределена приближенно нормально.

Также можно аппроксимировать практически любое распределение нормальным при достаточном объеме выборки. Об этом свидетельствует и Центральная предельная теорема А. М. Ляпунова. Отсюда следует, что практически все статистические распределения должны приближаться к нормальному распределению как к идеальной предельной форме, если только можно располагать достаточно большим числом наблюдений. То есть, если объем выборки > 30 и случайная величина близки к нормальному распределению, то минимальный размер выборки опре-,2 2 t ст .           , деляется соотношением п — ——-. А если объ-ем выборки < 30 и дисперсия неизвестна, то исходя из распределения Стьюдента и таб-<

личных значений ——, так как при новых Vn условиях формула (*} не гарантирует того, что полученное число экспериментов будет достаточным.