Определение нагрузки с учетом ледового воротника в гидротехническом строительстве

Задача о влиянии ледовых воротников на нагрузки трудно поддается аналитическому решению, поэтому целесообразно применение численного моделирования. Классический набор моделей в программных комплексах сильно ограничен, обычно используется статическая постановка и ближайшая стандартная модель льда [1]. Предлагаемая модель основана на методе дискретных элементов. Преимущество данной модели состоит в возможности описания процесса разрушения льда [2-5]. При использовании метода конечных элементов (КЭ) и конечных разностей (КР) имеется существенная проблема, заключающаяся в том, что разрушенный материал не участвует в дальнейшем взаимодействии, что не является точным подходом. Если для получения результатов достаточно статической постановки и только одного макси

мального значения нагрузки, то возможно применение методов КЭ и КР, однако, для описания всего процесса разрушения метод дискретных элементов (ДЭ) будет иметь преимущество [6-9].

По методу ДЭ в плоском случае ледовая область моделируется дисками разных диаметров. Эта модель широко используется при моделировании поведения гео-материалов при сжатии. Все параметры среды (прочность при сжатии, сдвиге, отрыве) определяются определенными константами, найденными из сопоставления модельного образца льда с натурным. Сдвиговая прочность определяется законом Кулона-Мора . На рис. 1 представлен пример с дисками

Рис. 1. Лёд, моделируемый дисками разного диаметра разного диаметра. Преимущество этого метода по сравнению с другими методами состоит в возможности рассмотрения последовательного разрушения среды.

До начала моделирования происходит заполнение заданной области дисками, и их упаковка до достижения заданной плотности льда. Ледовые характеристики принимались как на основании известных физических экспериментов, так и на основании статей и справочных данных [10-20]. Для расчетов был использован случайный фактор формирования заполнения, вследствие чего результат является стохастическим. Смежные элементы, в пределах заданного предела, образуют единый материал. Для получения достоверных оценок производилось несколько экспериментов при одних входных параметрах. Количество повторных моделирований определяется требуемой относительной ошибкой результата. Обычно, пять запусков позволяет получить результат с относительной ошибкой, не превышающей нескольких процентов.

В процессе моделирования происходит смещение образованной ледовой структуры в сторону сооружения. Фиксируется ледовая нагрузка в разные моменты времени. Материал считается разрушенным при расхождении элементов (дисков) на расстояние больше заданного, то есть, когда физический контакт нарушается, и элементы перестают взаимодействовать. Отколовшийся элемент может взаимодействовать с другими только оказывая сжимающее или сдвигающее напряжение.

ПОСТАНОВКА ЗАДАЧИ

В двумерном случае рассматривается вертикальная неподвижная стенка, к которой примыкает ровный лёд с образовавшимся ледовым воротником. Для ровного льда задается начальная толщина, соответствующая определенному количеству морозоградусодней (МГД). Размеры ледового воротника принимались в соответствии с результатами термодинамического моделирования [21-24]. На рис. 2 приведен пример возможной формы ледового воротника для целей моделирования методом ДЭ.

Лёд движется в направлении неподвижной стенки и разрушается. Ледовая нагрузка меняется во времени вследствие образования трещин и разрушения льда. Часто происходит откол фрагмента, как показано на рис. 3. Для дальнейшего рассмотрения представляет интерес максимальная нагрузка, соответствующая разрушению ледового воротника, полученная в опыте.

Фиксируются значения нагрузки от времени, и отбирается релевантный максимум, то есть тот, когда происходит разрушение ледового воротника. На рис. 4 представлен пример графика зависимости ледовой нагрузки от времени для случая ледового воротника толщиной 1.5 м от поверхности и шириной 1.5 м от поверхности сооружения (лёд толщиной 1 м).

Для оценки изменения нагрузки на вмерзшую в лед цилиндрическую опору, при наличии ледовых воротников, рассмотрена следующая задача (рис. 5). Опора расположена в ледовом

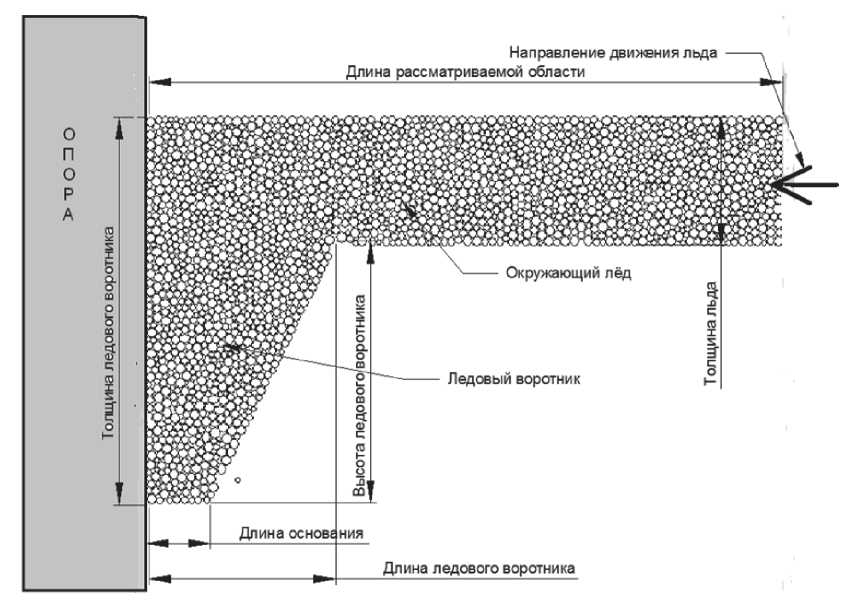
Рис. 2. Расчетная схема в вертикальной плоскости

Рис. 3. Иллюстрация причины резкого снижения уровня ледовой нагрузки (откол фрагмента): слева - до начала взаимодействия, справа - после взаимодействия

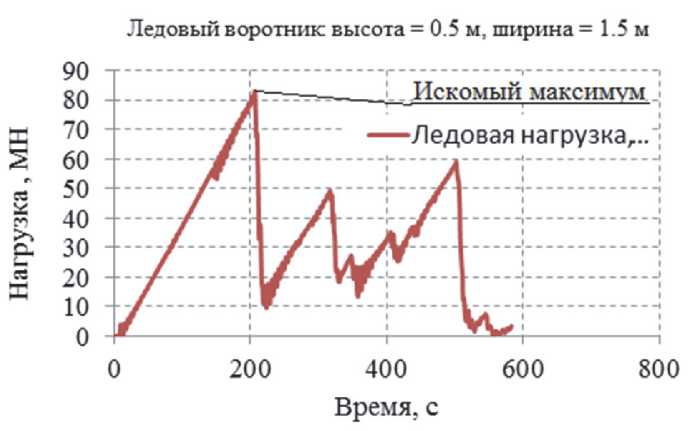
Рис. 4. Зависимость ледовой нагрузки от времени в ходе моделирования; показан максимум, используемый для дальнейших оценок

поле. Материал вокруг опоры (зона ледового воротника) имеет прочность, отличную от прочности окружающего льда. Начальная ширина зоны, включающая материал с другими свойствами, может варьироваться в заданных пределах.

В начальный момент времени поле начинает двигаться с заданной скоростью и нагрузки, действующие на опору, регистрируются. Задача решается в двумерной постановке в плоскости льда, поэтому размеры воротника и его влияние на нагрузки должно быть оценено специальным образом. Было принято, что зона материала с другими свойствами простирается до сечения, где толщина воротника совпадает с шириной ровного льда (на рис. 5 темная в центре). Протяженность области вокруг опоры можно определить исходя из следующей зависимости:

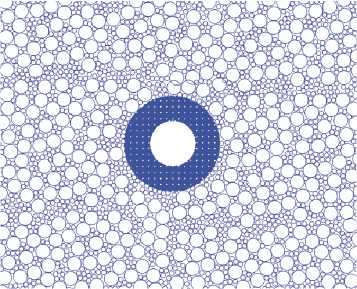
Рис. 5. Схема расчетного случая в горизонтальной плоскости (опора, зона с прочностью льда отличной от прочности окружающего льда вокруг опоры, окружающий лёд)

^ области    (^ льда " ^к   ^ льда ) " ^^^   ⁽¹⁾

где:

%_{области} - искомая протяженность зоны, принимаемой вокруг опоры, м;

^_льда — толщина окружающего льда, м;

к - коэффициент формы ледового воротника, показывающий во сколько раз толщина ледового воротника на опоре больше толщины окружающего льда;

а - угол, характеризующий форму ледового воротника (угол примыкания к опоре, отсчитываемый от вертикали).

Тогда эффективная прочность льда вокруг опоры, моделирующая ледовый воротник может быть определена по формуле:

^ й(области) ^F

^ к(льда)    ^F 1m

где:

^ й(области)

--------- - показывает во сколько раз ко-

^ й(льда)

эффициент прочности зоны вокруг опоры превышает рассматриваемый коэффициент прочности окружающего льда;

С д( _{области} ) - коэффициент прочности зоны вокруг опоры, МПа;

С д( _льда ) - коэффициент прочности льда, МПа (, по ИСО 19906 [25]);

F

--относительная нагрузка, получаемая

Fim при рассмотрении двумерного случая взаимодействия плоской стенки со льдом и ледовым воротником; (F-абсолютная нагрузка ото льда и ледового воротника; F1m- абсолютная нагрузка от ровного льда).

Эффективная прочность при сжатии льда в этой зоне определена из условия передачи на опору (при рассмотрении процесса в вертикаль- ной плоскости) той же нагрузки, что и передается при наличии ледового воротника. Таким образом, вычисленная окончательно нагрузка учитывает сумму явлений, проходящих в вертикальной (рис. 2) и горизонтальной (рис. 5) плоскостях. Значение, соответствующее разрушению ледового воротника, фиксируется для дальнейшей статистической обработки. Поведение нагрузки от времени аналогично представленному на рис. 4.

РЕЗУЛЬТАТЫ РАСЧЕТА

В качестве исходных данных рассмотрены массивы данных с различными входными параметрами: формы ледовых воротников и толщины льда, зависящие от морозоградусодней (МГД).

Количество экспериментов, для определения влияния на нагрузку, выбиралось из условия, чтобы относительная ошибка результата для каждой серии экспериментов не превышала 10%. В большинстве случаев фактическая относительная ошибка не превышает нескольких процентов.

Принята следующая последовательность вычислений: фиксируется несколько значений МГД, для них находится соответствующая толщина льда. Для определенной толщины льда, по полученным ранее зависимостям, определяются параметры ледового воротника k и а . Таким образом определяется значение нагрузки в зависимости от количества МГД. Нагрузка приводится к относительным значениям путем отнесения к нагрузке при соответствующей толщине ровного льда F/F_лёд . На рис. 6 представлен график зависимости относительной нагрузки F/F_лёд от количества МГД.

F - нагрузка на вертикальную стенку, вмерзшую в лёд, при наличии ледового воротника.

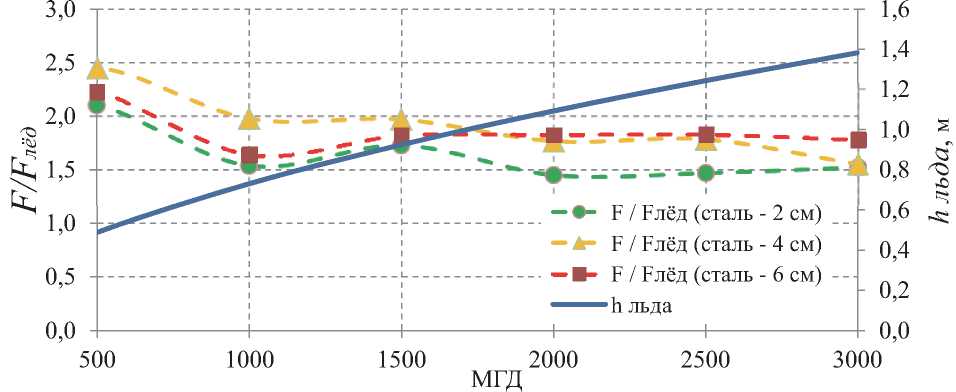
Рис. 6. Зависимость относительной нагрузки F/F_лёд и толщины ровного льда к_лёд от количества МГД

Р_лёд - нагрузка на вертикальную стенку от ровного льда заданной толщины.

Нагрузка на вертикальные цилиндрические опоры при наличии ледовых воротников определялась относительно случая прорезания льда опорой Рвв/Рд . Рвв - нагрузка на цилиндрическое сооружение, вмерзшее в лёд, при наличии ледового воротника; Рд - нагрузка на цилиндрическое сооружение в дрейфующем льде (за опорой образуется канал вследствие прорезания льда);

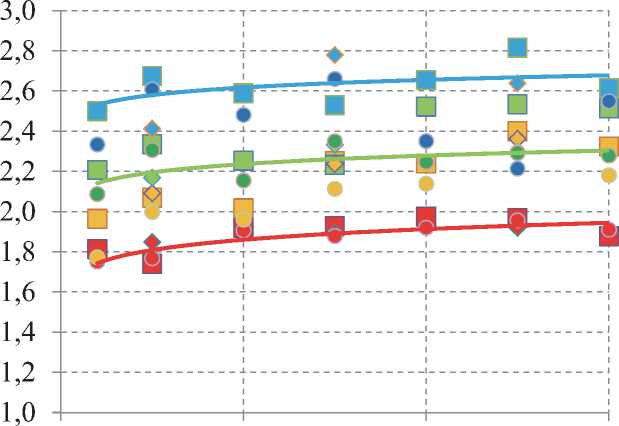
На рис. 7 представлены зависимости нагрузки на опору при наличии ледового воротника по отношению к случаю прорезания опоры через лёд, для различных диаметров опоры в зависимости от количества МГД.

Данные, представленные на рисунках выше, были получены путём задания диаметра сооружения и дальнейшего изменения всех связанных параметров в зависимости от МГД. При изменении МГД меняется также и толщина ровного льда. Для некоторых целей может представлять интерес зависимость нагрузки от отношения диаметра сооружения к толщине льда. На рис. 8 представлены графики зависимости относительной нагрузки Рвв/Рд для разной толщины стали в зависимости от отношения диаметра опоры к толщине ровного окружающего льда D/h_льда .

О

мгд

• ■    D=40 м (сталь 6 см)

• □    D=10 м (сталь 6 см)

• □    D=5 м (сталь 6 см)

• ■    D=2 м (сталь 6 см)

• ♦    D=40 м (сталь 4 см)

О D=10 м (сталь 4 см)

• ♦    D=5 м (сталь 4 см)

• ♦    D=2 м (сталь 4 см)

• •    D=40 м (сталь 2 см)

• •    D=10 м (сталь 2 см)

• •    D=5 м (сталь 2 см)

• •    D=2 м (сталь 2 см)

Рис. 7. Зависимость относительной нагрузки на опору Рвв/Рд от МГД для различных диаметров опоры (на легенде)

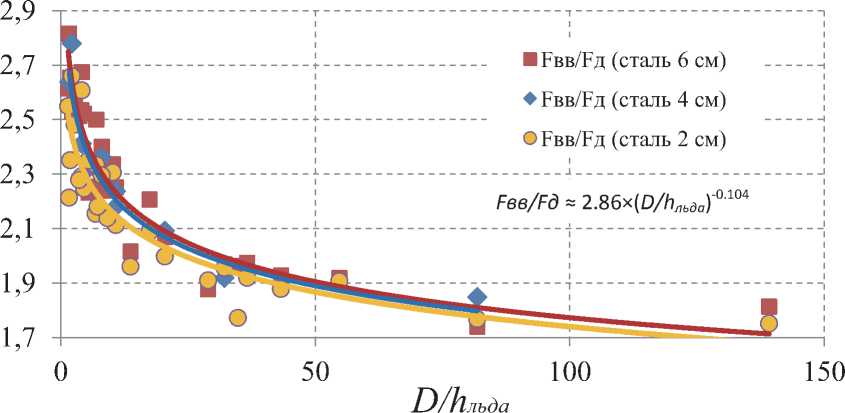
Рис. 8. Зависимость относительной нагрузки на опору Рвв/Рд от отношения диаметра опоры к толщине ровного льда D/ ^_льда (для разных толщин стали)

ВЫВОДЫ

В ходе проделанных экспериментов было установлено, то уменьшение диаметра опор, приводит к увеличению относительного влияния ледового воротника.

При малом диаметре опоры наличие воротника может увеличить нагрузку до полутора раз по сравнению со случаем, когда воротника нет. Нагрузка при наличии ледового воротника может превзойти нагрузку от дрейфующего льда более чем в два раза.

При больших диаметрах сооружений влияние воротника существенно меньше (10-12%) по сравнению со случаем отсутствия воротника. Однако различие в нагрузках характерных для дрейфующего льда остается большим.

Влияние морозоградусодней на нагрузку составляет около 10-15% от общего увеличения.

Прослеживается довольно четкая зависимость от отношения диаметра опоры к толщине ровного льда, образовавшегося в тех же условиях, что и воротник.

При дальнейшем увеличении диаметра сооружения (более 20 м) нагрузки мало меняются по сравнению с нагрузкой на опору диаметром 40 м.