Определение направления и скорости конвективных потоков воздуха с помощью воздушного шара на цепи
Автор: Лохов Сергей Прокопьевич, Фаида Евгений Леонидович, Варганов Виталий Викторович
Журнал: Вестник Южно-Уральского государственного университета. Серия: Энергетика @vestnik-susu-power
Рубрика: Теплоэнергетика
Статья в выпуске: 9 (49), 2005 года.
Бесплатный доступ
Поместив в слабый конвективный поток воздуха наполненный гелием детский воздушный шар на тяжелой гибкой связи (цепочки от карманных часов), можно сравнительно просто и достаточно точно определить направление и скорость потока. Цепочка позволяет измерять малые усилия потока на шар, ей не свойственно сухое трение. Для расчетов используются формулы аэродинамики шара и уравнения цепной линии. Приведены результаты эксперимента.
Короткий адрес: https://sciup.org/147158003
IDR: 147158003
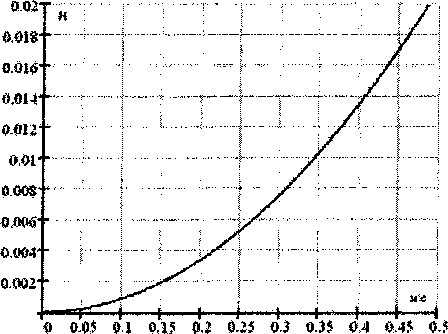
Список литературы Определение направления и скорости конвективных потоков воздуха с помощью воздушного шара на цепи
- Математическая энциклопедия. -М.: Советская энциклопедия, 1985. -Т. 5. -1248 с.
- Алътшуль А.Д., Кисилев П.К. Гидравлика и аэродинамика. -М.: Стройиздат, 1965. -407 с.
