Определение напряженно-деформированного состояния при прессовании трубы

Исходя из вариационных принципов механики сплошных сред, если известны поля скоростей, то путем их дифференцирования легко определяются поля скоростей деформаций [1, 2]. Поля напряжений могут быть получены в дальнейшем из уравнений статики и связи, в качестве которых можно использовать уравнения теории течения или теории деформаций. Известные методы в большей или меньшей степени связаны с необходимостью проведения экспериментов, например, для апрок-симации условий течения. В данной работе сделана попытка описать деформированное состояние чисто аналитическим путем.

Аналитический метод применен для осесимметричной деформации при прессовании круглой трубы с неподвижной иглой из полой заготовки. После скоростей для данного процесса определим через интегрирование условия неразрывности материала заготовки при заданных граничных условиях методами математической физики [3]. В цилиндрической системе координат (r, φ, z) геометрический очаг пластической деформации опишем в виде полого цилиндра высотой h и радиусами R 0 и r 0 . Схема процесса деформирования представлена на рис. 1. Пусть в области пластического течения задан потенциал скоростей U (r, z), связанный с вектором скорости соотношением

V = gradU(r, z)

или в координатной форме

V = S- V = £

Если в очаге деформации отсутствуют источники, стоки и завихрения, то условие несжимаемости можно записать в следующем виде d2U 1 dU_ d2U dr2 r dr dz2

Из условия симметрии дифференцирование по φ опущено. Граничные условия на контуре очага деформации

■dU ।     = dU |r=R = о dr r ro    dr r ^0

dU .

dz ^lz = ^h

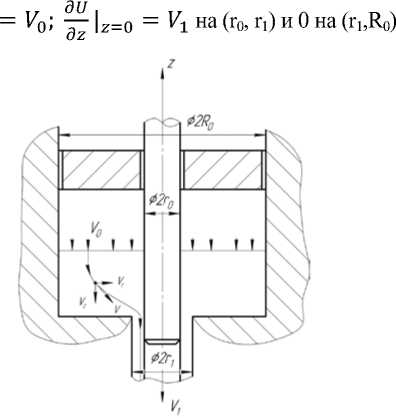
Рис. 1. Схема очага пластической деформации при прессовании трубы

Задание уравнения (2) и граничных условий (3) определяет потенциал U (r,z) однозначно с точностью до постоянного слагаемого. Для отыскания потенциала скоростей используем конечные интегральные преобразования [3], которые предполагают исключение операции диф-ференцирования по r, обращение уравнения (2) в обыкновенное дифференциальное уравнение. Найдем ядро преобразования, позволяющее исключить дифференциальные операции по z из решения уравнения

d2d + 1aA + ^kK = 0

dr2 r dr ^

и граничного условия dr \r=o    dr |r=Ro    0        (5)

Подчинив общее решение AI 0 (A_kr) + BN 0 (A_kr) уравнения (4) условиям (5), получим

-AA^A^) - BA_kN i (A_kro) = 0

-AAjMA k Ro) - BA k NAA k Ro) = 0      (6)

Чтобы существовали решения, отличные от тривиального решения A = B = 0, определитель

I I i (A k r o )   N 1 (A k r o )\

Vi№) N1(AkR0)\ должен быть равен нулю, что для определения собственных чисел дает уравнение

I i (A k ro)N i (A k Ro) - N i (A k ro)I i (A k Ro) = 0

Решив систему (6), найдем, что с точностью до произвольного множителя

A = -N i (A_kT o ),   B = I i (A k r o )

Таким образом, можно принять

K k ⁽ r) = I⁽A k r)N o ⁽A kr) - N i ⁽A k r o) I o ⁽A kr)

Нормирующий множитель C k равен

R o

Г                                             „          2     I₃ (A_kr₀ ) — I₃ (A_kR")

C k = J [I i (A k r o )N o (A k r) -N i (A k r o )I o (A k r)]²rdr = ^2 • ^1V p^R^

r0                                                                k         1

Осуществив в интервале r0 < r < Ro преобразование с ядром — • Kk(r"), приведем задачу (2), (3) к Ск виду

^-A^U = 0

dz2 kv 7

Ro dU,       Vo f , s „ у\z=n = 7- I Kk(r)rdr = 0 dZ        Ck J

Ro dUV dZ\z=o = q^ J Kk(r)rdr =

r0

V3r3

7— ^[I⁽A k r o )N i ⁽A k r i ) - N i ⁽A k r o) I i ⁽A k r i)A ^C k ^A k

_^^

= V i

Общее решение уравнения (7) условиях (8)

при граничных

Применяя формулу обращения, получим искомое решение в виде сходящегося ряда

U_o = -V_oz + const

к = 0

V i chA k (h-z)

^Uk = at;

^^

chAkh

к > 0

U⁽r, z) = U o + ^ Uk" K k (r) k=i

^U(r,^Z) = ^-V o ^z + T. k=i ^V1C^_k^_kh^{Z) K} k ^(r) + ^const

Взяв градиент от потенциала (9) получим непрерывное кинематически возможное поле скоростей для прессования трубы:

V z

V o

-

i-2

V_ishA_k (h - z)

Vr   Y’o

V 0 = ^ ^k=ⁱ

— k=i,  .

V₁chC_k(h-z) C_kshC_kh

shAkh

^K k ^(r)

^K k ^(r)

V = ^W² + V z² ,

. Vr Ф = arctg — ^V z

Компоненты тензора скоростей деформаций в каждой точке зоны пластической деформации можно определить по формулам:

. _ d²U   . _ 1 dU

^^r   dr² ’ ^ ф   r dr ’

. _ d²U    . _ _? d²U

^£z = dz 2 ’ ^Yrz = ² drdz

Компоненты тензора напряжений могут быть определены из уравнений равновесия, записанных в цилиндрической системе координат, соотношений между напряжениями и скоростями деформации и условия пластичности Мизеса. В результате получим

, ^-r-^-z

O r = О z ⁺--A--

^- m — ^- 7

О ф = O z +                  (12)

C

Y rz

Trz 2A

Так как рассматривается установившийся процесс, то компоненты напряжений являются функциями только координат

do_z = ^dr^£ dr + ^d —^L dz ^z dr       dz

Интегрируя выражение (13) от какой-либо точки виде

(r0, z0), получим осевой компонент напряжения в oz (r- z)  f frf-1-^)-^©-"^^!^-

J r₀P^r\   2 dz \2Л/     22 J

-$XQS) ⁺(S)]^{dz+ a} * ^(t « ' ^z " )               ⁽¹⁴⁾

Величина (7z(r0, z0) может быть определена из условия равенства нулю результирующей силы в выходном сечении.

На рис. 2 показано распределение осевых сжимающих напряжений в области очага пластической деформации, полученных расчётом на ЭВМ при прессовании свинцовой заготовки с коэффициентом вытяжки, равным 3,5. Полученная картина течения достаточно близка к экспериментальной [4].

Выражения (10), (11), (12), (14) представляют основные уравнения, описывающие напряженно-деформированное состояние при прессовании трубы. Решение этих уравнений при заданных граничных условиях по напряжениям и скорости, а также по известной зависимости между интенсивностями напряжений и скоростей деформаций, получаемой из опытов на растяжение или сжатие для конкретных материалов, является полным решением исследуемой задачи.

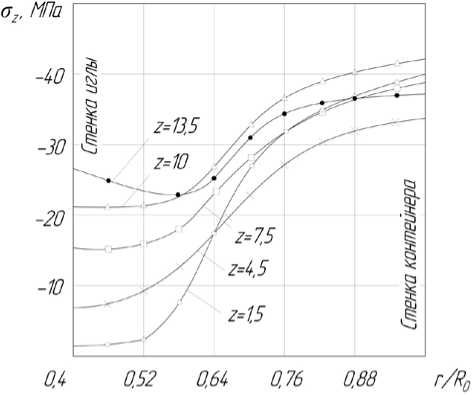
Рис. 2. Характер распределения осевых сжимающих напряжений в очаге пластических деформаций