Определение напряженно-деформированного состояния резиновых элементов внутренней амортизации опорного катка гусеничного движителя

целью представленной работы является разработка алгоритма расчета напряженно-деформированного состояния резиновых элементов опорного катка с внутренней амортизацией.

В настоящее время известно достаточно много конструкций опорных катков с резиновыми элементами. Тем не менее, из всего многообразия можно выделить три основные группы конструктивных решений. Первое связано с использованием наружного резинового бандажа на опорном катке. Второй вариант предусматривает эластичную связь между ступицей и наружным бандажом опорного катка за счет сплошного резинового или резинометаллического элемента выполненного в виде колец различных форм. В третьей группе конструктивных решений связь между наружным бандажом и ступицей осуществляется с помощью резинометаллических шарниров различных типов. Опорные катки с внешней ошиновкой нашли широкое применение в быстроходных гусеничных машинах, в которых, как правило, используются так называемые катки большого диаметра и к долговечности элементов предъявляются не такие жесткие требования как к элементам ходовой части сельскохозяйственных гусеничных тракторов.

Применение резиновой ошиновки опорного катка позволяет снизить динамические нагрузки на элементы гусеничного движителя (беговую дорожку трака и каток), повышая этим срок службы гусеницы и подшипников опорного катка, а также предохраняя от разрушения и сам каток. Особенно проявляется это преимущество при движении на транспортных режимах с большими скоростями по твердым каменистым грунтам и булыжнику. Однако условия работы резиновых шин достаточно тяжелые [1, 2]. При качении опорного катка по гусеничному полотну резиновая шина испытывает значительные деформации, которые носят циклический характер, в результате происходит саморазогрев резины, что приводит к термомеханическому разрушению. Кроме того, внешняя шина подвержена износу и не защищена от воздействия агрессивной среды (озона, солнечных лучей, масел) и инородных предметов.

В опорных катках с внутренними резиновыми элементами резина работает в более благоприятных условиях [1, 2], а именно: большая ее часть защищена от воздействия агрессивной среды, резиновые элементы воспринимают деформации сжатия и сдвига, резина защищена от прямого воздействия инородных предметов, попадающих между гусеничным полотном и опорным катком. Все это позволяет значительно увеличить долговечность резинового элемента. Еще одним положительным свойством конструкций опорных катков с внутренними резиновыми элементами является их ремонтопригодность. В таких конструкциях наименее долговечными являются как сами резиновые элементы, так и наружный бандаж, замена которых при ремонте гусеничного движителя, для некоторых конструкций, возможна без демонтажа всего опорного катка. На рис. 1 представлены результаты расчета динамической нагрузки, действующей в области контакта бандажа и беговой дорожки для цельного стального опорного катка и для конструкции с микроподрессориванием для сельскохозяйственного трактора класса 3. Определение динамической нагрузки осуществлялось в соответствии с методикой, предложенной В.Ф. Платоновым [3]. Результаты расчета (рис. 1) показали, что применение предложенной конструкции позволяет снизить динамическую нагрузку при скорости движения трактора 3 м/с в 1,76 раза, при этом общая нагрузка снижается в 1,25 раза.

Таким образом, в гусеничных движителях сельскохозяйственных тракторов для снижения динамических нагрузок при качении опорного катка по гусеничному обводу целесообразно использовать конструкции опорных катков с внутренними резиновыми элементами. В процессе эксплуатации резиновые элементы испытывают следующие виды деформации: большие начальные деформации, связанные с установкой и сборкой резиновых элементов в опорном катке, при этом резиновые элементы могут испытывать сжатие по торцовой поверхности, напрессовку по внутреннему радиусу, запрессовку по внешнему радиусу. Резиновые элементы могут быть выполнены в виде чисто резиновых элементов или в виде резинометаллических, т.е. имеющих металлическую арматуру.

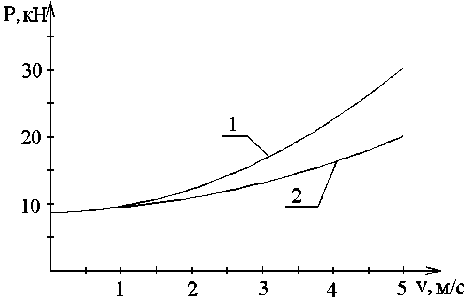
Рис. 1. Силы, действующие в паре «бандаж опорного катка – беговая дорожка звена» с учетом статической составляющей: 1 – стальной опорный каток; 2 – опорный каток с внутренней амортизацией

При движении по беговой дорожке гусеничного полотна опорный каток испытывает ударные и динамические воздействия в радиальном направлении, связанные со звенчатостью цепи и с вертикальными колебаниями корпуса гусеничной машины [3, 4]. Обеспечение надежной работы при данном виде нагружения требует расчета характеристик напряженно-деформированного состояния при радиальном нагружении. Конструкция резинового элемента должна обеспечивать при радиальном нагружении катка малую величину эксцентриситета, т.е. резина при данном виде нагружения должна испытывать только малые деформации, в противном случае (большая величина эксцентриситета) резко возрастают потери на внутреннее трение, что приводит к саморазогреву и быстрому выходу резиновых элементов из строя и к низкому моторесурсу.

Таким образом, задача расчета напряженно-деформированного состояния включает два этапа:

• -    расчет резиновых элементов при больших деформациях связанных со сборкой опорного катка;

• -    расчет малых деформаций при вторичном нагружении с учетом больших начальных деформаций.

Наиболее рациональным является применение конструкций опорных катков с резиновыми элементами, работающими на сдвиг [2] при радиальном нагружении. На рис. 2 представлен один из возможных вариантов конструкции опорного катка [5]. Опорные катки с кольцевыми резиновыми элементами, работающими на сдвиг, обладают большой радиальной и малой осевой податливостью, что обеспечивает снижение динамических нагрузок в области контакта и исключает увод бандажа при движении.

При сборке катка резиновые элементы предварительно сжимаются в осевом направлении, что повышает их усталостную прочность, а равномерная нагрузка всего сечения кольца при сдвиге в сочетании с простой его конфигурацией существенно снижает вероятность появления мест с концентрацией напряжений. Конструкции опорных катков этой группы позволяют осуществлять дополнительную затяжку резиновых элементов в процессе эксплуатации. Кроме того, конструктивно можно обеспечить ограничение радиальной деформации, что позволяет предохранить резиновые элементы от перегрузки.

В настоящей работе для оценки напряженно-деформированного состояния резинового элемента внутренней амортизации опорного катка (рис. 2) гусеничного движителя применяется алгоритм расчета, в основу которого положены соотношения нелинейной теории упругости для несжимаемого материала. Нелинейные соотношения между напряжениями и деформациями в резине описываются потенциалом внутренних сил, являющимися функциями первого и второго инвариантов тензора деформаций Коши. Для области упругих деформаций наиболее общий закон деформирования, выраженный через потенциал W , можно представить в форме [6]:

9W ti = — + PGi д у

,

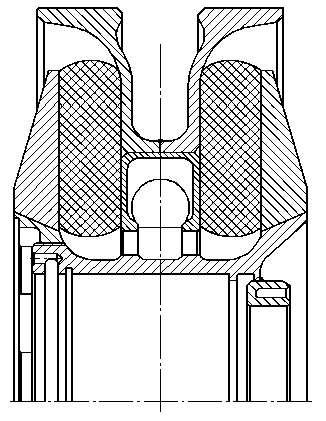
Рис. 2. Конструкция опорного катка с внутренней амортизацией

где P - функция гидростатического давления, определяемая из уравнений равновесия.

Механическое поведение резины описывается потенциалом Трелоара [7].

W = 2 Ц11 - з)

где и - модуль сдвига резины, I 1 - первый инвариант тензора меры деформации Коши.

Функционал потенциальной энергии системы для несжимаемого материала имеет вид

П "Ш

v

2(I1 - 3)+ Р(т - 1) dv — и Fu ds

s

, (3)

Конструктивные параметры резиновых элементов внутренней амортизации опорного катка до и после сборки в совокупности с нагрузками, действующими на каток во время эксплуатации, определяют их напряженно-деформированное состояние. В свою очередь, напряженно-деформированное состояние резиновых элементов в совокупности с режимами нагружения опорного катка определяют долговечность резиновых элементов. Таким образом, для оценки работоспособности опорного катка с внутренней амортизацией необходимо знать напряженно-деформированное состояние резиновых элементов.

где т = V / v ; V - деформированный объем; v - не-деформированный объем; s - поверхность объема v ; p - функция гидростатического давления; F , й - соответственно вектор сил и вектор перемещений на границе области, где заданы внешние силы.

Силовые резиновые и резинометаллические элементы внутренней амортизации являются телами вращения, в связи с этим рассмотрим конечные деформации в цилиндрической системе координат. Положение точки в цилиндрической системе координат определяется:

- в недеформированном состоянии r , ^ф , z ;

- в    деформированном    состоянии

R = R(r, ф, z) 0 = ©(r, ф, z) Z = Z(r, ф, z)

,                                            ,                                            .

Первый инвариант тензора меры деформации Коши в цилиндрической системе координат

Т — Р ² I Т?2^ ² I 7 ² I ¹ (Р ² I /?2^ ² I 7 ²Vp²_i_Z?2rA ² I 7 ²

1 1 = ^R r ⁺ R ^W r ⁺ Z r ⁺ — ( R ф ⁺ R ^У ф ⁺ Z ф ) ⁺ R z ⁺ R ^У z ^{+ Z} z

r

Здесь и далее нижний индекс означает частную производную по соответствующей координа- те.

Компоненты тензора напряжений Коши для потенциала Трелоара:

n 2     1 n 2 _n

C, =Ц R, +—Rф

r r-T 2      1

C z = M Zr + r2 Zф

z

z

О ф -t- R ² 0 r ² + r 2 0 ф² +0.?

+ p

;

+p

;

+p

;

т rz = ц Z , R , + A Z ф R ф + Z z R z

• -    в промежуточном состоянии R ⁰ = r + u ⁰ ( r , z ) , 0 0 =ф , Z ⁰ = z + w ⁰ ( r , z ) , P ⁰ = P ⁰ ( r , z ) ;

• -    в конечном состоянии R = R ⁰ + n u ( r , z ) , 0 = ф , Z = Z ⁰ +n w ( r , z ) , P = P ⁰ + n p ( r , z ) , где u, w – функции радиального и осевого перемещений.

С учетом принятых допущений функционал приращения потенциальной энергии при деформировании резинового элемента в процессе сборки запишется в виде:

T r Ф

T z ф

;

,' R R r 0 r + -L R ф 0 ф + R z 0 z

= ^ R ⁰ , ^Z , ⁺ r 2 ⁰ ф ^Z ф ⁺⁰ _:2 :

;

—^{[ u} 2 ⁺ w ^{2 +} — ⁺ H z ⁺ w^{2 ]+} 2 r

+ ( P ⁰ u_ + PR ) x ( u, Z 0 + R 0 w z - wR - Z 0 U z ) + rr

+ P ⁰ —( u _r w _z - u _z w _r ) + P— ( R r Z z - Z 0 R z ) I dv - r                     r

- fj(Fru + Fzw)ds s                                   (6)

В соответствии с алгоритмом метода, предложенного в работах Лавендела Э.Э., Дым-никова С.И. непрерывный процесс деформирования резинового элемента заменяется пошаговой процедурой. На каждом шаге решения нелинейной задачи применяются линеаризованные соотношения нелинейной теории упругости. Таким образом, на каждом шаге решается линейная задача, но при этом учитывается напряженно-деформированное состояние, возникшее в резиновом элементе в результате деформации на предыдущих шагах деформирования. Вариация приращения потенциальной энергии на каждом шаге деформирования определяется выражением:

5(АП) = 8( jWdv-1 jAF-Айds )

^{v 2 s}                 ,     (5)

1 d ²

где ^W = 2 dn 2 ^[ W + ⁽ - ^)(т- ^)] ; W — упругий потенциал Трелоара; n - малый параметр; A T ? , A d - соответственно приращение вектора сил и вектора перемещений на границе области, где заданы внешние силы.

Сжатие резиновых элементов в осевом направлении при сборке катка рассматривается как осесимметричная задача нелинейной теории упругости. Большие деформации резины, связанные со сборкой определяются координатами:

• - в начальном состоянии ^r , ^ф , ^z ;

Компоненты тензора напряжений Коши для потенциала Трелоара определяются следующими соотношениями:

^C r =^ [ ^R r ^{2 + R} z ² ] + P ; ^C z =^ [ Z r ^{2 + Z} z ² ] + P ;

R ²

^Сф"^{Ц     + P} ; T rz =ц [ Z r R r + Z z R z ] .   (7)

При вторичном нагружении радиальной силой положение точки в недеформированном, промежуточном и конечном состояниях обозначаются соответственно:

r ф z -R ⁰ = R ⁰ ( r , ф , z )     0 0 =0 0 ( r , ф , z )

,,;               ,

Z ⁰ = Z ⁰ ( r , ф , z ).

;

R = R0 + nu (r, ф, z)    0 = 00 + рф( r, ф, z)

,,

Z = Z0 +n w (r, ф, z ).

;

искомые функции перемещений являются функциями координат недеформированного состояния.

Приращение потенциальной энергии системы при наложении малых упругих деформаций на конечные при вторичном нагружении радиальной силой записывается в виде:

АП= [ff|- [ u 2 + R ⁰ 2 Ф 2 + 4 R ^o0 0 u Ф_г+0 ° u ² + w, 2 + 2 ^{r r r r r r} v

+ 1L (u ф + R °²ф ф + 4 R °0 ф u Ф ф +0 ф u ² + w 2 ) + u z + r

+ R02Ф2 + 4R000uФz +002u2 + w2]+(P0 u + PR- )x rr x (u zZ00" + Rrwz0" + RZX -ФфzrRz1 -0"wrRz1 -00 r70         0OrxO n 0   z"\0 n 0^0/га        п0/~\0

" Z_Tu_z + ^u " Z, ⁰ z + ^R " w r ^{0 + R} " Z^ z - w z^R . ⁰ Г -yOnO/r, , /^O^yO , r>O>Fx i

^{- Z}z ^R „ ^Ф T ^{+ u}z ⁰ T Z " ^{+ R}z ^Ф r^Z "+ ^R= ⁰ T w " — ^UT^Z "⁰ z -

- Z° z U " 0 0 - R T w " 0 0 - R T Z⁰" Ф z ) + P ⁰ — ( u r W z 0 " + r

+ и Z°O + R°w Ф — 0°w и — Z°O и — Л°Ф w + ^И T z "  T ^,kz "       "  T^z      T "  z z^_z "' r_r

+ R> T Ф z + Z T U " Ф z +0 0 u " Wt - Zz°u " Ф T - R> z Ф T -- 0 0 W z u " + R z ⁰Ф r W " + 0>_zw " + Z 0 u_z Ф r - R 0 w " Ф z -- ^Z u ^Ф z ^{- 0} 0 ^uT^W " ) । dv ^- jj ⁽ F T^{u + F} P ^{Ф R 0 + F}z ^w ) ds s

При реализации алгоритма с помощью метода конечных элементов используется пошаговая процедура, позволяющая учитывать изменение граничных условий в процессе нагружения резинового элемента [7]. Решение задачи по определению напряженно-деформированного состояния после сборки, вызванного сжатием в осевом направлении, осуществляется в цилиндрической системе координат, рассматривается осесимметричная задача, дискретизация сечения резинового элемента выполняется изопарамет-рическими конечными элементами с восьмью узлами и нелинейной аппроксимацией перемещений. При последующем нагружении радиальной нагрузкой задача рассматривается в цилиндрической системе координат и для ее решения применяются объемные изопараметрические конечные элементы с двадцатью узлами.

а)                  б)

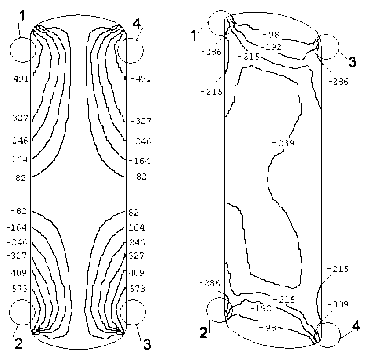
Рис. 3. Картины распределения касательных напряжений (кПа) по сечению резинового элемента вызванных: а – сборкой; б – радиальной силой

В результате расчета получены поля распределения компонентов тензоров деформаций, напряжений и удельной энергии деформации по объему резинового элемента. На рис. 3 представлены картины распределения касательных напряжений, вызванных сборкой и последующим нагружением радиальной силой. Максимальных значений касательные напряжения, вызванные сборкой для рассматриваемой конструкции действуют в областях 1 и 4, 2 и 3 (рис. 3а) и составляют соответственно 0,655 МПа и 0,732 МПа. При вторичном нагружении радиальной силой максимальные значения касательных напряжений действуют в областях 1 и 4, 2 и 3 (рис. 3а) и составляют: - 0,333 МПа в области 1 и 3; - 0,309 МПа в области 2; - 0,356 МПа в области 4.

Выводы: максимальные значений касательные напряжения достигают как при сборке, так и при вторичном нагружении в одних и тех же областях, т.е. в крайних точках контакта резинового элемента с поверхностями обода и ступицы опорного катка, следовательно, и начало усталостного разрушения для элементов данной конструкции будет наблюдаться в этих областях.