Определение напряженного состояния и усилия деформации шарообразных заготовок в закрытой матрице

ВЕСТНИК ПНИПУ. МЕХАНИКА № 4, 2021PNRPU MECHANICS BULLETIN

Интенсификация исследований в области машиностроения и металлургии формирует потребность в технологиях, обеспечивающих новый уровень техникоэксплуатационных свойств металлоизделий. В первом упрощении, последнее регламентируется уровнем и соотношением прочностных и пластических характеристик. Известно [1], что существенного увеличения прочности металлов и сплавов можно достичь двумя основными путями:

• 1)    снижением количества несовершенств кристаллического строения;

• 2)    насыщением дефектами наноуровня, препятствующими движению дислокаций.

Стоит отметить, что наибольшую эффективность и распространенность при реализации второго метода упрочнения получили методы интенсивного пластического деформирования [2–10].

Материалы, полученные методами интенсивного пластического деформирования (ИПД), обладают повышенным уровнем прочностных характеристик [11, 12], достаточной пластичностью [13, 14], высокими коррозионной стойкостью [15, 16], ударной вязкостью, износостойкостью и др. [17, 18]. Такие материалы обладают, как правило, субультрамелкозернистой (СУМЗ) и/или наноструктурой [19, 20].

Внедрение инновационных методов ИПД в типовой технологический процесс получения различных металлоизделий уже имеет подтвержденный опыт. Однако эта интеграция связана с рядом ограничений. Основные ограничивающие факторы и пути их преодоления приводят авторы работы [21, 22]. В работе [23] выполнена оценка возможности интеграции технологии равноканального углового прессования в метизное производство. Авторами работы [24] ведется разработка группы импортозамещающих сплавов для производства ультрахладостойкого наноструктурированного листового проката, причем реализация технологии планируется на действующем толстолистовом стане 5000. Обработку методами ИПД трубных заготовок предлагают авторы работы [25].

Таким образом, разработка новых инновационных технологий, способных к эффективной интеграции в действующее производство, и обеспечивающих придание уникальных свойств получаемым материалам и металлоизделиям является актуальной, требующей поиска новых путей проблемой.

1.    Материалы и методы

Цель настоящего исследования заключается в разработке теоретического подхода к определению напряженного состояния и усилия деформации шарообразных заготовок в закрытой матрице.

Получение поковок с формой и размерам, максимально приближенной к форме готовых изделий, обеспечивает снижение затрат на производство металлопродукции. Следует отметить, что в формообразующих штампах невозможно реализовать многоцикловую обработку для получения качественных поковок и деталей. Поковки после горячей объемной штамповки имеют волокнистую структуру, часто на участках облоя наблюдаются перерезанные волокна. Поэтому для придания поковке и соответственно деталям требуемых свойств целесообразно применение предварительной многоцикловой обработки.

Широкое распространение в технике имеют изделия с утолщениями на одном или двух участках исходной заготовки, например заготовки с шарообразным утолщением с двумя отростками по краям. Для изготовления таких металлоизделий и в целях развития интеграции процессов наноструктурирования в промышленное производство решено использовать эффект взаимного влияния всестороннего сжатия и равноканального углового прессования (РКУП) в ранее разработанном устройстве для реализации РКУП в закрытой матрице [26].

Закрытая трехканальная матрица для многоцикловой обработки исходных заготовок состоит из следующих элементов: обоймы (на рисунке не показана); сферических полуматриц 1 и 2 ; 3 – боковых пуаноснов; 4 – центрального пунсона (рис. 1).

Многоцикловая обработка заготовок в закрытой трехканальной матрице осуществляется следующим образом:

• а)    цилиндрическая заготовка 5 устанавливается в нижнюю полость полуматрицы 2 через верхнее отверстие полуматрицы 1;

• б)    затем верхним центральным пуансоном заготовка осаживается до заполнения полости полуматриц и вытекания излишка металла в боковые отверстия;

• в)    после штамповая оснастка кантуется на 90⁰, и вытесненный металл в боковые отверстия деформируется в обратном направлении, с вытеканием металла в верхнее отверстие полуматрицы.

2.    Описание эксперимента

Далее цикл деформирования повторяется до получения субультрамелкозернистой и/или наноструктуры.

В исследовании используются матрицы и заготовки со следующими размерами: радиус шара равен 15 мм, диаметры отростков равны d от = 20 мм, диаметр исходной заготовки d з = 20 мм.

Объем исходной заготовки V з определяем через объем шара V _ш, с учетом объемов отростков V _от, вытекающих в отверстия, т.е.

V з = V ш + V от ,

Отсюда объем исходной заготовки равен:

Vз = (4/3) πR3+3 (π/4) dотhот, где R радиус шара, который равен 15 мм, диаметры отростков равны dот = 20 мм, высота отростков составляет hот = 10 мм, тогда, подставляя эти значения, получим:

V з = 23550 мм³.

Принимая диаметр исходной заготовки d _з = 20 мм, высота исходной заготовки h з будет равна:

h з = V з / F з = 75 мм.

Таким образом, для обработки шарообразных заготовки принимаем исходную заготовку размерами d з = 20 мм, h _з = 75 мм.

Возможность получения заготовок с СУМЗ или НС можно предварительно спрогнозировать путем оценки напряженного состояния в очаге пластической деформаций при деформировании в закрытой трехканальной матрице.

Для этого строим поле линий скольжения (л.с.) в очаге пластической деформации заготовки в момент вытеснения металла в боковые отверстия матрицы (рис. 1).

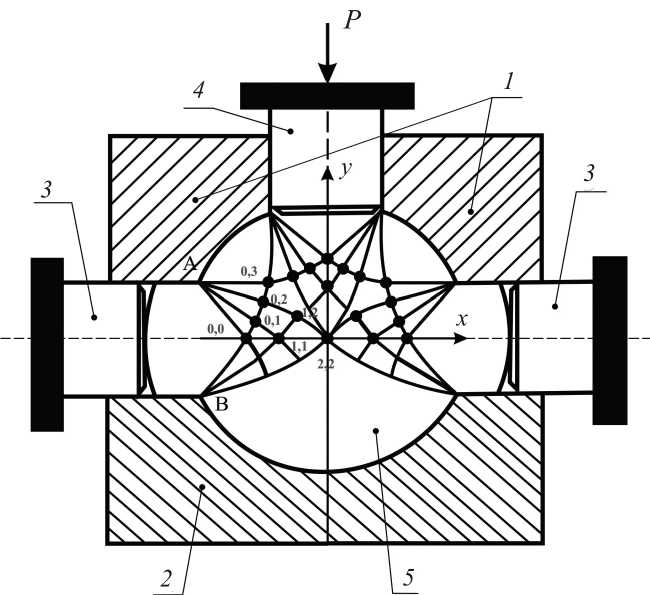
Рис. 1. Закрытая матрица для деформирования заготовки и поле линий скольжения в очаге пластической деформации: 1 – верхний полусферический штамп; 2 – нижний полусферический штамп; 3 – боковые пуансоны;

4 – верхний пуансон; 5 – заготовка

• Fig. 1. Closed matrix for deformation of the workpiece and the field of sliding lines in the focus of plastic deformation: 1 – upper hemispherical stamp; 2 – lower hemispherical stamp;

• 3 – side punches; 4 – top punch; 5 – blank

На выходе металла из очага деформации в боковые отверстия матрицы, т.е. на участке А и В, нормальные напряжения определим из следующего условия:

σ х = 0, σ у = –σ^* т .

Среднее напряжение на этом участке: σ ср = (σ х +σ у )/2 = = –0,5σ^* т , где σ^* т – сопротивление деформации металла при определенных деформационно-скоростных и температурных условиях.

Среднее напряжение в соседних узловых точках 0,1; 0,2 и 0,3 определим через соотношения Генки [27]:

σ0.i = σ00 – 2k (Δθ), где σ0.i – среднее напряжение в узловых точках 0.i поля л.с., i = 1,2,3…, например, σ01 и σ0.2 среднее напряжение вдоль узловых точек 0,1 и 0,2; k – постоянная пластичности или предел текучести на сдвиг; Δθ – шаг угла поворота л.с. при переходе от одной узловой точки к другой, например, при переходе из точки 0,0 в точку 0,1 шаг бу-π дет равен Δθ = θ0.1 – θ0.0 =12 рад., где θ0.1 и θ0.0 – соответственно углы наклона л.с. к главным осям в узловых точках 0,1 и 0,0. Отсюда среднее напряжение в узловой точке 0,1 составляет:

σ 01 = –0,5σ^* т – 2 k ( Δ θ ) , в остальных узловых точках :

σ_{0. i} = –0,5 σ^*_т – 2 k · ∆θ = –σ^*_т (0,5+ ₁ ^π ₂ ).

Постоянную пластичности k выразим через сопротивление деформации σ т ^*, т.е. через соотношение k = 0,5·σ т ^*. Сопротивление деформации определим через предел текучести материала σ т и соответствующие коэффициенты с помощью соотношения: σ т * = σ т · n ε · n σ · n β , где n ε – деформационный коэффициент, n _σ – коэффициент, учитывающих схему напряженного состояния, n β – коэффициент, учитывающий схему плоского деформированного состояния, равный 1,15 (коэффициент Лодэ). Предел текучести алюминиевой заготовки принимаем в пределах 57–63 МПа. Тогда, умножая соответствующие значения коэффициентов на σ т , получим:

σ т ^* = 63·1,5·1,4·115, = –152,145 МПа.

Отсюда среднее напряжение в узловых точках 0,1; 0,2 и 0,3 после подстановки значения сопротивления деформации составит:

σ 0.1 = –σ^* т (0,5+₁ ^π ₂) = –115,8 МПа,

σ 0.2 = –σ^* т (0,5+ ₁²₂ ^π ) = –178,57 МПа,

σ 0.3 = –σ^* т (0,5+ ₁ ³ ₂ ^π ) = –195,50 МПа.

Анализ результатов показывает, что в очаге деформации превалируют сжимающие напряжения, что способствует интенсификации пластической деформации и прогнозирует эффективное измельчение зерен металла. При этом средние значения напряжений в зонах заготовки от выхода в боковые каналы матрицы и до центральной зоны заготовки увеличиваются. Возникновение в очаге деформаций, в частности в центральной зоне, сжимающих напряжений вполне справедливо, так как металл будет находиться в состоянии всестороннего сжатия со стороны стенок матрицы. Сочетание эффекта всестороннего сжатия и углового выдавливания металла в боковые каналы матрицы способствует получению СУМЗ и НС заготовок.

Следующим этапом исследования напряженного состояния металла при деформировании в закрытой матрице является компьютерное моделирование. На рис. 2 приведены результаты компьютерного моделирования процесса деформирования заготовок в трехканальной закрытой матрице. Из данных рис. 2 можно заметить идентичность формы очага деформации, построенного методом линий скольжения и полученного компьютерным моделированием. Значения средних напряжений, полученные методом линий скольжения и компьютерным моделированием, находятся в сопоставимом диапазоне и показывают хорошую сходимость. В очаге деформации превалируют сжимающие напряжения со значениями –63 ÷ –192 МПа. Такой характер напряженного состояния является благоприятным для эффективного измельчения зерна в результате деформирования и, следовательно, улучшения комплекса механических и эксплуатационных характеристик получаемых металлоизделий.

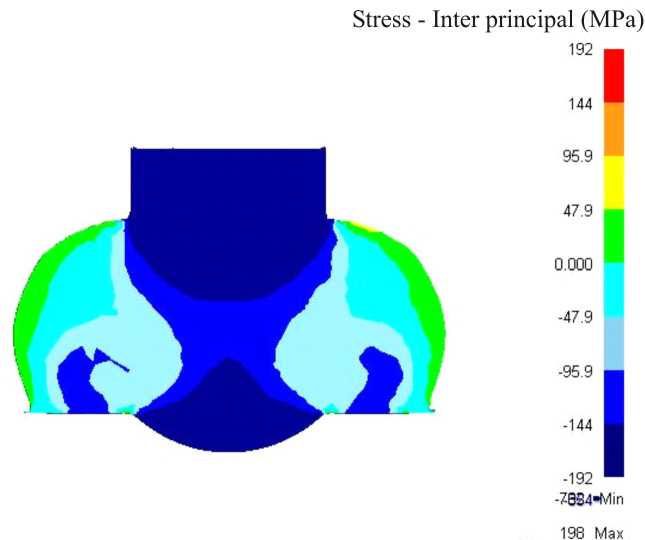
Рис. 2. Распределение среднего напряжения в очаге деформации, полученное компьютерным моделированием

• Fig. 2.    Distribution of mean stress in the deformation zone, obtained by computer simulation

Следующей задачей настоящего исследования является определение деформирующего усилия при деформации в закрытой матрице. Деформирующее усилие определяем в момент вытекания металла в боковые каналы матрицы, т.е. после заполнения всей полости матрицы металлом за счет воздействия верхнего пуансона, расположенного в верхнем отверстии полуматрицы.

Определение усилия деформирования на начальной стадии процесса нецелесообразно, так как на этой стадии осуществляется осаживание заготовки до полного заполнения полости матрицы и вытекания металла в боковые отверстия, в связи с чем усилие на начальном этапе деформирования будет недостаточным для преодоления сопротивления деформации на конечном этапе. Для определения усилия деформирования применим метод совместного решения дифференциальных уравнений и ус- ловия пластичности [28]. Решение производим по методике А. Целикова, изложенное в работе [29], для определения контактных напряжений и усилия прокатки.

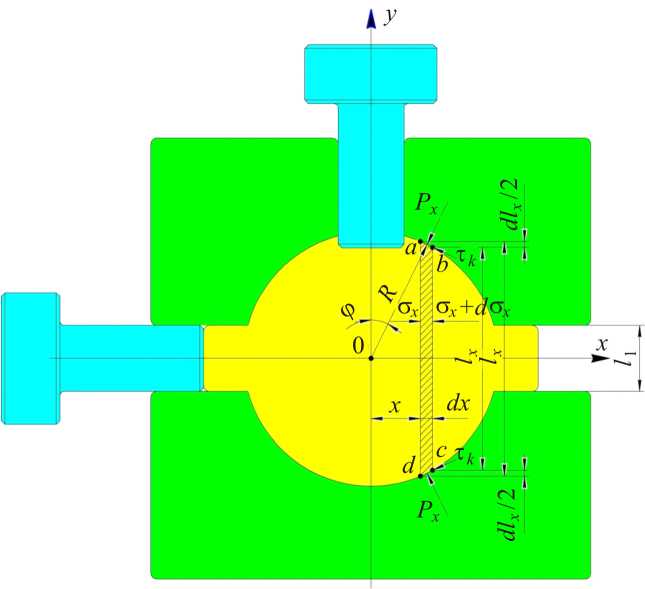
Рис. 3. Условия равновесия элемента abcd при определении усилия деформирования заготовки в закрытой матрице

• Fig. 3.    Equilibrium conditions for the abcd element in determining the deformation force of the workpiece in a closed matrix

Из уравнения равновесия элемента abcd (рис. 3), можно записать следующее:

Σx = 0. σх* (lx+ dlx) – (σx+ dσx)*lx – 2τкcosφ   x – cosp

2 p x sinφ ^dx = 0, где * ( l x + dl x ) = L x (рис. 3).

cos p

Раскрывая скобки, пренебрегая бесконечно малыми высшего порядка и после преобразования, получим:

σ _xdl_x – d σ _xl_x – 2τ_к dx – 2 p_x tgφ dx = 0.

dl

Учитывая, что tgφ = ^х и τ = fр получим: 2 dx

σxdlx – dσxlx – 2fрхdx – 2px dlх dх = 0, сократив на lx: 2dx dl σx x lx

2 fР dx    dl

– d σ x –     ^х   – р x ^x

I ■ / хx

= 0.

Заменяя дугу элемента хордой, из следующего гео метрического соотношения l ~ R - 0,5—x, определим R dx = - ^x^ , где 2R = D - диаметр обрабатываемого l1

шара, можно записать следующее:

dl             D dl      dl

σ x ^x – dp x + 2 fр х      ^x – р x ^x = 0.

l x                        l 1 l x            l x

2 fD

Вводя следующее обозначение: s =     , а также ис- l1

пользуя условие пластичности: px – σx = σт*, которое после дифференцирования примет следующий вид: dpx = dσx, подставляя в предыдущее уравнение, получим следующее: dl              dl

(σ – р ) x – dp + р s = 0, после преобразова-lx                     lx ния можно представить так:

(рхs – σт*) x – dpx = 0, после разделения перемен-lx ных и интегрирования примет вид:

( р х s – σ т ^* ) = С 0 l_x^s .

Постоянную C 0 находим из следующих граничных условий: при l_x = 0,5 l ₁ , р_x = –σ_т^*, выражая его из последнего и подставляя в предыдущее уравнение, окончательно получим:

*

р х = –

^ ^т ( - + 1 ) (f) - - 1. sl

s

Таким образом, получили уравнение, описывающее распределение контактных напряжений для диапазона заготовки от области выхода металла в боковые отверстия полуматриц до контактной поверхности верхнего пуансона. Допустим, обрабатывается шарообразная заготовка диаметром D = 35 мм. Например, при lx = 0,511 = 0,5• 25 = 12,5 мм,px = - от* = - 174,5 МПа, при lx = R = 17,5 мм, f = 0,5, s = 1,4, контактное давление на верхнем пуансоне составит: рx = 354,5 ≈ 355 МПа. Тогда полное усилие деформирования шара в закрытой матрице составит P = px• Fk, где Fk = П(dп )2 - площадь контактной поверхности шара и верхнего пуансона.

Тогда Р = 355·0,785·25² = 174171,875 Н.

Полученное максимальное значение усилия деформирования на пуансоне (174171,875 Н), т.е. произведение контактного давления на пуансоне на площадь пуансона, хорошо согласуется со значениями контактного давления и усилия деформирования (179000–171000 Н), полученными компьютерным моделированием (рис. 4).

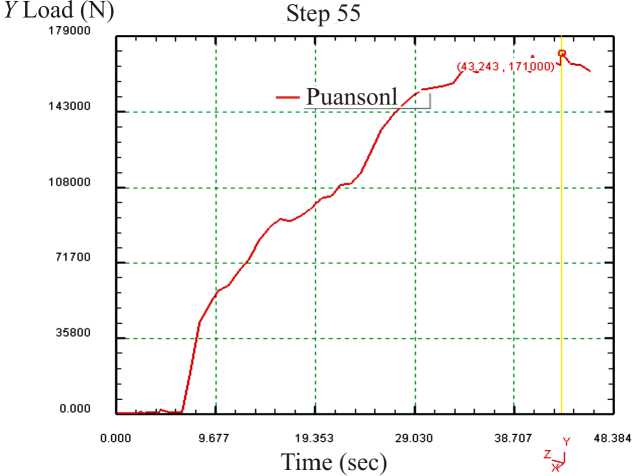
Рис. 4. Изменение контактного давления при перемещении пуансона

• Fig. 4.    Change in contact pressure by moving the punch

Для решения рассматриваемой задачи существует возможность использования вариационных и других математических методов, которые также хорошо себя зарекомендовали и показывают хорошую сходимость результатов, что отражено в работе [30].

Заключение

Выполнена оценка напряженного состояния заготовок (шаров) при всестороннем сжатии и угловом выдавливании металла в боковые каналы закрытой матрицы, определено деформирующее усилие заготовок на конечном этапе деформирования. Анализ результатов напряженного состояния заготовок, полученных методом линий скольжения, показывает формирование в объеме заготовки преимущественно сжимающих напряжений. Взаимное влияние условий всестороннего сжатия с угловым выдавливанием металла в боковые каналы матрицы прогнозирует получение заготовок с СУМЗ или НС.