Определение настроечных параметров процесса прошивки на двухвалковых станах винтовой прокатки

Определение настроечных параметров процесса прошивки является сложной комплексной задачей, при которой необходимо учитывать несколько взаимозависимых величин: расстояние между валками в пережиме, выдвижение оправки за пережим валков, расстояние между линейками, угол подачи и угол раскатки.

Для нахождения параметров настройки прошивного стана необходимо точно описать геометрические характеристики очага деформации в любом поперечном сечении. Данная задача легко решается без учета разворота валков на угол подачи [1] и применительно для работы прошивных станов на небольших углах подачи (до 6°) и в составе малых ТПА.

При ведении процесса прошивки на больших углах подачи пренебрегать искажением очага деформации из-за угла подачи недопустимо. При больших углах подачи фактическое расстояние между оправкой и валком в сечении формирования стенки гильзы больше, что приводит к получению более толстостенной гильзы, и обжатие перед носком оправки может быть меньше минимально допустимой величины, рассчитанной из условия вторичного захвата. Кроме изменения фактического расстояния уменьшается и длина очага деформации – особенно важная характери- стика процесса при определении условий вторичного захвата.

Поэтому при работе станов винтовой прокатки на повышенных углах подачи необходимо учитывать искажение очага деформации, вызванное углом подачи. Существует достаточно много работ по определению геометрических параметров очага деформации при прошивке [2–9], но существующие математические модели по геометрическим зависимостям очага деформации при точной постановке задачи приводят к сложным громоздким выражениям и уравнениям 4-го порядка, решение которых достигается различными итерационными способами, или водятся допущения, способствующие снижению точности расчета.

В результате создания CAD-программ, например, КОМПАС-3D и SolidWorks, основные геометрические зависимости в очаге деформации находятся при помощи твердотельного моделирования, основанного на поверхностном моделировании с граничным представлением твердых тел.

Данный подход является наиболее точным, но для его реализации необходимы навыки работы в CAD-программах.

Основная сложность в разрабатываемой математической модели связана с определением расстояния от оси прокатки до поверхности валков в любом поперечном сечении очага деформации. Для прошивных станов с бочковидными валками такая задача решена. При этом использовались следующие допущения: радиус-вектор кратчайшего расстояния rx направлен по прямой, перпендикулярной оси валка и проходящий через ось заготовки; изменение радиуса заготовки в основной меридиональной плоскости незначительное. Кратчайшее расстояние между осями заготовки и валка в любом сечении очага деформации [6] находится по выражению rx = B'-R',                                   (1)

где R ‘ и B ‘ - радиус валка в рассматриваемом поперечном сечении и расстояние между осями заготовки и валка в плоскости, перпендикулярной оси валка и отсекающей на оси прошивки отрезок, равный x .

B' = ^ ( R n + r )² + x ² • sin² в ,                (2)

где R_п – радиус валка в пережиме валка; r_п – радиус заготовки в пережиме валков.

Радиус R’ валка равен

R ‘ = R_n - x • cos ₽• tg a ь ,                      (3)

где в - угол подачи; a b - угол валка.

Приведенные зависимости применимы для станов с бочковидными валками. Для прошивных станов с грибовидными валками расстояние между осями заготовки и валка в плоскости, перпендикулярной оси валка определяется по выражениям: для конуса прошивки

B^r = л] ( R 0 + r₀ - x b • sin ф )² + x ² b • cos² ф^ sin² в ;   (4)

для конуса раскатки

B' = ( R 0 + r ₀ + x b • sin ф )² + x ² _b • cos² ф^ sin² в , (5)

где ф - угол раскатки; R 0 - кратчайшее расстояние от оси валка до заготовки в оси поворота; r ₀ – радиус заготовки в оси поворота; x_b – отрезок на оси валка, образованный осью поворота валка и плоскостью перпендикулярной оси валка.

Для определения настроечных параметров прошивного стана необходимо найти зависимость между длиной очага деформации и расстоянием от оси прокатки до поверхности валков r_x ( x od ) . Данная зависимость получена на основе проведения плоскости перпендикулярной оси заготовки, и пересекающей ось валка на расстоянии x_b от оси поворота (рис. 1).

Из расчетной схемы текущая длина очага деформации связана с отрезком xb по следующему выражению:

xod xb = cosв^cosф

.

Подставив выражения (6) в (4) и (5), получили зависимость расстояния между осями заготовки валка от длины очага деформации:

для конуса прошивки

B' =

\cos для конуса раскатки

B' = AI(R0+ ro + xod^^g^)2 + x2od • tg2p ,(8)

уcos

Радиус валка в текущем сечении поперечного разреза очага деформации определен при допущении: изменение радиуса валка в его основной меридиональной плоскости незначительное (рис. 2).

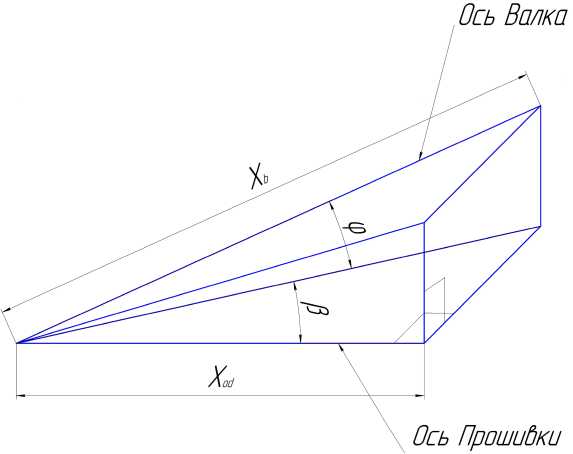
Рис. 1. Расчетная схема для определения длины очага деформации

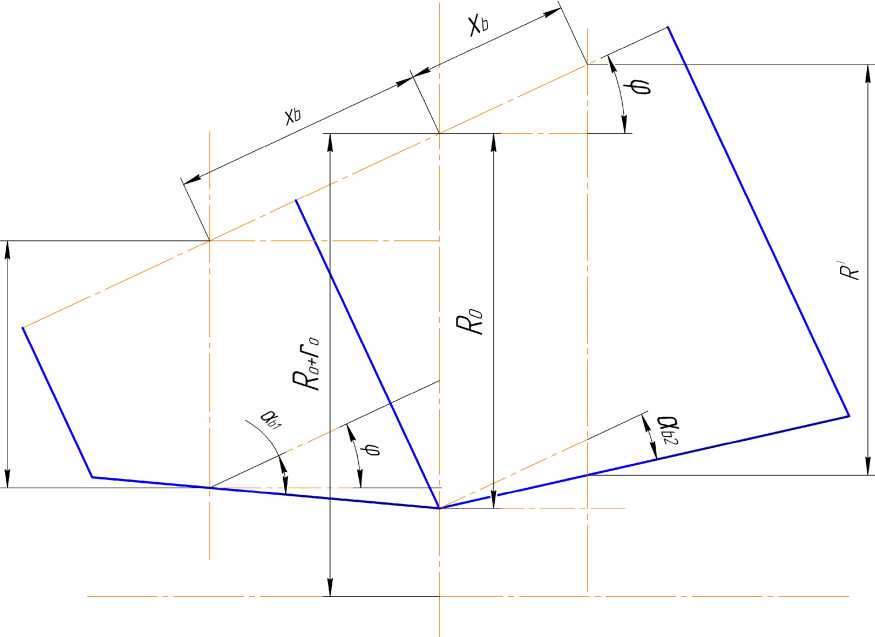
Рис. 2. Расчетная схема для определения радиуса валка в любом поперечном сечении

Радиус валка в конусе раскатки равен

R ' = R 0 + х ь - ( sin ф- cos ф- tg ( ф-а _b 2 ) ) ,    (9)

в конусе прошивки

R ‘ = R ^- x_b - ( sin ф + cos ф- tg ( а _{b 1} -ф ) ) . (10) где а ь1 - угол валка в конусе прошивки; а ь ₂ -угол валка в конусе раскатки.

В результате получены следующие зависимости между длиной очага деформации и расстоянием от оси прокатки до поверхности валков в любом поперечном сечении очага деформации:

для конуса прошивки

Гх (Xod ) = I(R0 + r - xod ' tg ф)2 + X2od ■ tg2p - cos р

^- R 0⁺---- Tod --( sin ф ⁺ cos ф- tg ( а b ! ^-ф ) ) ;    ⁽ 11)

cosр-cosф для конуса раскатки rx (xod ) = ЛI(R0 + r0 + od gф)2 + х2od " tg2P - R0 -cos в

-

----xod --( sin ф^- cos ф^- tg ( ф^-а b 2 ) ) . cos р- cos ф

Для оценки погрешности, обусловленной принятым допущением, в КОМПАС-3D было про- ведено твердотельное моделирование процесса прошивки на двухвалковом стане винтовой про- катки с грибовидными валками при различных углах подачи. Параметры моделирования: угол раскатки 15°; радиус валка в пережиме 650 мм; угол валка в конусе прошивки 18 град; угол валка в конусе раскатки 12°. На рис. 3 и 4 приведены изменения расстояния от оси прокатки до поверхности валков в основной меридиональной плоскости заготовки Ar, полученное в результате твердотельного моделирования и расчета по выражениям (11) и (12).

Сравнение значений rx (xod) показало хоро шую сходимость и правомочность принятого допущения. Наибольшее отклонение наблюдается в конусе прошивки при угле подачи 18°, на длине очага деформации xod = 500 мм и равно 6,9 %.

На основе полученных выражений разработана методика по определению основных настроечных параметров процесса винтовой прошивки (рис. 5): расстояние между валками в пережиме валков; выдвижение оправки за пережим валков; обжатие перед носком оправки, расстояние от захвата заготовки валками до носка оправки.

Радиус заготовки в оси поворота совпадает с половинным расстоянием между валками в их пережиме а/ 2 = r₀ .

Для правильного позиционирования оправки в очаге деформации необходимо найти длину очага

Конус прошивки

Конус раскатки

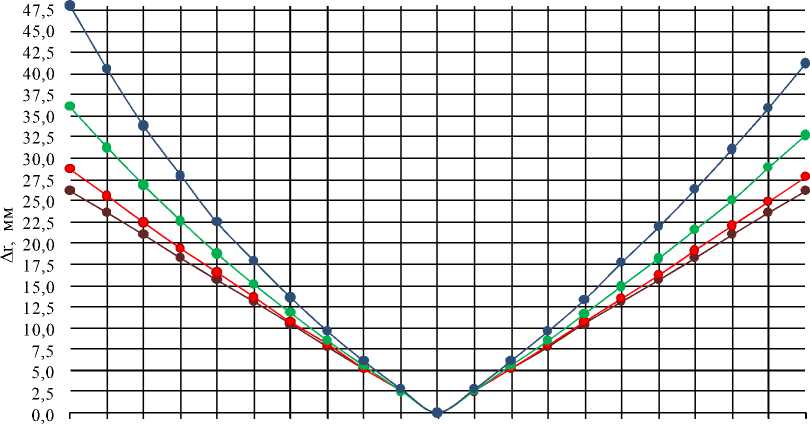
-500-450-400-350-300-250-200-150-100 -50 0 50 100 150 200 250 300 350 400 450 500

Длина очага деформации^, мм

Рис. 3. Изменение по длине очага деформации кратчайшего расстояния от оси прокатки до поверхности валков, полученное в результате моделирования

Конус прошивки              Конус раскатки

45,0 1 42,5 40,0 37,5 35,0 ( 32,5 30,0 g 27,5 ( 1 25,0 | < 22,5 20,0 17,5 15,0 12,5 10,0 7,5 5,0 2,5

> —•— р-о° —•— р=6° —•— Р=12° —•— Р=18°

и,и -500-450-400-350-300-250-200-150-100 -50 0 50 100 150 200 250 300 350 400 450 500 Длина очага деформации, мм

Рис. 4. Изменение по длине очага деформации кратчайшего расстояния от оси прокатки до поверхности валков, полученное в результате расчета

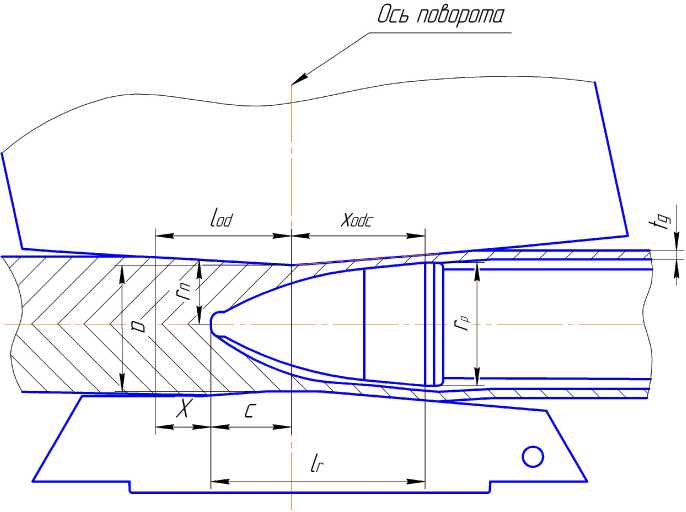
Рис. 5. Схема очага деформации при двухвалковой винтовой прошивке

деформации в конусе раскатки xodc , где формируется толщина стенки гильзы. Длина очага деформации определяется из выражения rp+tg=л(R+-0'+^dc^"^^          -

\           cos P

- R 0-- x odc --( sin ф — cos ф- tg ( ф —a b 2 ) ) ,   (13)

cos p- cosф ^{x                          7}

где r_p – радиус оправки; t_g – толщина стенки

гильзы.

Из выражения (13) длина очага деформации, где формируется стенка, равна

x odc

— B — V B ² — 4 - A - C 2 - A

где A , B , C – величины, вычисляемые по следую-

щим выражениям:

A =

( sin ф — cos ф- tg ( ф —а ь 2 ) ) 2

cos² P - cos² ф

— tg² p — -tg²^ ; (15) cos p

необходимо учитывать обжатие перед носком оправки 8 n и расстояние от захвата заготовки валками до носка оправки X , так как от этих величин зависят условия захвата и качество получаемых гильз.

Обжатие перед носком оправки равно

( г- п )

8_Я= -z— n - 100%,                    (19)

n I - z )

где r_z – радиус заготовки; r_n – радиус перед носком оправки, равный

• -n = «I ( R 0 ⁺ - o ^— c ¹^)^{2 +} c ^{2 -} tg² e ^{— R} 0 ⁺ cos p

• +----- c --( sin ф + cos ф- tg ( a _{b 1} — ф ) ) . (20)

cos p- cosф ^{x                          7}

Расстояние от захвата заготовки валками до носка оправки X определяется из выражения

X = l od — c ,                               (21)

n _ ^ (          Л ⁽ sin ф ^— cos ф ^- tg ⁽ф ^— “ b ² ) )

B 2 - (rP + tg + R0 ) -             о x            7         cosp-cosф

где l_od – длина очага деформации в конусе про-

шивки, полученная из следующего выражения

—

• —2-(R0 + ro)- дф ;(16)

cos p

C = (-p + tg + R0)2 —(ro + R0)2 .(17)

Определив длину очага деформации в конусе раскатки, рассчитывается выдвижение оправки за пережим валков по формуле

• c = lr — xodc ,

- z = ( R 0 + - 0 — ^lod -^ltg ^ )² + 1 ² od • tg² e — R 0 + cos P

+---- ^l- od- --( ^sin ф + ^cos ф^- tg ( a b 1 ^—ф ) ) .

cos p- cosф ^{x                          7}

В результате решения уравнения (22) очага деформации в конусе прошивки равна

= ^— B 1 ^— BB_X ^{— 4 - A} 1 ^{- C} 1 ^lod               2 - A 1             ,

длина

где l_r – длина оправки.

При определении настроечных параметров

где A ₁ , B ₁ , C ₁ – величины, вычисляемые по сле-

дующим выражениям:

A =

( sin ф + cos ф- tg ( a b 1 -ф ) ) 2 cos² P- cos² ф

- -tg£ - tg² p ; (24) cos² P

2-(R 0 +r)-tgф

Bi =-- cos P

2-(rz + Rо)'(sinФ + cosФ-tg(abi -ф)) cosP-cosф

C i = ( R^ + r z ) 2 - ( R ‘+ r₀ ) 2 .

Таким образом, получены математические за- висимости, которые позволяют определить расстояния от оси прокатки до поверхности валков в любом поперечном сечении очага деформации при двухвалковой винтовой прошивке. На основе полученных выражений разработана методика по определению основных настроечных параметров процесса винтовой прошивки: расстояние между валками в пережиме валков; выдвижение оправки за пережим валков; обжатие перед носком оправки, расстояние от захвата заготовки валками до носка оправки. Разработанные математические зависимости пригодны также для разработки калибровки прокатного инструмента прошивных станов: оправок, валков и для проведения анализа схем деформирования заготовок при винтовой прошивке.