Определение настройки расчётной точки инструмента для обеспечения точности обработки деталей на станках с ЧПУ

Существенной проблемой проектирования программ обработки деталей и эксплуатации станков с ЧПУ является точность деталей, обеспечивающая выход высокой вероятности принятой продукции, сохранения материальных ресурсов, энергии, труда и времени при производстве высокоточных деталей современного производства.

Преодолевая начальный этап обеспечения точности изготовления деталей на станках с ЧПУ, было принято приемлемое решение строить программу расчёта траекторий расчётных точек инструмен-тов1 для обработки поверхностей детали не по номинальной геометрии детали, а от середины поля допуска на геометрию наружных обводов детали.

Для дальнейшего совершенствования и повышения точности обработки потребовались уточнения представления о следующих проблемах:

• -    обеспечения адекватной оценки реальной геометрии детали,

• -    правил и методов оценки точности станочного оборудования (станков с ЧПУ, измерительных систем и т. п.), используемых для обработки и контроля геометрии деталей,

• -    правил и методов настройки расчётных точек инструментов для высокой вероятности приёмки продукции², соответствующей требованиям сборки с точки зрения собираемости и работоспособности изделия.

В данной статье сделана попытка подойти к решению последней проблемы.

Особенности формирования поверхностей деталей машиностроения при изготовлении на станках с ЧПУ

Поверхности деталей машиностроения формируются на заключительных (чистовых) переходах технологии обработки. Результат формирования параметра геометрического элемента детали (поверхности, линии сечения или сопряжения) в технологическом процессе механической обработки деталей на станках с ЧПУ получается за счёт настройки x Н расчетной точки инструмента, окончательно формирующего поверхности детали, на середину поля допуска формируемой поверхности.

Все множество геометрических параметров изделий машиностроения3 и видов полей допусков на их геометрические параметры можно условно разделить на две группы:

• –    параметры, номинальное значение которых x ном ≠ 0 может находиться на неограниченном интервале - ∞ <  x ном < + ∞ , а действительное значение параметра x на интервале, ограниченном границами поля допуска x min ≤ x ≤ x max (таких большинство);

• –    параметры, номинальное значение которых x ном = 0, а действительное значение параметра x на интервале, ограниченном границами поля допуска 0 ≤ x ≤ x max (таких много меньше).

Действительное значение геометрического параметра объекта производства (ОП) в технологическом процессе (ТП) изготовления детали является результатом взаимодействия технологии4, средств технологического обеспечения5 (СТО), формирующих геометрию детали с погрешностями геометрических параметров поверхностей и измерения сформированного параметра с погрешностью6 измерения. Использование оборудования с ЧПУ исключило из участников формирования геометрических параметров поверхностей детали человека-рабочего.

Значение геометрического параметра реального ОП и положение его значения относительно границ поля допуска имеет неопределенность, обусловленную случайным характером, как погрешности формирования параметра, так и погрешности его измерения.

Согласно К. Шеннону [1] мерой неопределенности ситуации, описываемой случайной величиной геометрического параметра x , является энтропия:

+∞

H = - ∫ p ( x )ln p ( x ) dx,

-∞ являющаяся функционалом дифференциальной функции распределения p(x) случайной величины x в партии изделий, производимых по одинаковой технологии одними и теми же СТО.

Количественной мерой энтропии является величина интервала , соответствующего заданной доверительной вероятности Р д экспериментально установленного закона распределения, полученного при обработке статистики результатов изготовления группы деталей при одних и тех же условиях (технологии, СТО).

Установление закона распределения геометрического параметра совокупности деталей представляет собой процедуру нахождения соответствия реального распределения известному закону распределения по так называемым критериям согласия⁷ [2], зависящему от числа случайных величин в группе. Изменение числа деталей приводит к разным законам распределения и, соответственно, к разным величинам интервалов доверительной вероятности Р д .

В реальной жизни ни один из известных законов распределения погрешностей формирования параметров и измерения не выполняется. Однако некоторая часть из них имеет большой практический интерес. Этот интерес сводится к следующему.

Допустим, что случайная величина изменяется на некотором ограниченном или неограниченном интервале по закону распределения, параметры которого экспериментально установлены. Каким должен быть закон с известными статистическими параметрами (например, размахом R x , математическим ожиданием µ x , и дисперсией D x ,), имеющий те же границы рассеяния, чтобы интервал, соответствующий доверительной вероятности Р д , был наибольшим из всех возможных?

Если такой закон использовать при оценках практических интервалов рассеяния реальных распределений, имеющих те же границы, что и у закона распределения, используемого вместо реально- го, полученного экспериментально, то интервал рассеяния реального закона при тех же значениях вероятности Рд будет находиться внутри практического интервала рассеяния модельного закона, используемого вместо реального.

Следовательно, при любых реальных законах распределения, имеющих те же границы изменения, модельное распределение, используемое вместо реального распределения, обеспечит наибольший интервал рассеяния, то есть обеспечит интервальную вероятностную «оценку сверху», то интервал распределения больше этого не будет. При тех же значениях выборки из генеральной совокупности доверительной вероятности Рд, интервал рассеяния реального закона распределения не выйдет за пределы практического интервала рассеяния модельного закона, используемого вместо реального закона распределения.

В ряде теорем теории информации [1] К. Шеннон доказал следующие фундаментальные утверждения:

• 1)    если энтропия непрерывного процесса со случайной координатой, принимающей значения только на отрезке [ a, b ] соответствующему размаху R случайных значений, то интервал, соответствующий заданной доверительной вероятности Р д максимален при равномерной (равновероятной) плотности распределения ;

• 2)    в случае, когда известна дисперсия D x случайной координаты непрерывного процесса, то интервал, соответствующий заданной доверительной вероятности Р д максимален при нормальном законе распределения с той же дисперсией ;

• 3)    для существенно положительных величин с заданным средним (математическим ожиданием Ц х ), интервал, соответствующий заданной доверительной вероятности Р д максимален при экспоненциальном законе распределения.

Отсюда следуют важные для практических расчетов рекомендации.

Если известно, что рассеяние параметра не выходит за пределы отрезка [ a, b ], то независимо от действительного характера его распределения на этом отрезке максимальная неопределенность и практический интервал рассеяния, соответствующий доверительной вероятности Р д будет наибольшим при равновероятном законе . Иными словами, если на этом интервале параметр распределен по любому закону, отличному от равновероятного, доверительные интервалы рассеяния его соответствующие вероятности Р д находятся внутри доверительного интервала равновероятного распределения.

В случае, когда известна дисперсия D x параметра, функция распределения вероятностей p ( x ) изменяется на неограниченном интервале ( x min < x <  x max ), доверительный интервал рассеяния его при той же доверительной вероятности Р д будет наибольшим, если параметр распределен по нормальному закону (Гаусса) с дисперсией D x . Интервалы рассеяния других распределений, имеющих то же значение D x , при той же вероятности Р д находятся внутри доверительного интервала нормального распределения .

Если параметр существенно положителен, функция распределения вероятностей p ( x ) изменяется на интервале (0< x <  + да ) или (0< x < x max ), то при одном и том же математическом ожидании ц х и доверительной вероятности Р д доверительный интервал на экспоненциальном законе будет охватывать аналогичные интервалы любых других распределений на неограниченном интервале.

Таким образом, первичные параметры статистической обработки данных: размах R , дисперсия D x и математическое ц x ожидание непосредственно связаны с видом закона распределения, обеспечивающим оценку «сверху» интервалов рассеяния, соответствующих заданной доверительной вероятности Р д .

Начнём с первой, более многочисленной группы геометрических параметров ОП, для которой границы поля допуска формируются на интервале ( x min <  x <  x max ).

Предположим, что при аттестации технологии и СТО, выбранных для формирования параметра ОП (например, длины стержня L), при неизменной настройке расчётной точки инструмента хн на ожидаемый результат и режимах процесса формирования параметра, произведено m объектов. Каждый j-й объект (j=1, 2, .., m) будем многократно измерять средством измерения. При обработке дан- ных измерений (i=1, 2, …, nj) каждого j-того объекта определим действительную величину Lj каждого j-того объекта измерений. После обработки результатов nj измерений Lj действительное значение Lj будет совпадать с математическим ожиданием центра группирования:

nj

L j = E L ,! n .

= 1

Для совокупности всех m объектов измерения L j определим математическое ожидание центра группирования µ Lj показаний L ij средства измерения:

m ц ц = E L , / m = х н j = 1

и выборочную дисперсию

m sLj 2 = E (Lj - MLj )2 ! m .

j = 1

Используя вторую теорему Шеннона, можно предположить, что «оценкой сверху» закона распределения погрешности формирования параметра L при изготовлении будет нормальное распределение относительно центра группирования µ Lj с выборочной дисперсией s Lj ².

В дальнейших рассуждениях центр группирования µ Lj будем отождествлять с настройкой рабочей точки инструмента х Н при формировании геометрического параметра в технологическом процессе, используемом для группы одноимённых объектов производства.

Уравнение функции нормального закона распределения (рис. 1 а ) имеет вид:

(x-xH )2 - p 1(x, xh) = e  2^x  / ст, 2П,, где: xН – положение настройки расчетной точки инструмента при формировании параметра, σx – параметр распределения формирования параметра в технологическом процессе константы: число π и е – основание натуральных логарифмов.

Настройку удобнее представлять координатой x , соответствующей математическому ожиданию для деталей, выполненных по одному и тому же технологическому процессу одними и теми же СТО при одних и тех же режимах, а распределение относительно математического ожидания в координатах p ( x ) – функция и σ x , – аргумент, представляющий долю координаты x (рис. 1, а ).

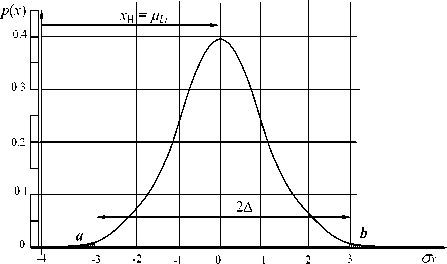
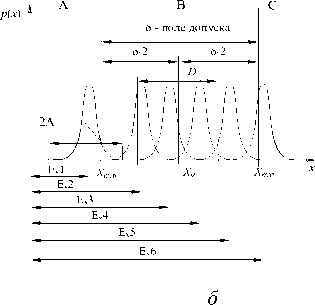
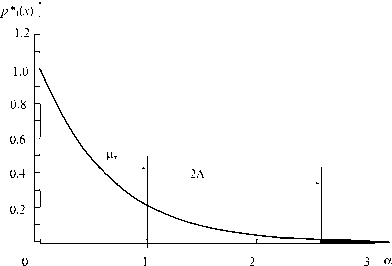
Рис. 1. Распределение формирования параметра ОП: а – на неограниченном интервале, б – положение практического интервала рассеяния 2 Δ и поля допуска δ

Интервал 2 Δ охватывает площадь под кривой распределения погрешности формирования параметра p ( x ) с доверительной вероятностью Р д = 0,9973, что соответствует принятой за норму в технологии машиностроения стандартному практическому интервалу .

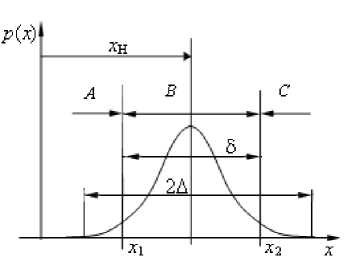
Понятие точности формирования геометрического параметра для отдельно взятой группы ОП при формировании этого параметра в ТП с применением конкретных СТО связанно со степенью соответствия поля рассеяния полю допуска этого параметра в конструкторской документации.

В самом общем случае (рис. 1, б ) границы поля допуска делят весь интервал значений параметра x на 3 области А, В и С, которым соответствуют годные ОП, исправимый и неисправимый брак. Распределение наименований областей (годные, исправимый и неисправимый брак) зависит от свойств самих ОП.

При формировании параметров необходимо, чтобы практический интервал распределения погрешности формирования геометрического параметра ( x min , x max ), был заключен в некотором наперед заданном интервале ( X min , X max ):

( X min , X max ) ⊆ ( x min , x max ).

Для того, чтобы отношение (1) могло быть выполнено, необходимо, чтобы интервал погрешности 2 Δ параметра детали был меньше или равен полю допуска 2 δ на параметр ОП:

2 Δ ≤ δ . (2)

Однако, условие (2) не является достаточным. При его выполнении возможны различные варианты расположения практического интервала распределения операционной погрешности относительно поля допуска.

Пусть погрешность формируемого параметра подчиняется нормальному закону с настройкой Е х , соответствующей математическому ожиданию и погрешностью формирования, определяемой средним квадратическим отклонением 6 σ х = 2 Δ ≤ δ .

В вариантах настройки математических ожиданий E x 1 и E x 6 процесса формирования параметра условие (2) не выполняется и неизбежно получение ОП, бракуемых по параметру x , относительное количество (вероятность) которых определяется площадью областей, выходящих за пределы поля допуска.

Для того чтобы та или иная операция технологического процесса (ОТП) обеспечивала заданную точность необходимо и достаточно, чтобы нижняя граница поля допуска X min была меньше нижней границы рассеяния параметра ОП или равна ей, а верхняя граница поля допуска была больше верхней границы рассеяния параметра ОП или равна ей:

X min ≤ x min ,

X max

≥ x max .

Соответствие границ доверительного интервала поля рассеяния параметра c заданной вероятностью появления его внутри этих границ, заданному полю допуска и его расположению называют точностью формирования параметра в ТП (точностью изготовления).

Точность технологического процесса зависит от закона распределения суммарной погрешности формирования геометрического параметра в технологической операции, настроенности (положения центра группирования) в технологическом процессе на формирование величины геометрического параметра и положения поля допуска.

Для сопоставления поля рассеяния с полем допуска применяют коэффициенты точности [ 3]

Δ

3 σ x

K δ ^.

К Т = η = δ

Для определения смещения уровня настройки технологического процесса используют коэффициент настроенности процесса К Н :

Е x - X 0

К Н =    _δ

.

Точность и настроенность технологического процесса считаются достаточными, если поле рассеяния параметра в технологическом процессе не превосходит заданного поля допуска.

Величина интервала, в пределах которого возможно изменение настройки процесса относительно середины поля допуска, соответствует соотношению

D <  2 А - 5 .

Тогда настройка формирования параметра E x находится внутри интервала:

X o - D /2 <  E x <  X o + D /2.

В этом случае доля брака не превзойдет 0,27 %. Если хотя бы одна из границ поля рассеяния выхолит за пределы поля допуска, то доля брака увеличивается выше допустимого значения, равного 0,27 %.

В случае идеальной точности и настроенности процесса при А = 5 получаем п = 1 и D = 0.

Если п >  1, то в таком случае можно говорить о коэффициенте запаса точности . Если D >  0, то в таком случае по аналогии с предыдущим можно говорить о запасе настраиваемости.

Точные и неточные процессы при завершающем этапе формирования геометрии поверхности детали (чистовой обработке) и настройке расчётной точки инструмента на середину поля допуска представлены на рис. 2.

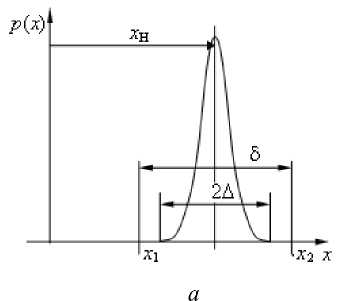
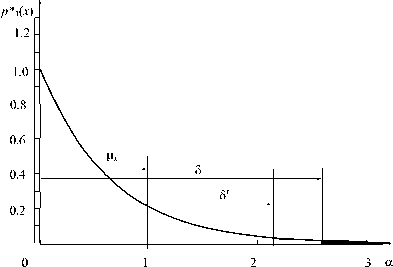
Рис. 2. Погрешность формирования параметра ОП и поле допуска: а – стандартный интервал рассеяния формируемого геометрического параметра ОП 2 Δ = 6 σ , намного меньше интервала поля допуска (x1, x2), б – стандартный интервал рассеяния формируемого геометрического параметра ОП 2 Δ = 6 σ , больше интервала поля допуска (x1, x2)

Если при достаточно высокой доверительной вероятности (например, 0,9973) интервал рассеяния параметра при его формировании существенно меньше интервала поля допуска, чему соответствуют п >  1 и D >  0, такие процессы формирования параметров считают точными по отношению к формируемому параметру. Но это бывает далеко не всегда.

Если же интервал рассеяния параметра при его формировании равен или больше интервала поля допуска, то такие процессы формирования параметров считают неточными . В последнем случае п <  1, D < 0. Это бывает в практической деятельности взаимодействия конструкторских, технологических и производственных подразделений предприятий гораздо чаще.

Кроме этих двух крайних случаев возможны и промежуточные, когда стандартный интервал рассеяния параметра объекта производства, равный 6 о , вблизи границ интервала поля допуска ( X min , x max ).

В точных технологических процессах настройка расчётной точки инструмента для параметров, номинальное значение которых x ном ^ 0 и находится на неограниченном интервале - да <  x ном < + да , может быть осуществлена на середину поля допуска.

Для параметров, номинальное значение которых x ном = 0, а действительное значение параметра x на интервале, ограниченном границами поля допуска 0 <  x <  x max настройка осуществляется на номинальное значение x ном = 0.

В неточных технологических процессах всё выглядит гораздо сложнее.

Края интервала рассеяния действительных значений геометрического параметра в неточных технологических процессах выходят за границы интервала поля допуска.

Если поля допусков деталей обеспечивают собираемость и работоспособность соединяемых поверхностей деталей при и после сборки, часть ОП, имеющих геометрические параметры, соответствующие заданным полям допусков, будут приняты для сборки с другими деталями. Детали с геометрическими параметрами не соответствующими полям допусков не будут приняты. Их признают браком неисправимым или исправимым. Поэтому неотъемлемой составляющей процесса оценки формирования геометрических параметров детали в процессе производства является технический контроль.

В процессе формирования параметров ОП их все подряд или периодически измеряют. Главной целью измерений является определение принадлежности действительного значения параметра продукции границам и интервалам полей допусков, представленных в конструкторской документации. Все ОП после завершения формирования их параметров на том или ином этапе технологического процесса подвергают приемке.

Если все параметры ОП соответствуют границам и интервалам полей допусков, представленных в конструкторской документации, то ОП считают принятыми (годными для передачи на последующие этапы производства или эксплуатации в соответствии с назначением) с вероятностью Р п . ОП, в которых хотя бы один параметр не соответствует требованиям конструкторской документации, считают браком с вероятностью Р б .

Погрешности средств измерений (измерительных приборов) оказывают влияние на результат разделения ОП по действительному значению измеряемого параметра к годным (принятым) или браку. В составе годных могут оказаться ошибочно принятые объекты, измеряемый параметр которых не соответствует наложенным ограничениям. Относительное количество таких объектов в составе принятых называют вероятностью риска заказчика Р рз . С другой стороны, в составе брака могут быть ошибочно забракованные объекты. Относительное количество таких объектов, в составе забракованных, называют вероятностью риска производства Р р_П .

Встала проблема не допустить в составе принятых по данному геометрическому параметру изделий, не соответствующих полю допуска.

Представители заказчика (военпреды) придумали как.

Поле допуска имеет конечную величину. Погрешность измерения также. Если поле допуска уменьшить с двух сторон на величину погрешности измерения, то получим приёмочное поле допуска. Уменьшение вероятности попадания ОП в состав соответствующих полю допуска может быть обеспечено введением приемочных границ x ^Т min , x ^Т max , компенсирующих погрешности измерений параметра в неточном ТП.

Хорошо? Хорошо-то хорошо, да ничего хорошего. Приёмочное поле допуска меньше конструкторского (ничем не обоснованного) поля допуска. А за продукцию отвечает не конструктор, а директор завода. Для него важен выход годной (принятой) продукции. Брак нежелателен и не допустим. Во многих отечественных производствах число использованных заготовок существенно превосходит число принятой продукции.

Однако при больших интервалах погрешностей измерения это приводит к существенному уменьшению части поля приёмочного поля допуска вплоть до отрицательных чисел и возрастанию вероятности брака Р б .

Следствием такого приема является существенное возрастание вероятности признания ОП браком, что приводит к дополнительным затратам по его исправлению (регулировке) в случае исправимого брака с вероятностью Р иб или к дополнительным потерям затраченных ресурсов (материалов, энергии, времени, труда) от неизбежных потерь, связанных с утилизацией неисправимого брака пропорционально вероятности Р нб .

Для точных ТП введение приемочных границ допуска компенсирует погрешности средств измерений и влияет только на частоту измерений ОП (выборок) для корректировки (подналадки) настройки x н в ТП при его осуществлении [4].

Приемочные границы и настройка положения центра группирования влияют на вероятность риска заказчика, относительный объем (вероятность) исправимого и неисправимого брака Р иб и Р нб .

Если известны:

• -    погрешность формирования геометрического параметра, соответствующая технологии и СТО, используемым при изготовлении детали,

• -    погрешность однократного измерения геометрического параметра используемым средством измерения,

то возможно определение величины коррекции расчётной точки инструмента относительно середины поля допуска, обеспечивающей допустимые вероятности неисправимого брака Р нб и уменьшения риска заказчика Р рз .

Измерение параметра множества однородных измеряемых объектов отградуированным средством измерения при одной границе поля до-пуска

Определение действительной величины каждого значения геометрического параметра ОП связано с многократными измерениями каждого объекта и затратами времени на завершение формирования продукции, соответствующей требованиям конструкторской документации. Это существенно увеличивает важнейшую характеристику современного производства –цикл производства и снижает производительность. Поэтому в технологическом процессе практически все измерения физических параметров объектов производства выполняют однократно . Для оценки закона вероятности погрешности однократных измерений измерительными приборами разработаны специальные методы и средства [5].

Решение первой проблемы оценки погрешности однократного измерения свелось к разработке программного обеспечения (ПО) для определения и сохранения в памяти программируемого контроллера, границ пучка функций преобразования измерительного прибора (рис. 3, а ) и вычисления погрешности однократного измерения (рис. 3, б ).

Верхняя граница y Реакция системы измерения

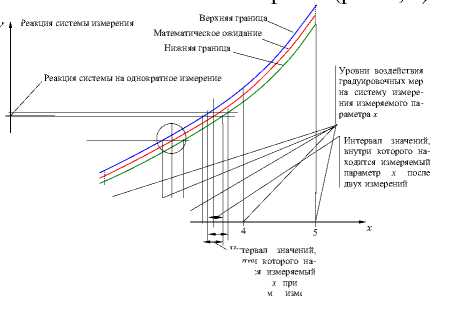
Математическое ожидание

Нижняя граница

Уровни воздействия градуировочных мер на систему измерения измеряемого параметра x

Реакция системы на однократное измерение

Интервал значений, внутри которого находится измеряемый параметр x после двух измерений

x

Интервал значений, внутри которого находится измеряемый параметр x при однократном измере- xmin 3 xm

а

y

ерхняя граница

p ( x )

p ( y )

x

Сигнал средства измерения ижняя граница

б

Рис. 3. К погрешности однократного измерения измерительным прибором: а – построение границ градуировочных характеристик, б – распределение вероятности погрешности измерения

В соответствии с первой теоремой К. Шеннона погрешность однократного измерения распределена по равновероятному закону между точками пересечения сигналом канала измерения верхней и нижней границ пучка градуировочных характеристик измерительного прибора (рис. 3, а и б ).

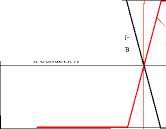
Рассмотрим приемку продукции по одному параметру при однократном его измерении отградуированным средством измерения. Она сводится к определению вероятности принадлежности результата измерения к области допустимых значений параметра. Назовем эту границу x 1 конструкторским допуском . Вес интервал значений x значение конструкторского допуска x 1 делит на две части А и В (рис. 4, а ) .

Если область действительных значений измеряемого параметра находится достаточно далеко от границы x 1 (например, слева или справа рис. 4, а ), то при однократном измерении параметра x принадлежность действительного значения измеряемого параметра по показанию измерительного прибора не вызывает сомнений о принадлежности его областям А и В.

Когда область действительных значений измеряемого параметра пересекается с границей х 1 слева, то часть распределения погрешности измеряемого параметра может оказаться за границей х 1 и вероятность принадлежности к области А будет меньше (площадь заштрихованной области распределения погрешности измерения).

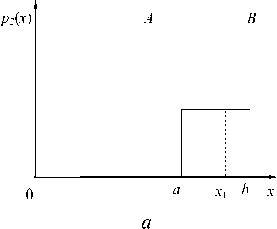
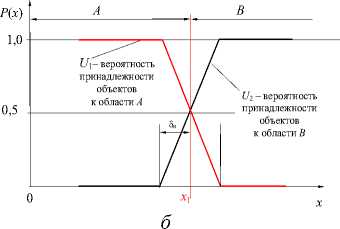
Рис. 4. Вероятность принадлежности параметра объекта измерения различным областям при погрешности измерения, определяемой равновероятным законом распределения: а – оценка вероятности принадлежности показания средства измерения областям А и В, б – характер зависимости принадлежности

Чем больше пересечение области действительного значения измеряемого параметра с границей х 1 , тем меньше вероятность принадлежности действительных значений параметра х к области А.

По мере удаления от границы х 1 вероятность Р ( х ) совпадения результата оценки действительного значения параметра объекта производства по измеренному при однократном измерении отградуированным средством измерения возрастает и в пределе стремится к 1.

При погрешности измерения ±8 и (рис. 4 б) , подчиняющейся равновероятному закону, характерному для погрешности однократного измерения отградуированным средством измерения⁸, вероятность принадлежности объектов области А , по результатам однократных измерений соответствует зависимости U 1 .

На интервале 0 < х < ( х 1 - А /2) U 1 = 1.

На интервале ( х 1 - А /2) < х < ( х 1 + А /2) U 1 =( х 1 -х )/ А +1/2.

На интервале ( х 1 + А /2) < х < да U 1 = 0.

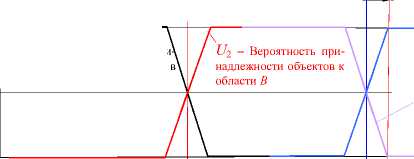
Для объектов, принадлежащих области В , по результатам однократных измерений вероятность оценки их принадлежности этой области соответствует зависимости U 2 .

На интервале 0 < х < ( х 1 - А /2) U 2 = 0.

На интервале ( х 1 - А /2) < х < ( х 1 + А /2) U 2 =( х-х 1 )/ А +1/2.

На интервале ( х 1 + А /2) < х <да U 2 = 1.

В каждой точке действительных значений измеряемого параметра х U 1 + U 2 =1.

Объекты, действительно принадлежащие области А будут ошибочно признаны принадлежащими области В (часть зависимости U 2 внизу слева от х 1 на рис. 4 б ).

Объекты, действительно принадлежащие области В будут ошибочно признанны принадлежащими области А (часть зависимости U 1 внизу справа от х 1 на рис. 4 б).

Измерение геометрического параметра множества однородных измеряемых объектов отградуированным средством измерения при двух границах конструкторского поля допуска

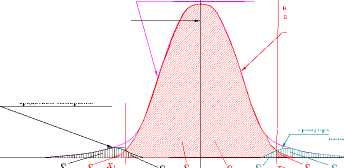
Введем на оси значений параметра х вторую границу конструкторского допуска х2. Получим поле допуска между двумя границами х 1 и х2. Весь интервал значений х разделится на три части А, где: да < х < х 1; В, где: х 1 < х < х2 и С, где: х2 < х < + да. Будем считать, что по измеряемому параметру об- ласть А соответствует неисправимому браку, область В - годным объектам, область С - исправимому браку (рис. 5).

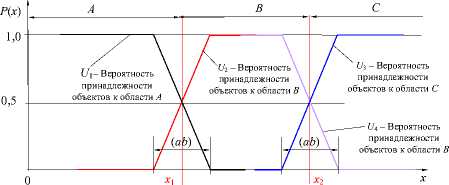
Р ( x )

P ( x )

1,0

0,5

Брак

U ] - Вероятность принадлежности объектов к области А

U 2 - Вероятность принадлежности объектов к области В

Годные изделия

Брак

\   / U3 - Вероятность при надлежности объектов к

\ / области С

/\  /U4 - Вероятность при надлежности объектов к области В

x

• 2.    Распределение параметра объекта производства при однократном определении принадлежности к области В отградуированным средством измерения

x Н = ( x 1 , x 2 )/2

Распределение параметра объекта производства при его формировании в технолог песком процессе

I. Распределение параметра объекта производства при однократном определении принадлежности к области А отградуированным средством измерения ____

’ 6

' 7

' 5

' 1

• 3.    Распределение параметра объекта производства при однократном определении принадлежности к области С отградуированным средством измерения

x

а                                                  б

Рис. 5. К влиянию погрешности измерения на принадлежность параметра объекта измерения различным областям при двух границах поля допуска: а – погрешность измерения, определяемой равновероятным законом распределения на двух границах поля допуска; б – искажение средством измерения результатов оценки принадлежности объектов производства к областям А, В и С по измеряемому параметру при настройке расчётной точки инструмента на середину поля допуска

При измерении средством измерения с равновероятным характером распределения погрешности получим картину вероятности принадлежности к каждой из трех областей. Для объектов, принадлежащих областям А, В и С по результатам однократных измерений вероятность оценки их принадлежности этой области соответствует зависимостям U i , U 2 , U 3 и U 4 .

На интервале 0 <  x <  ( x 1 - А /2) U 1 = 1.

На интервале ( x 1 - А /2) <  x < ( x 1 + А /2) U 1 = ( x 1 - x )/ А + %.

На интервале ( x 1 + А /2) <  x < да U 1 = 0.

На интервале 0 <  x <  ( x 1 - А /2) U 2 = 0.

На интервале ( x 1 - А /2) <  x < ( x 1 + А /2) U 2 = ( x - x 1 )/ А + %.

На интервале ( x 1 + А /2) <  x <  ( x 2 - А /2) U 2 = 1.

На интервале ( x 1 + А /2) <  x <  ( x 2 - А /2) U 4 = 1.

На интервале ( x 2 - А /2) <  x < ( x 2 + А /2) U 4 = ( x 2 - x )/ А + %.

На интервале ( x 2 + А /2) <  x < да U 4 = 0.

На интервале 0 <  x <  ( x 2 - А /2) U 3 = 0.

На интервале ( x 2 - А /2) <  x < ( x 2 + А /2) U 3 = ( x - x 1 )/ А + %.

На интервале ( x 2 + А /2) <  x <  да U з = 1.

Для области А U 1 + U 2 = 1, для области В U 1 + U 2 = 1 и U 1 + U з = 1, для области С U 2 + U з = 1.

По мере удаления от границы x 1 в область А вероятность Р ( x ) совпадения результата оценки измеренного значения параметра объекта производства при однократном измерении аналоговым средством измерения и действительного его значения возрастает и в пределе стремится к 1.

Количественные оценки интересующих нас принадлежностей одноимённых геометрических параметров однородных объектов к каждой области можно представить, как анализом формул, так и наглядным представлением графиками функций.

Часть объектов, действительно принадлежащих области А будет ошибочно признана принадлежащей области В (часть зависимости U 2 внизу слева от x 1 на рисунке). С ругой стороны, часть объектов, действительно принадлежащих области В будет ошибочно признана принадлежащей области А (часть зависимости U 1 внизу справа от x 1 на рисунке .

Часть объектов, действительно принадлежащих области В будет ошибочно признана принадлежащей области С (часть зависимости U 3 внизу слева от x 2 на рисунке .

Часть объектов, действительно принадлежащих области С будет ошибочно признана принадлежащей области В (часть зависимости U 2 внизу справа от x 2 на рисунке .

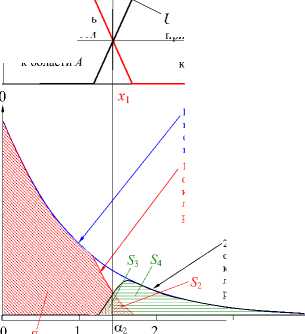
Рассмотрим случай, когда центр группирования x Н рассеяния (настройки) параметра ОП в неточном ТП настроен на середину поля допуска.

Предположим, что области А и С соответствуют браку, область В – объектам, годным по измеряемому параметру.

Рассмотрим определение количества принятых и забракованных ОП, принадлежащих областям А , В и С, симметричных относительно середины области В (рис. 5, б ) .

Задача определения количества объектов, принадлежащих областям А , В и С, симметрична относительно середины области В. Определим результаты приемки по правой части рисунке, удваивая полученный результат. Из симметрии следует, что S 1 = S 5 , S 2 = S 6 , S 3 = S 7 , S 4 = S 8 .

x ₂

S 1 =

∫ p 1 ( x Н , σ ф ) ⋅ U 4 ( x 2 ) ⋅ dx ;

xН

+∞

S 2 = ∫ p 1 ( x Н , σ ф ) U 4 ( x 2 ) ⋅ dx ;

x ₂

x ₂

S 3 = ∫ p 1 ( x Н , σ ф ) ⋅ U 3 ( x 2 ) ⋅ dx ;

xН

S 4 =

+∞

∫ p 1 ( x Н , σ ф ) U 3 ( x 2 ) x ₂

⋅ dx.

В составе принятых объектов будут объекты, пропорциональные площади S 2 и S 6 , фактически принадлежащие областям А и С. Они представляют собой вероятность риска заказчика .

Среди объектов, отнесенных по контролируемому параметру к областям А и С (браку), объекты, пропорциональные площадям S 3 и S 7 , представляют собой вероятность риска производства поскольку будут отнесены к браку.

Окончательные результаты сортировки могут быть представлены следующими соотношениями:

– вероятность принятых ОП ( Р г) пропорциональна 2( S 1 + S 2 );

– вероятность забракованных ОП ( Р б) пропорциональна 2( S 3 + S 4 );

• –    вероятность риска заказчика ( m ) пропорциональна 2 S 2 ;

• –    вероятность риска производства ( n ) пропорциональна 2 S 3 .

В большинстве практических случаев области А и С не равноправны. Одна из них, например, А может быть областью неисправимого брака, другая ( С ) – областью исправимого брака.

Из проведенного качественного анализа стратегии поведения для достижения уменьшения вероятностей объема неисправимого брака и риска заказчика в случае, когда стандартный интервал рассеяния параметра объекта производства, равный 6 σ , больше интервала поля допуска ( x 1 , x 2 ) следует:

• –    со стороны области неисправимо брака необходимо смещать настройку центра группирования погрешности формирования параметра в сторону годной продукции;

• –    со стороны области исправимого брака – вводить приемочный допуск также в сторону годной продукции;

• –    для увеличения выхода годной продукции после приемки с первого предъявления необходимо исправление исправимого брака с последующей приемкой исправленных объектов.

Для удовлетворения ограничениям, налагаемым на технологический процесс, необходимо с одной стороны уменьшить потери от неисправимого брака ( вероятность неисправимого брака Р НБ ) до приемлемого допустимого уровня [ Р НБ ], с другой – обеспечить качество продукции, доведя приемлемой величины в составе принятой продукции допустимую вероятность риска заказчика [ m ].

Первую задачу, как показали предшествующие исследования, можно решить сместив настройку x Н в сторону области В, одновременно уменьшая вероятность оценки принадлежности объектов к ней и вероятности риска заказчика при однократных измерениях средствами контроля .

Вторую задачу можно решить, вводя границу приемочного поля допуска x Т , смещая ее в сторону области В, и уменьшая тем самым вероятность риска заказчика m в составе объектов , принятых с первого предъявления по контролируемому параметру до начала исправления исправимого брака (рис. 6) .

C

p ( x )

A                     B

Неисправимый брак

Годные изделия

P ( x )

1,0

0,5

U1– Вероятность при надлежности объектов к области А

Исправимый брак

U ₄ – Вероятность принадлежности объектов к области В

U ₃ – Вероятность принадлежности объектов к области С

Распределение параметра объекта

формирова- производства при его нии в технологическом процессе xН= (x1, x2)/2

x ′ Н

1. Распределение параметра объекта производства при однократном определении принадлежности к области А отградуированным средством измерения

2. Распределение параметра объекта производства при однократном определении принадлежности к области В отградуированным средством измерения

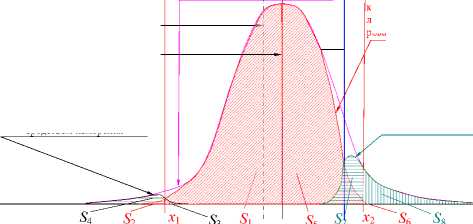
x

3. Распределение параметра объекта производства при однократном определении принадлежности к области С отградуированным средством измерения

Рис. 6. Искажение средством измерения результатов оценки принадлежности объектов производства к областям А, В и С при смещении настройки xН в сторону исправимого брака и введении приемочной границы поля допуска в сторону области В от второй границы поля допуска

Вероятность общего количества объектов, принятых с первого предъявления по однократно измеряемому параметру объектов, принадлежащих по результатам однократных измерений области В , будет равна S В = ( S 1 + S 2 + S 5 + S 6 ).

Вероятность неисправимого брака на границе между областями А и В равна площади (S3+S4), где x1

S 3 =

∫ p 1 ( х ′ Н , σ ф ) ⋅ U 1 ( x 1 ) ⋅ dx,

-∞

+∞

S 4 =

∫ p 1 ( х ′ Н , σ ф ) ⋅ U 1 ( x 1 ) ⋅ dx.

x ₁

Величину смещения настройки в новую точку х ′ Н можно определить из условия:

( S 3 + S 4 ) = [ Р Б ].

После подстановок получим уравнение:

x ₁

∫ p ( х ′ Н , σ ф ) ⋅ U 1 ( x 1 ) ⋅ dx +

-∞

+∞

∫ p 1 ( х ′ Н , σ ф ) ⋅ U 1 ( x 1 ) ⋅ dx = [ Р Б ],

x ₁

решив которое относительно х ′ Н определим положение настройки для обеспечения наименьших потерь времени, труда и затрат за счет уменьшения неисправимого брака.

Теперь можно перейти к определению вероятности первой части принятых ОП с левой стороны рисунка Она равна сумме площадей ( S 1 и S 2 ), где:

S 1 =

x ₁

∫ p ( х ′ Н , σ ф ) U 2 ( x 1 ) ⋅ dx ;

-∞

S 2 =

x ′ _Н

∫ p ( х ′ Н , σ ф ) U 2 ( x 1 ) ⋅ dx.

x ₁

Вероятность риска заказчика m 1 в левой части рисунка равна площади S 2 .

m 1 =

x ₁

∫ p ( х ′ Н , σ ф ) U 2 ( x 1 ) ⋅ dx.

-∞

Вторая часть принятых ОП связана с правой частью рисунка. Для этой части важно обеспечить заданный риск заказчика [ m ] = m 1 + m 2 , где m 2 зависит от положения границы приемочного допуска x ^Т 2 . Эта приёмочная граница служит для уменьшения вероятности суммарного риска заказчика при первой приёмке с первого предъявления.

В соответствии с рисунком вероятность риска заказчика m 2 будет равна площади S 6 , которая определяется по формуле:

m 2 = S 6 =

+∞

∫ p 1 ( x ′ Н , σ ф ) ⋅ U 4 ( x ^Т 2 ) ⋅ dx .

Т x2

Решая последнее уравнение относительно x ^Т 2 , получим значение положения границы приемочного поля допуска со стороны исправимого брака.

Вероятность второй части принятых ОП с правой стороны рисунка равна сумме площадей ( S 5 и S 6 ), где

S 5 =

+∞

∫ p 1 ( x ′ Н , σ ф ) ⋅ U 4 ( x ^Т 2 ) ⋅ dx. x ′ _Н

В составе принятых объектов будут объекты S 2 и S 6 , фактически принадлежащие областям А и С. Объекты, равные площади ( S 2 + S 6 ) представляют собой вероятность риска заказчика m . По сравнению с предыдущим рисунком сумма площадей, S 2 и S 6 , определяющих вероятность риска заказчика, будут существенно меньше.

Объекты, отнесенные по контролируемому параметру к области А , характеризующие вероятность неисправимого брака, пропорциональные площади S А = S 3 + S 4 , также будут меньше. Среди них будут объекты равные площади S 4 , принадлежащие фактически области В , являющиеся частью вероятности риска производства n .

Объекты, отнесенные по контролируемому параметру к области С (исправимому браку), равны площади S С = S 7 + S 8 , где:

T x 2

S 7 =

J p i ( х н , О ф ) - U з ( x Т2 ) • dx ;

x ′ _Н

+∞

S 8 = J p 1 ( х Н , О ф ) - U з ( x Т2 ) • dx.                                   (16)

Т x 2

Этих объектов будет существенно больше, чем на предыдущем рисунке. Среди них будут объекты равные площади S 7 , принадлежащие фактически области В. Объекты, равные сумме площадей S 4 + S 7 представляют собой вероятность риска производства n .

Для уменьшения риска производства следует проконтролировать все изделия, соответствующие площади S с = S 4 + S 7 и исправить в них отклонения от поля допуска.

Перейдём ко второй группе ОП, параметры номинальных значений которых x ном = 0, а действительное значение параметра x на интервале, ограниченном границами поля допуска 0 <  x <  x max (таких много меньше).

Если при аттестации технологии и СТО для формирования параметра ОП (например, отклонения от перпендикулярности x = а ) при неизменной настройке его на ожидаемый результат х н = 0 и режимах процесса формирования параметра, произведено m объектов. Из-за случайных флуктуаций условий выполнения процесса формирования параметра а j (j’ = 1, 2, 3, .., m ) все объекты от первого до m -го будут иметь разную величину.

Каждый j-й объект будем многократно измерять средством измерения. При обработке данных n измерений (i = 1, 2, ., nj) каждого j-того  ^ aji / nj.

i = 1

Будем считать, что действительная величина а j каждого объекта измерений будет отличаться от нуля. С размерами а j каждого объекта поступим следующим образом: определим математическое ожидание центра группирования всех результатов измерений:

m

Р а = ^ o j / m = а н .

j = 1

По одной из теорем теории информации К. Шеннона, «оценкой сверху» закона распределения погрешности формирования параметра существенно положительных величин, для которых функция распределения вероятностей p ( x ) изменяется на интервале (0 <  x < + да ), при одном и том же математическом ожидании Ц х = р а и вероятности P д интервал экспоненциального закона будет охватывать аналогичные интервалы любых других распределений на том же интервале (0 <  x < + да ).

Уравнение функции экспоненциального закона распределения имеет вид:

• - λ x

p 1 ( x ) = л е , где X = 1/ р x = Up a j .

В отличие от предыдущего случая, характерного для нормального распределения не придётся менять масштаба для определения математического ожидания и параметра, служащего для отсчёта аргумента x. Всё можно определять в одном масштабе математического ожидания. Вид этого закона при X = 1 представлен на рис. 7, а .

а                                                   б

Рис. 7. Распределение формирования параметра ОП на интервале, ограниченном только положительными значениями: а – интервал 2 Δ охватывает площадь под кривой распределения p(x) с доверительной вероятностью Рд = 0,9973, что соответствует 2,5686 µ x и принятой за норму в технологии машиностроения стандартному практическому интервалу, б – интервал δ соответствует полю допуска на существенно положительный геометрический параметр, а интервал δ Т приёмочному полю допуска, обеспечивающему уменьшение риска заказчика

Настройка расчётной точки инструмента, формирующего геометрический параметр геометрического элемента, производится на границу приёмочного поля допуска.

Всю область значений параметра α поле допуска делит на 2 части: А , соответствующую интервалу поля допуска 0 ≤ α ≤ α 2 для принятых (годных) ОП, и В , соответствующую интервалу α 2 ≤α <  ∞ , для отбракованных ОП.

Объекты, принадлежащие области А – годные и могут быть принятыми. Объекты, принадлежащие области В – брак.

При контроле значений параметра ОП отградуированным средством измерения с целью определения принадлежности к области А исходный характер распределения будет искажаться погрешностью измерения в соответствии с вероятностью оценки принадлежности к области А (рис. 8 а ).

1,0

^{P ( α )}    A–годные

B– брак

Распределение параметра объекта производства при однократном определении принадлежности к области А отградуированным средством измерения

x

Распределение существенно положительного параметра объекта производства при изготовлении

0,5

p ( α )

U ₁ – вероятность принадлежности объектов к области А

Распределение параметра

U2 – вероятность принадлежности объектов к области В объекта производства при однократном определении принадлежности к области В отградуированным средством измерения

α

P ( α ) 1,0

0,5

p ( α )

A–годные

B– брак

U ₁ – вероятност принадлежност объектов к области А

0            x _Т1

U ₂ – вероятность

принадлежност и

объектов к области В

Распределение существенно положительного параметра объекта производства при изготовлении

Распределение параметра

объекта производства при однократном определении принадлежности к области А отградуированным средством измерения

S 3   S 4

S 2

0 _S       1   α ^Т1 ^α 1      2

2 – Распределение параметра объекта производства при однократном определении принадлежности к области В отградуированным средством измерения

α

а                                                   б

Рис. 8. Искажение средством измерения результатов оценки принадлежности объектов производства к областям А и В по измеряемому параметру при настройке инструмента на x = 0: а – распределение принадлежности при контроле по конструкторскому допуску, б – распределение принадлежности при контроле по приёмочному допуску

При контроле значений параметра объекта производства исходный характер распределения будет искажаться погрешностью измерения в соответствии с вероятностью оценки принадлежности к области А. Каждое значение параметра распределения формирования параметра объекта производ- ства p(α) следует умножить на вероятность P(α) определения принадлежности к соответствующей области А или В:

p^* 1 ′ ( x ) = p^* 1 ( λ , α ) ⋅ U 1 ( α 1 ),

p^* 2 ′ ( x ) = p^* 1 ( λ , α ) ⋅ U 2 ( α 1 ),

- λα где p 1(λ, α) = λe    – распределение погрешности формирования параметра в технологическом процессе;

α Н – настройка формируемого параметра в технологическом процессе α Н = 0;

λ = 1/ µα = 1/ µ α j – параметр распределения экспоненциального закона распределения формируемого параметра;

p^* 1 ′ ( α ) и p^* 2 ′ ( α ) – соответственно искаженные средствами контроля распределения объектов, принадлежащих по результатам приемочного контроля областям А и В .

Вероятность принадлежности объектов к областям А и В по результатам однократных измерений средством измерений можно оценить по площади под искаженной кривой вероятности распределе--λα ния параметра р 1(λ, α) = λe   .

Объекты, пропорциональные площади S A = S 1 + S 2 по результатам однократных измерений отградуированным средством измерения по параметру x должны быть признаны соответствующими области A ( вероятности признанных годными Р г ) а объекты, пропорциональные площади S В = S 3 + S 4 , должны быть признаны соответствующими области В ( вероятности неисправимого брака P нб ).

S A + S B =( S 1 + S 2 )+( S 3 + S 4 )=1.

Здесь:

S 1 =

x ₁

∫ p^* 1 ′ ( α ) ⋅ dx=

x ₁

∫ р^* 1 ( λ , α ) ⋅ U 1 ( α 1 ) ⋅ dx ,

-∞

-∞

S 2 =

+∞          +∞

∫ p^* 2 ′ ( α ) ⋅ dx= ∫ p^* 1 ( λ , α ) ⋅ U 1 ( α 1 ) ⋅ dx ,

x ₁

x ₁

S 3 =

x ₁

∫ p^* 1 ′ ( α ) ⋅ dx=

x ₁

∫ p^* 1 ( λ , α ) ⋅ U 2 ( α 1 ) ⋅ dx ,

-∞

-∞

S 4 =

+∞

∫ p^* 2 ′ ( α ) ⋅ dx=

+∞

∫ p^* 1 ( λ , α ) ⋅ U 2 ( α 1 )

⋅ dx.

Площадь S А под кривой 1 соответствующая объектам, принадлежащим по результатам измерений к области А равна сумме площадей S 1 и S 2 .

Если площадь S А соответствует годным объектам, то из объектов, признанных принадлежащими области А, вероятность объектов, фактически принадлежащих области А , будет равна площади S 1 :

S 1 =

x ₁

∫ p^* 2 ′ ( x ) ⋅ dx=

x ₁

∫ p^* 1 ( λ , α ) ⋅ U 1 ( α 1 ) ⋅ dx.

-∞

-∞

Вероятность объектов принадлежащих фактически области В и ошибочно признанных принадлежащим области А будет равно площади S 2 – вероятность риска заказчика m :

m = S 2 =

+∞

∫ p^* 2 ′ ( x ) ⋅ dx=

+∞

∫ p^* 1 ( λ , α ) ⋅ U 1 ( α 1 )

⋅ dx.

x ₁                      x ₁

Если площадь S В под кривой 2, равная сумме площадей S 3 + S 4 соответствует негодным (забракованным) объектам, то из объектов, признанных принадлежащими области В, то вероятность ошибочно забракованных, фактически принадлежащие области А, будет равно площади S 3 – так называемая вероятность риска производства n :

n = S 3 =

x ₁

∫ p^* 2 ′ ( x ) ⋅ dx=

x ₁

∫ p^* 1 ( λ , α ) ⋅ U 2 ( α 1 ) ⋅ dx.

-∞

-∞

Из представленного на рис. 6 соотношения площадей (вероятностей), близких к реальности следует, что риск производства S 3 всегда больше риска заказчика S 1 поскольку p(x Н , σ ф ) на участке слева от x 1 всегда больше, чем справа, а характер изменения U 1 ( x 1 ) и U 2 ( x 1 ) вблизи x 1 одинаков.

Как изменить величину вероятности риска заказчика при условии приемки с первого предъявления ?

Для параметра, формируемого на неограниченном интервале риск заказчика можно уменьшить либо введением приемочного допуска в сторону области А от границы, либо смещением настройки в сторону области А от границы поля конструкторского допуска. Первый вариант уменьшения риска заказчика в данном случае приемлем, а второй нецелесообразен, поскольку непредсказуемо влияет на параметры закона распределения погрешности формирования геометрического параметра ОП (рис. 8 б ).

Как и при контроле по конструкторскому допуску х 1 , площадь S А под кривой 1 соответствующая объектам, принадлежащим по результатам измерений к области А равна сумме площадей S 1 и S 2 .

Вероятность приемки с первого предъявления объектов при однократном измерении отградуированным средством измерения равное площади S А будет меньше, чем в предыдущем примере. Если область А соответствует годным объектам, то из объектов, признанных принадлежащими области А вероятность объектов, принадлежащих фактически области А будет равно площади S 1 . Вероятность объектов, принадлежащих фактически области В , ошибочно признанных принадлежащим области А , будет равна площади S 2 , которая существенно меньше, чем в предыдущем примере. Вероятность объектов, принадлежащих области В в составе принятых – вероятность риска заказчика m . При приемке продукции по приемочному допуску вероятность риска заказчика уменьшается.

Площадь S В под кривой 2 соответствует объектам, принадлежащим по результатам измерений к области В равна сумме площадей S 3 и S 4 . Вероятность объектов, принадлежащих области В будет существенно больше, чем в предыдущем примере. Эта площадь соответствует вероятности риска производства n. Она будет больше, чем в предыдущем случае.

Следовательно, при приемке продукции по приемочному допуску вероятность риска производства увеличивается.

В случае приемки продукции по приемочному допуску с уменьшением вероятности риска заказчика m увеличивается вероятность брака Р б . Следует отметить, что в случае с существенно положительными величинами брак всегда исправим, и при последующем его исправлении вольется в состав годных объектов производства.

Рассмотрим точные технологические процессы, при которых область рассеивания параметра целиком и полностью находится в пределах области допуска (рис. 9).

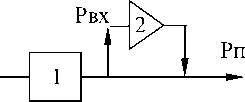
Рис. 9. КТП для точных ТП. 1 – последний технологический переход;

2 – выборочный контроль средством измерения

В таком случае все входные детали ( Р вх = 1) будут принятыми (годными): Р п .

Для неточных технологических процессов возникает ситуация, при которой возможно исправление брака исправимого после прохождения всей партией детали технического контроля.

Рассмотрим два случая: без исправления и при исправлении брака исправимого (рис. 10 а и б ):

Р вх

а                                                 б

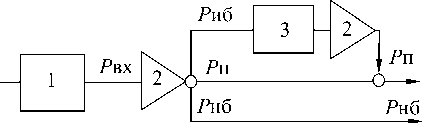
Рис. 10. КТП для неточных ТП. а– КТП без исправления брака; б – КТП с исправлением исправимого брака за один переход. 1 – последний технологический переход; 2 – контроль средством измерения; 3 – дополнительный технологический переход исправления брака исправимого

В случае, когда нет исправления брака исправимого (рис. 10, а ), все детали с вероятностью Р вх = 1, признанные годными, принимаются с вероятностью Р п . А весь брак, как исправимый, так и неисправимый, списывается как брак с вероятностью Р б .

В случае, когда исправимый брак весь исправляется за один переход (рис. 10, б ), итоговый брак значительно меньше Р нб < Р б .

Сравнительная оценка необходимости смещения расчетной точки программным компонентом.

Разработанный программный компонент статистического вероятностного анализа использует помимо вероятностных оценок более качественные – численные оценки количества используемых деталей для обеспечения каждого из возможных видов КТП характерной оценки целесообразности. Такими оценками являются:

– К вх – коэффициент умножения числа ОП на входе в КТП по отношению к числу принятых ОП на его выходе,

– К п – относительное количество принятых ОП, приведенное к количеству принятых ОП на выходе,

– К б =1/Р б – относительное количество забракованных ОП, приведенное к количеству принятых ОП на выходе

– К и = 1/Р и – относительное количество ОП, подвергаемых исправлению брака, приведенное к количеству принятых ОП на выходе.

Результативной оценкой является сравнительная характеристика выходных данных для последующего решения: осуществлять или нет дополнительный переход исправления брака исправимого.

Для реального производства при оценке необходимости исправления брака исправимого применяется разработанный нами программный компонент. Используя минимальный набор входных данных, можно оценить следующие вопросы:

– Является ли процесс точным или нет?

– Какова вероятностная оценка качества применения вышеуказанных технологических процессов и есть ли необходимость применять исправление исправимого брака?

– Проводить ли анализ, как в случае определения положения инструмента на центр поля допуска, так и со смещением расчетной точки в сторону от этого значения?

– Какова относительная оценка приведенного количества деталей (параметров) в партии для принятых, отбракованных и исправленных объектов?

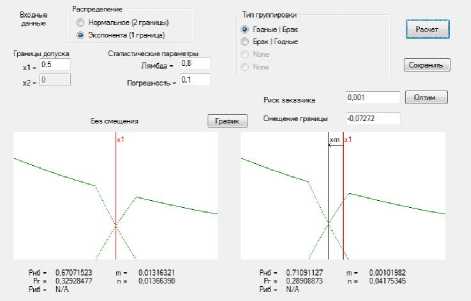
Входными данными являются: конструкторские границы поля допуска, статистический параметр нормального распределения σ и погрешность отградуированного контрольно-измерительного устройства. Так же следует указать расположения областей годности относительно границ поля допуска, выбрав один из предложенных вариантов (рис. 11).

Распределение водные данные ф1 Нормальное (2 границы)

О Экспонента (1 граница)

Границы допуска          Статистические параметры х1= 0                      Сигма=   0

х2 = ®                      Погрешность =

Тип группировки                             __________

ё Неисправимый I Годные I Исправимый ^ Расчет

■ Исправимый I Годные I Неисправимый

1 _ • Годные I Исправимый I Неисправимый

¹ Неисправимый I Исправимый I Годные | Сохранить

Распределение

Входные данные '_) Нормальное (2 границы)

(ф Экспонента (1 граница)

Границы допуска          Статистические пара метры

Х1 = 0                         Лямбда = О х2= °______I              Погрешность = °

Тип группировки

•ё Годные! Брак

1 _ ■ Брак I Годные

1.1 None

| Сохранить |

а

б

Рис. 11. Интерфейс программы «Входные данные»: а – для геометрических параметров x min ≤ x ≤ x max ; б – для геометрических параметров 0 ≤ x ≤ x max

Программный компонент обладает следующими функциями: определение необходимого оптимального смещения расчетной точки инструмента относительно середины поля допуска, основной расчет всех имеющихся параметров, включая оценки КТП для всех трех основных типов техпроцессов и построение графиков, сохранение выбранного значения смещения в отдельный файл для прямого доступа операционной системой обрабатывающего станка.

Для определения оптимального размера смещения расчетной точки работает алгоритм пошагового сравнения показателя вероятности образования случайной величины на границе с неисправимым браком и смещением центра распределения случайной величины за одну итерацию цикла. Результатом будет являться число, которое после и сохраняется в отдельный файл. Используя два вида расчета: с настройкой на центр поля допуска и со смещением относительно этой настройки, можно проследить 6 возможных вариантов обработки и выбрать наиболее подходящий для применения.

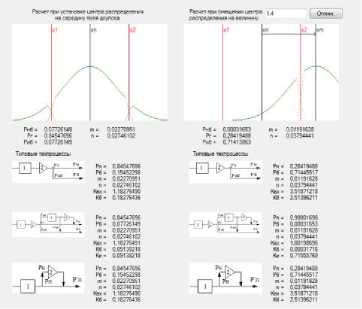
а

Рис. 12. Интерфейс программы. Выходные данные для двух типов расчетов: а – для геометрических параметров x min ≤ x ≤ x max ; б – для геометрических параметров 0 ≤ x ≤ x max

б

Данный программный компонент позволяет проводить статистический анализ применения смещения и подбора типа КТП для конкретных условий буквально за секунды. Скорость расчета не превышает 1.5 секунд при стандартной производительности компьютеров. Низкий объем входных данных так же упрощает процесс применения программного компонента и затраты трудоемкости на использование его в процессе производства.

В составе программного компонента используются стандартные утилиты средств разработки Visual Studio , в т.ч. Windows Forms , являющийся графическим модулятором для создания приложений, обеспечивающих интерфейс приложения, основанный на среде Microsoft Windo ws, начиная с версии Windows XP SP1 .

В состав программного компонента входят следующие элементы:

• 1    – Графическая оболочка Form ;

• 2    – 5 полей для ввода информации TextBox ;

• 3    – Группа из 4 флажков выбора RadioButton ;

• 4    – 3 функциональных кнопки Button ;

• 5    – 107 полей вывода текстовой информации Label ;

• 6    – 8 полей для вывода графической информации PictureBox , два из которых с подключенным компонентом построения графики Graphics ;

• 7    – Компонент вывода информации в отдельный файл SaveBox , используемый воссозданным методом SaveToFile ;

• 8    – Библиотека алгебраических функций cmath .

Программа содержит 3 используемых функций и один метод. Общий код программы (включая графическую настройку атрибутов компонентов и необходимые комментарии) 2 728 строк. В ходе работы подключается до 18 переменных одновременно, из которых только 14 переменных типа double (объем одной переменной типа double составляет 8 байт).

Выполнение операций происходит потоковым образом, используя условные функции, ситуации выбора и циклы. Максимальная глубина цикла (ситуация при которой цикл или условная функция находится внутри другого тела цикла или условной функции) – 5. Число операций не превышает 1 000 000 ед/сек за одну итерацию вложенного цикла. Общее число операций одной функции не превышает 500 000 000 ед/сек. При выполнении программы на устройствах с тактовой частотой процессора 2.5 ГГц, чистое время операции (без учета нагрузки на память) не превысит 2 сек. Программа пригодна для любого современного компьютера, время обработки данных составит не более 2 сек, общая нагрузка на аппаратуру, в сравнении со стандартным программным обеспечением, будет незначительна.

Заключение

В представляемой работе была поставлена цель – разработать специальный программный инструмент для оценки рисков появления брака и оптимизации технологического процесса с целью устранения неисправимого брака.

В ходе выполнения работы был разработан программный инструмент на языке программирования C ++, включающий в себя:

• 1.    Статистический анализ вероятностных оценок появления годной продукции, брака исправимого и неисправимого.

• 2.    Функцию определения смещения расчетной точки относительно центра поля допуска для полного или максимально возможного устранения неисправимого брака.

• 3.    Сравнительную характеристику показателей 6 типов комплексов конечных технологических переходов, по три для двух вариантов расположения расчетной точки;

• 4.    Доступный визуально-графический интерфейс программы на основе компонента Windows Form, обеспечивающий оптимальную работу на любом современном оборудовании при поддержке ОС Windows.

Данная программа способна быстро проводить анализ для любого типа геометрического параметра.