Определение несущей способности дважды коаксиальных пружин сжатия

Расчет коаксильных пружин сжатия не приводится в современной литературе, кроме известных классических методов расчёта пружин сжатия, работающих на деформацию кручения. Однопружинные конструкции были рассмотрены в работах авторов [1, 2] и предложены для реализации в работе [3]. Двухпружинные конструкции были рассмотрены в работах [4-6]. В настоящей работе дается теоретический расчёт конструкции, состоящей из трёх пружин сжатия (рис. 1).

Рассматриваемые пружины могут быть односторонней (правой или левой) или разносторонней завивки, что существенно влияет на распределение деформаций в пружинах и определение в них внутренних силовых факторов в зависимости от направления крутящего момента. Углом наклона винтовой линии к горизонтальной плоскости будем пренебрегать. При таком подходе каждые три смежных сечения при рассечении их вертикальной плоскостью будут находиться на одинаковом деформированном положении (рис. 2). В сечениях пружин возникают внутренние крутящие моменты – равнодействующие которых обозначены через T н – в сечении проволоки наружной пружины, T с – в сечении проволоки средней пружины и T в –в сечении проволоки внутренней пружины.

Принятые обозначения: F – приложенная внешняя сила; F н , F с , F в – составляющие силы F в наружной, средней и внутренней пружинах; R н. – наружный радиус пружинного вала, пружины; r н , r с , r в – средний радиус наружной, средней и внутренней винтовых линий проволок пружин; ℓ – высота цилиндрической части пружин; ι н , ι с , ι в – шаг винтовой линии проволок

Мартьянов Андрей Анатольевич, заведующий лабораториями кафедры «Сопротивление материалов»

наружной, средней и внутренней пружины; Е н , Е с , Е в – модули упругости первого рода наружной, средней и внутренней пружины; T н , T с , T в – равнодействующие внутренних крутящих моментов или сил в наружной , средней и во внутренней пружинах; A н =E н J ни , A с =E с J си , A в =E в J ви – изгибные жесткости наружной, средней и внутренней площади поперечных сечений проволок пружин; G н , G с , G в – модули сдвига проволок наружной, средней и внутренней пружины; J н , J с , J в – полярные моменты инерции при кручении; r нп , r сп , r вп – радиусы проволоки винтовых линий наружной пружины; d λ н , d λ с , d λ в – элементарные осадки пружин.

Для определения усилий в каждой пружине возьмем сумму проекций всех сил в пружинах на направление центральной оси Z. Из этой суммы следует

F = F н + F c + F в . (1)

Задача оказывается дважды статически неопределимой. Для раскрытия статической неопределимости воспользуемся принципом совместности деформаций трех смежных витков [4, 6]. Из рис. 2 видно, что при уменьшении или укорочении на текущей длине λ каждое второе смежное сечение получает приращение dλ. При совместной работе эти приращения будут одинаковыми, т.е. dλн=dλс=dλв или rнTнdsн / GнJн = rсTсdsс / GсJс= rвTвdsв / GвJв;   (2)

После интегрирования этого уравнения получим rнTнsн / GнJн = rсTсsс / GсJс = rвTвsв / GвJв.

Величину крутящего момента в каждой пружине определяем как произведение этой силы в этой пружине на соответствующий радиус винтовой линии. С учетом принятых обозначений из уравнения (3) следует

F н = F в r² в s в G н J н / r² н s н G в J в ,

F с = F в r² в s в G с J с / r² с s с G в J в ;        (4)

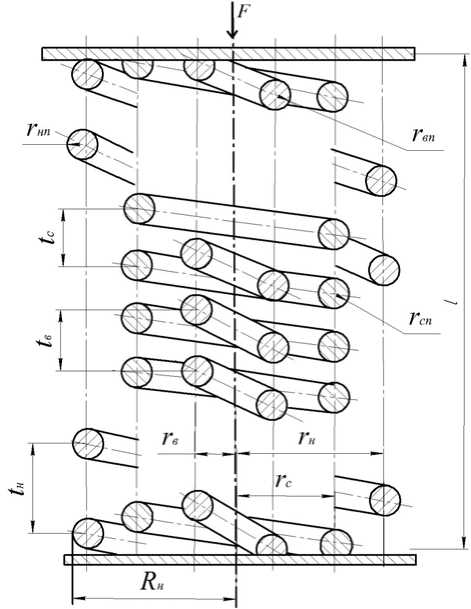
Рис. 1. Расчетная схема вала, состоящего из трёх завитых пружин, совместно работающих на кручение

средней и большой длины, что требует расчета на устойчивость при кручении проволок пружин. Основываемся на предположениях, что под действием крутящего момента Т происходит искривление проволоки пружины и пружина находится во втором состоянии равновесия. С учетом этого уравнения Кирхгофа-Клебша для одной – любой (индексы пружин опускаем и делаем выводы в общем виде) пружины приведут к виду [1]:

Ad ² u

J

Ad ² v

I dS

Tdv —---+ dS

5 F i

;

Tdu

—--+ OF\ dS 2

Здесь u и v – перемещения по осям x и y [4], А = ЕJ – изгибная жесткость проволок пружин. Величинами δF₁ и δF₂ пренебрегаем из-за их малости. Решением будет:

u — C cos aS + C sin aS + C

J ^{1                 2}                 3         (9)

v — - C 1 sin aS + C 2 cos aS + C 4

где С 1 , С 2 , С 3 , С 4 – постоянные интегрирования.

X — T/A ,          (io)

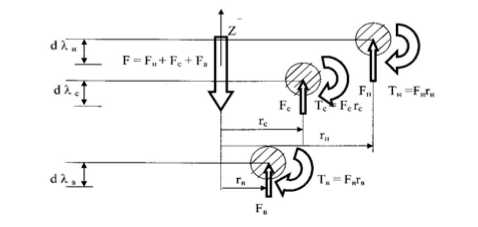
Рис. 2. Отсеченные вертикальной плоскостью три смежных витка пружины с внутренними крутящими моментами

Принимая условия закрепления концевых сечений для пружин по типу шарнирных опор, граничные условия можно записать в двух вариантах [6]:

• 1)    u — v — 0... при ... S — 0,... S — 2лт

• 2)    w — V v ² + u ² — 0... при ... S — 0,... S — 2nrn

  
  

где n – количество витков пружины, r – радиус винтовой линии пружины. Оба варианта приведут к равенству

Подставляя это соотношение в уравнение (1), найдем

F в = F/а,                         (5)

где а=1+ r _вs_вG_нJ_н / r _нs_нG_вJ_в + r _в s_в G_сJ_с / r _с s_с G в J в .

Равнодействующие внутренних сил в наружной и средней пружине будут равны:

F н = F(r² в s в G н J н / r² н s н G в J в ) / а,

F c = F(r² в s в G с J с / r² с s с G в J в ) / а;           (6)

Далее легко находятся внутренние крутящие моменты в проволоках пружин. Расчет на прочность при кручении каждой пружины общеизвестен. В данных же задачах гибкость проволоки пружин будет соответствовать стержням sin XS — 0.           (12)

Беря наименьший положительный корень равенства, получим

X S — n m,

где m – целое положительное число.

При m=1 критические значения крутящего момента с длиной проволоки выразятся одной за- висимостью вида:

T — 2n A /S сr

.

Здесь введены два значения критических пара- метров вместо одного параметра критической длины, что является равносильным. Применительно к наружной и внутренней пружинам бу- дем иметь:

T HCr = ^{2 n} E Н J НИ / S Н ,

T _CCr = 2 n E c J СИ I S C ,      (15)

T

ВСr

= 2 n E b J ВИ I S В

По зависимостям (5) и (6) определим следующие критические значения крутящих моментов в наружной, внутренней и средней пружинах:

T =Г r T = F r T = F r

НСr       СrН Н      ВСr      СrВ В ССr      СrС С

,, и соответствующие значения критических сил:

F _ ²™-^EB^J ВИ . F _ ^ ЯН ⁽ r H s H G B J B ) E H ^J НИ .

^ ^{cr e}" T b Sb ’ cr ^H"           bS н Г н           ’

F _ 2na(Гн sHGBJ В ) EcJ СИ crc "          bScrc

2                                  (17)

где b=r² в s в G н J н .

По зависимостям (17) можно сделать за- ключение, какая из трех пружин потеряет несущую способность первой или и с каким запасом работают две другие пружины. После потери устойчивости или несущей способности одной из пружин теряется несущая способность всей конструкции, если полную нагрузку не примут на себя другие пружины.

Выводы:

• 1.    Потеря устойчивости цилиндрических пружин сжатия и кручения происходит по разветвленным формам равновесия, у которых при больших гибкостях критические напряжения значительно меньше допускаемых.

• 2.    Значения критических сил и моментов определяют безотказную область работы пружин, за пределами которой теряется работоспособность за счёт быстрого (почти мгновенного) роста деформаций.

• 3.    Из полученных зависимостей для критических крутящих моментов и сил легко получаются их значения для одной пружины. В частных случаях из них вытекают формулы Греенхилла и Л.Эйлера.

• 4.    Валы сплошного круглого поперечного сечения с успехом можно заменить пружинными валами (Патент РФ № 37002 от 10.10.2004), что приводит к замене деформации кручения на деформацию растяжения или сжатия и к уменьшению энергетических затрат при работе данной конструкции.