Определение объектов на изображениях с помощью гистограммы направленных градиентов и метода опорных векторов

Гистограмма направленных градиентов (HOG) используется достаточно распространена в сфере компьютерного зрения. Метод был впервые предложен в 2005 году для обнаружения пешеходов в статических изображениях. В последующем он был расширен для обнаружения людей на видео, также как и для обнаружения различных животных и объектов. В данной статье будет рассмотрен принцип работы этого метода, а также метода опорных векторов для классификации пешеходов.

Дескриптор функции

Дескриптор функции — это представление изображения или части изображения, которое упрощает его, отбрасывая постороннюю информацию.

Как правило, дескриптор функции преобразует изображение размером ширина x высота x 3 (каналы) в вектор/массив длинны n. В случае дескриптора функции HOG входное изображение имеет размер 64 х 128 х 3 а вектор соответственно имеет длину 3780.

Нужно иметь ввиду, что дескриптор HOG можно рассчитать для других размеров, но в данной статье будут использованы размеры, описанные в оригинальной статье, описывающей данный метод.

В дескрипторе функции HOG в качестве функции используется распределение (гистограмма) направлений градиентов (ориентированных градиентов). Идея заключается в том, что величина градиентов велика вокруг краев и углов объектов (областей с резким изменением интенсивности).

Для расчёта дескриптора HOG нужны следующие шаги:

• 1.    Расчёт градиента . Вычисляется величину g_x и g_y градиента из оригинального изображения. Это можно сделать фильтрацией этого изображения со следующими ядрами:

  

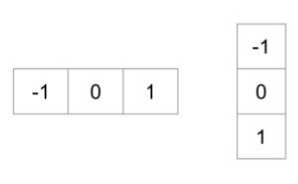
• 2.    Блоки. Изображение разделяется на блоки 8x8.

• 3.    Расчёт гистограммы градиентов в блоках. Для каждого пикселя в блоке 8х8 известен градиент (его величина и направление). Таким образом имеется 64 значения величины и 64 направления – 128 чисел. Гистограмма этих градиентов обеспечивает более полезное и компактное представление. Градиенты преобразуются в девяти интервальную гистограмму. Интервал гистограммы соответствует направлению градиента в 0, 20, 40 … 160 градусов. Каждый пиксель распределяет значение градиента в один или два интервала, основываясь на принадлежности угла градиента к тому или иному интервалу.

• 4.    Нормализация блоков. Гистограмма, рассчитанная в предыдущем шаге не очень устойчива к изменению освещения. Чтобы побороться с данным эффектом гистограмма нормализуется. Каждое элемент вектора гистограммы делится на величину вектора. В оригинальном описании метода HOG нормализация выполняется над блоками размером 16х16. Идея точно такая же, но вместо вектора длинны в 9 элементов получается вектор в 36 элементов.

• 5.    Характеристический вектор. Для подсчета конечного вектора из исходного изображения блок 16x16 двигается с шагом 8 и 36 значений, вычисленных на каждом шаге, конкатенируются в конечный вектор. Таким образом, с учетом размера входного изображения 64x128 пикселей, производится 7 шагов по горизонтали и 15 шагов по вертикали. Соответственно длина конечного вектора равна 105 х 36 = 3780.

Используя gx и gy вычисляется величина и направление градиента:

9=^$ + $

6 = arctail —

9x

Алгоритм обучения для классификации

На предыдущем этапе был разобран метод преобразования изображения в характеристический вектор. Теперь рассмотрим классифицирующий алгоритм, использующий характеристический вектор.

Перед стабильной работой, классифицирующий алгоритм нужно натренировать, показывая тысячи изображений на которых есть интересующий нас предмет и на которых его нет. Каждый алгоритм обучения учится по-разному, но главный принцип заключается в том, что они рассматривают характеристические векторы как точки в пространстве большей размерности и пытаются найти плоскости/поверхности, которые разбивают это пространство таким образом, что все объекты, принадлежащие, а одному классу, находятся на одной стороне плоскости/поверхности.

Для примера рассмотрим алгоритм под названием Метод опорных векторов (SVM).

SVM один из наиболее популярных алгоритмов двоичной классификации. Для удобства возьмём характеристический вектор размерностью 2.

Точки на изображении представляют два класса (присутствие объекта и его отсутствие). На изображении, расположенном ниже, два класса представлены двумя типами точек. В процессе тренировки алгоритму предоставляется много примеров изображений двух классов. Другими словами, алгоритм собирает информацию о координатах точек, а также, являются точки черными или белыми.

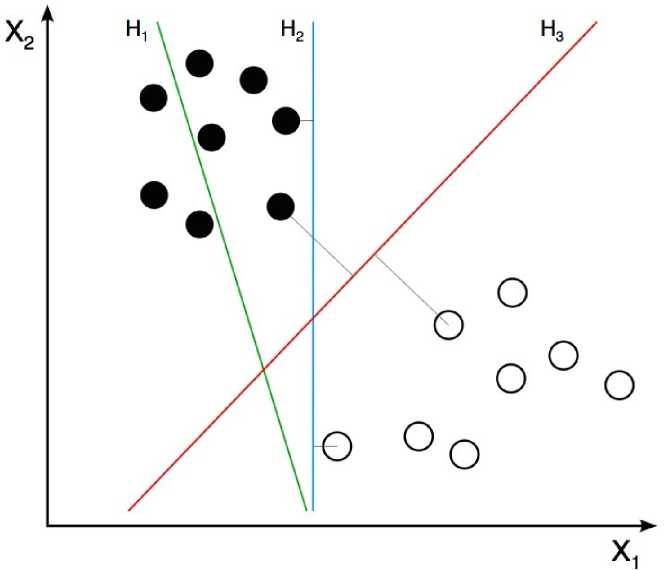
SVM пытается найти наиболее подходящую линию, которая разделяет два класса. На рисунке есть три линии H1, H2 и H3. H1 не разделяет два класса и не является хорошим классификатором. H2 и H3 разделяют два класса, но H3 делает это лучшим образом. Таким образом, в процессе тренировки SVM найдет линию H3.

Если вектор является трехмерным, SVM построит соответствующую плоскость, которая максимально разделяет два класса. Для дескриптора HOG будет построена гиперплоскость.

Реализация HOG в библиотеке OpenCV

В библиотеке OpenCV есть реализация метода HOG, а также натренированный по умолчанию SVM алгоритм для распознавания пешеходов.

Метод определения пешеходов на языке Python:

• #    инициализируем HOG дескриптор

hog = cv2.HOGDescriptor()

hog.setSVMDetector(cv2.HOGDescriptor_getDefaultPeopleDetector())

• #    папка с изображениями

imagePaths = sorted(paths.list_images("./frames"))

for imagePath in imagePaths:

• #    загружаем изображение и уменьшаем его для уменьшения времени определения

• #    а также для увеличения точности

• #    оределение пешеходов на изображении

(rects, weights) = hog.detectMultiScale(image, winStride=(4, 4), padding=(8, 8), scale=1.05)

• #    выделяем пешеходов на изображении

for (x, y, w, h) in rects:

cv2.rectangle(orig, (x, y), (x + w, y + h), (0, 0, 255), 2)

cv2.waitKey(0)

Результат: