Определение объемов смешения трехкомпонентных сплавов на основе никеля через объемы смешения двухкомпонентных сплавов

Молярный объем сплава, а также объем смешения, являются одной из термодинамических характеристик раствора. Поэтому знание этих величин необходимо в ряде задач прикладного характера [1]. Целью данного исследования являлось нахождение зависимости молярных объемов и объемов смешения от состава сплавов. Определение этих величин для многокомпонентных металлических сплавов различного состава требует большого числа измерений, так как не существует теоретического метода расчета данных параметров. В данной работе показано, что можно определить молярный объем и объем смешения трехкомпонентного металлического сплава, зная состав сплава и соответствующие параметры образующих его двойных сплавов.

Методика эксперимента

Для исследований было приготовлено 77 трехкомпонентных металлических однофазных сплавов системы Ni – Cr – Mo. Концентрации компонентов были таковы, что все сплавы представляли собой твердые растворы на основе никеля. Плавка металлов производилась электрической дугой в медной водоохлаждаемой изложнице. Для определения периода кристаллической решетки были отобраны 38 сплавов так, чтобы они перекрывали всю область концентраций в шахматном порядке [2]. Период кристаллической решетки измерялся на приборе ДРОН – 3 по стандартной методике [3]. Как показали измерения, все образцы имели гранецентрированную

кубическую кристаллическую решетку. Для решетки такого типа, молярный объем рассчитывается по формуле [4]

V 23 = N A *а ³/4,                                             (1)

где V₁₂₃ — объем моля трехкомпонентного сплава, N_A - число Авогадро; а - период кристаллической решетки.

Обработав данные зависимости периода кристаллической решетки от состава сплава по методу наименьших квадратов, выявили следующую линейную зависимость:

а = (0,3524 + 0,0106 X Cr + 0,0406 X Mo ) нм,                               (2)

где 0,3524 нм – период кристаллической решетки чистого никеля; Х_Cr и X_Mo – мольные доли хрома и молибдена в сплаве. Абсолютная погрешность определения периода кристаллической решетки составила 1*10^-4 нм.

Для определения полного объема и объема смешения сплавов использовали формулы, полученные в результате следующих рассуждений.

Возьмем три компонента, обозначенные нижними индексами 1, 2 и 3 в количестве А, В и С молей соответственно. Объемы моля простых веществ V 1 - V₃. После сплавления объем одного моля стал равным V₁₂₃. При этом полученный объем для одного моля изменился на величину объема смешения AV₁₂₃ по сравнению с аддитивным значением. Исходя из закона сохранения количества вещества, можно записать

(A + B + C)АVm = (A + B + C)Vm - (AV1 + BV2 + CV3).(3)

Для двойных сплавов можно записать аналогичные равенства:

(A + B)АV = (A + BV - (AV + B^,

(A + C)АV, = (A + CV, - (AV + CV3),

'B . С)АV = (B + СV„ -(BV2 . CV,).(6)

Сложив правые и левые части уравнений (4) – (6), получим:

(A + B)AV„ . (A . С W . (B . С)А = (A + Ж + (A + C)V„ +

⁺ (B + C)V„ - 2(AV_{1 +} ^BV + CV , ),

Путем несложных преобразований из соотношений (3) и (7) получаем для идеальных растворов:

2( AV i + BV , + CV , ) = 2( A + B + C)(V_m - А V ;,, ) =

= ( A + B)(V 12 - А V ;, ) + ( A + C)(V 13 -А V 13) + ( B + C )( V ,3 - А V ,, ).

Примем, что уравнение (8) можно разделить на две независимые части, одна из которых связывает между собой молярные объемы трех- и двухкомпонентных сплавов, другая - справедлива для объемов смешения этих сплавов, т. е. справедливы соотношения

v

= 0,5

A + B

A + B + C

V₁₂ + 0,5

A + C

A + B + C

V₁₃ + 0,5

B + C

A + B + C

у

23 ^,

A V_m = 0,5

A + B

A + B + C

A V_n + 0,5

A + C

A + B + C

A V ₃ + 0,5

B + C A + B + C

A V 23 .

Упростим запись уравнений (9) и (10), перейдя к мольным долям:

V_l23 = 0,5(X , + X₂)V_I2 + 0,5(X , + X₃)V_I3 + 0,5(X₂ + X₃)V_B,                   (11)

A V 123 = 0,5( X । + X 2 ) A V 2 + 0,5( X । + X ₃) A V_u + 0,5( X 2 + X ₃) A V 23 ,          (12)

где X1, X2 и X3 - мольные доли первого, второго и третьего компонентов сплава.

Результаты исследований и их обсуждение

Используя данные зависимости периода кристаллической решетки от состава сплавов, по формуле (1) мы определили молярные объемы и объемы смешения для 77 сплавов системы Ni-Cr-Mo.

Затем были рассчитаны объемы моля двойных сплавов никель - хром и никель - молибден, а также их объемы смешения. Причем соответствующие величины для двойных сплавов определяли с учетом того, чтобы в тройных и двойных сплавах оставалось постоянным соотношение между X Ni и суммой X c _r + X_Mo. То есть для сплава никель - хром была постоянной величина Y₁₂ = X₂/(X₁ + X₂), а для сплава никель - молибден - величина Y₁₃ = X₃/(X₁ + X₃), где Х₁, Х 2 и Х 3 - мольные доли никеля, хрома и молибдена соответственно.

Для определения объема смешения AV₂₃ сплава хром - молибден использовали парциальные объемы 5V 23 , которые определяли по формуле

5V23 = Vl23 - (I - YV2 - Y3V13, где Y3 = X3/(X2 + X3), V12 и V13 определены соответственно при Y3 = 0 и Y3 = 1.

Экстраполируя величину 5 V₂₃ на случай X Ni = 0 при различных Y₃, мы получим гипотетическое изменение объема сплавов хром - молибден, если тип кристаллической решетки остался без изменений, как в тройных сплавах.

Обработка результатов эксперимента включала два этапа. Сначала производилась проверка соотношения (11). Результаты отображены на рис. 1-7. Полученные данные убедительно свидетельствуют о справедливости уравнения (11). Достаточно сказать, что расхождение между правой и левой частями уравнения лежало в пределах 0,6 – 0,8 %, т.е. ни для одного образца не превысило 1 %.

На втором этапе была произведена проверка соотношения (12). Было обнаружено, что уравнение (12) неприемлемо. Расхождение между правой и левой частями соотношения (12) составляло от 70 до 100 %. Более лучшее приближение дает уравнение (13), в котором отсутствует коэффициент 0,5. В этом случае расхождение между различными частями уравнения не превышало 20 %.

A V 123 = ( X I + X 2 ) A V 12 + ( X I + X 3 ) A V 13 + ( X 2 + X 3 > A V 23 .                    (13)

Отсутствие коэффициента 0,5 в соотношении (12) можно объяснить следующим образом. Полный объем сплава мы определили, просто просуммировав объемы образующих его веществ. Такой же подход к определению объема смешения неприемлем, потому что изменение объема обусловлено взаимодействием между атомами различных компонентов.

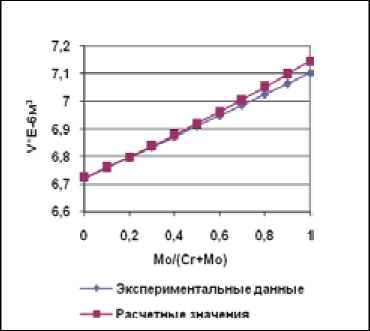
Рис. 1. Зависимость молярного объема сплавов Ni-Cr-Mo от соотношения между хромом и молибденом при содержании никеля 78 ат. %

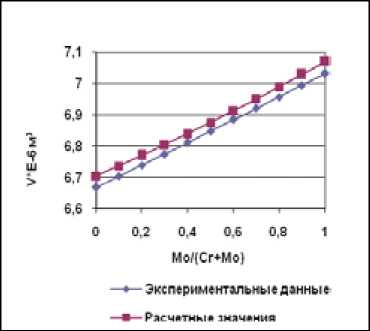
Рис. 2. Зависимость молярного объема сплавов Ni-Cr-Mo от соотношения между хромом и молибденом при содержании никеля 81 ат. %

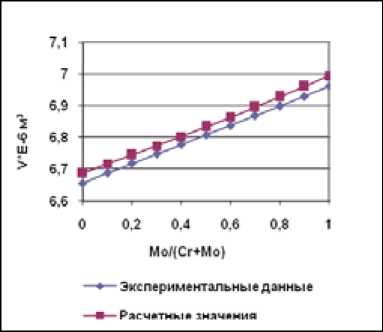
Рис. 3. Зависимость молярного объема сплавов Ni-Cr-Mo от соотношения между хромом и молибденом при содержании никеля 84 ат. %

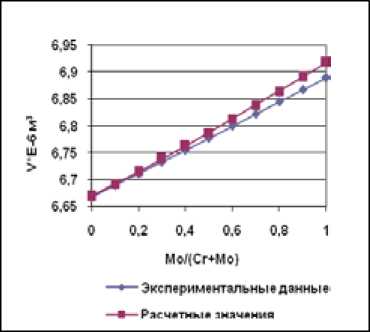
Рис. 4. Зависимость молярного объема сплавов Ni-Cr-Mo от соотношения между хромом и молибденом при содержании никеля 87 ат. %

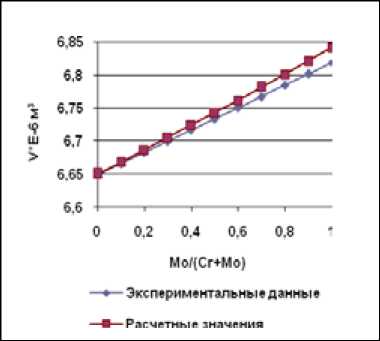
Рис. 5. Зависимость молярного объема сплавов Ni-Cr-Mo от соотношения между хромом и молибденом при содержании никеля 90 ат. %

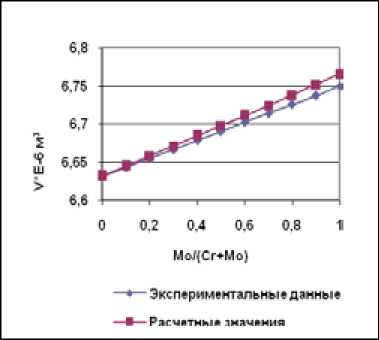
Рис. 6. Зависимость молярного объема сплавов Ni-Cr-Mo от соотношения между хромом и молибденом при содержании никеля 93 ат. %

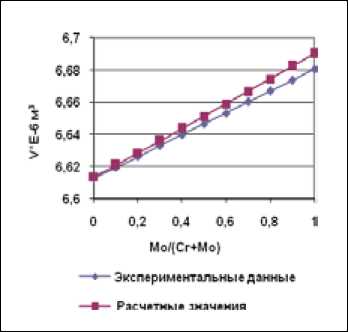
Рис. 7. Зависимость молярного объема сплавов Ni-Cr-Mo от соотношения между хромом и молибденом при содержании никеля 96 ат. %

В сплаве все три компонента взаимодействуют одновременно, т. е. схематично реакцию можно представить не в виде

А + В + С = АВС,

А а следующим образом: А + В + С =

В

С

На рис. 8 – 14 приведены графики зависимости объемов смешения от соотношения между хромом и молибденом. Как видно из этих графиков, значения объемов смешения, рассчитанных по формуле (12), очень отличаются от экспериментальных результатов, в то же время расчет по формуле (13) дает более приемлемый результат.

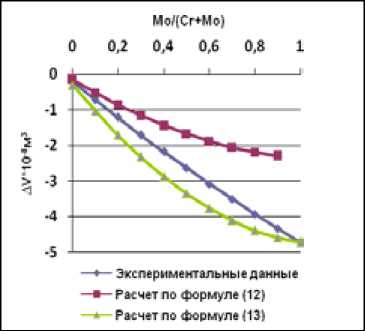
Рис. 8. Зависимость объема смешения сплавов Ni-Cr-Mo от соотношения Mo/(Cr+Mo) при содержании никеля 78 ат. %

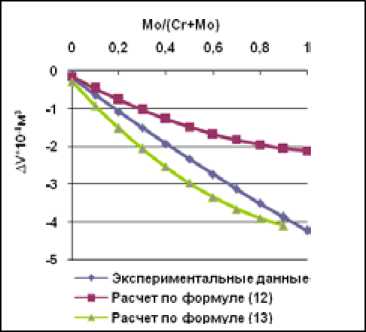
Рис. 9. Зависимость объема смешения сплавов Ni-Cr-Mo от соотношения Mo/(Cr+Mo) при содержании никеля 81 ат. %

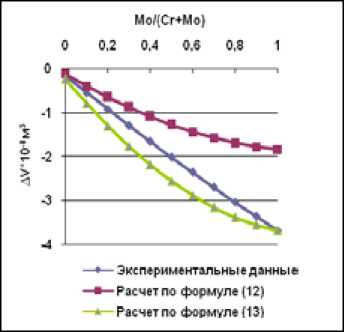
Рис. 10. Зависимость объема смешения сплавов Ni-Cr-Mo от соотношения Mo/(Cr+Mo) при содержании никеля 84 ат. %

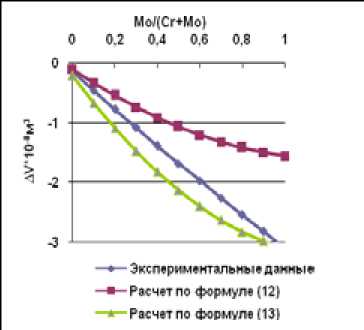
Рис. 11. Зависимость объема смешения сплавов Ni-Cr-Mo от соотношения Mo/(Cr+Mo) при содержании никеля 87 ат. %

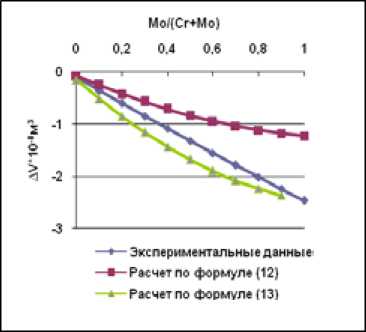
Рис. 12. Зависимость объема смешения сплавов Ni-Cr-Mo от соотношения Mo/(Cr+Mo) при содержании никеля 90 ат. %

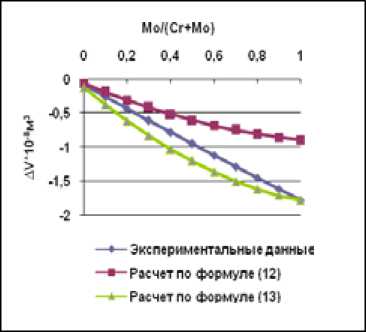
Рис. 13. Зависимость объема смешения сплавов Ni-Cr-Mo от соотношения Mo/(Cr+Mo) при содержании никеля 93 ат. %

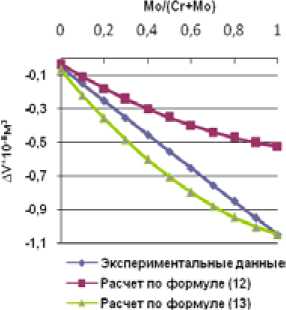
Рис. 14. Зависимость объема смешения сплавов Ni-Cr-Mo от соотношения Mo/(Cr+Mo) при содержании никеля 96 ат. %

Выводы

В результате проделанной работы нами были определены зависимости молярных объемов и объемов смешения от состава сплавов, а также установлено, что объем одного моля тройного сплава на основе никеля может быть рассчитан через величины объемов соответствующих двойных сплавов по формуле (11). В то же время объем смешения одного моля тройного сплава по подобной формуле не определяется. Для его определения необходимо использовать формулу (13). Аналогичный результат был получен для сплавов системы Ni-Fe-Mo [5].