Определение обобщённых перемещений в ортотропной пластине при действии сосредоточенной силы на базе{1,0}-аппроксимации

Тонкостенные элементы конструкций, изготовленные из современных композиционных материалов, широко применяются в объектах различного назначения, в том числе повышенного уровня ответственности при сложном нагружении. Об актуальности решения задач статики для пластин и оболочек свидетельствуют публикации последних лет [1, 2]. Использование композиционных материалов, обладающих резкой анизотропией упругих свойств, обуславливает актуальность построения уточнённых теорий пластин и оболочек, учитывающих явления, связанные с поперечными сдвигами и обжатием.

В настоящей работе для сведения трёхмерной задачи статики ортотропной пластины к двумерной используется обобщённая теория в варианте {1,0}-аппроксимации. Выбранный

«Московский физико-технический институт (национальный исследовательский университет)», 2021

подход является наиболее приемлемым для решения поставленной задачи, посколвку он не основан на каких-либо гипотезах, а использует метод И.Н. Векуа разложения искомых функций в ряды Фурье по полиномам Лежандра от толщинной координаты [3]. Преимуществом данного подхода является возможность рассматривать не только тонкие пластины, но пластины средней и большой толщины. При этом решение задачи может быть получено с произвольной, наперёд заданной точностью в зависимости от числа удерживаемых слагаемых в разложениях заданных и искомых функций. Из публикаций последних лет, использующих обобщённую теорию пластин и оболочек, в рамках которой искомые и заданные функции раскладываются в ряды Фурье по полиномам Лежандра, следует отметить статьи [4, 5].

В работе построено фундаментальное решение уравнений статики {1,0}-аппроксимации для случая безмоментного напряжённого состояния ортотропной пластины. Необходимость решения такой задачи обусловлена важной ролью, которую играют фундаментальные решения при исследовании различных граничных задач механики тонкостенных элементов конструкций, в том числе и находящихся под действием сосредоточенных силовых воздействий.

• 2.    Постановка задачи

Рассмотрим ортотропную пластину толщиной 2Һ в прямоугольной декартовой системе координат ж, у, z. В качестве исходной взята система уравнений {1,0}-аппроксимации. В рамках данного приближения компоненты напряжённо-деформированного состояния представляются в виде рядов Фурье по полиномам Лежандра Р^ от толщинной координаты z таким образом [3]:

е компоненты вектора перемещений:

п ж = пРо + ҺДж Р 1 , п_у = гРо + ҺдуР1, п_г = woРо, где п, г, wo, у_ж, ^ у — обобщённые перемещения пластины, из которых п, г, wo являются аналогами перемещений точек срединной поверхности, а у_ж, Ду — аналогами углов поворота нормали;

е компоненты тензора напряжений:

стж = NжРo + 3^ (ж ^ у), т = р0 + Р, ж 2Һ 0    2Һ2 1          ’ жу 2Һ 0     2Һ2 1’ тж^ = "2х°(Ро - Р2) (Ж ^ У)’ °г = °’ где коэффициенты разложений в ряды по полиномам Лежандра являются обобщёнными усилиями и моментами, из которых Nж, Ny, 8жу являются аналогами мембранных усилий: Мж. Му. Нжу — изгибающих и крутящего моментов: Qжo. Qyo — перерезывающих сил;

компоненты вектора объёмной силы:

^Ғ ж = 2Һ^Р 0 ⁺ ^ ⁽ж    ^Ғ = >■

E_x , Е у — модули Юнга для направлений ж, у соответственно; G_x y — модуль сдвига, характеризующий изменение угла между главными направлениями ж и у; v _xy, V y_x — коэффициенты Пуассона, характеризующие поперечные изменения (первый индекс указывает направление изменения, второй — направление действия силы, вызывающей это изменение);

• • уравнения равновесия

  дN1  3312 _ д^33

• 3.    Определение обобщённых перемещений

+ "я = -91, "5+ “X дЖ1    3X2         3X2

где 9 1 = 9 х /Е. 9 2 = q_y/Е .

Пусть на пластину действует сосредоточенная сила. Математической моделью сосредоточенных воздействий в механике является дельта-функция Дирака. Она стоит на месте функций нагрузки в правых частях разрешающих уравнений. Фундаментальные решения системы (1), (2) имеют определённый механический смысл — это решения задач о действии сосредоточенных сил на пластину [6]. Поэтому компоненты вектора объёмной силы берём в виде

9 з (ж 1 ,Ж 2 ) = 9 * й(ж 1 ,Ж2Пз = 1, 2), (3) где 5(ж 1 ,Ж 2 ) — двумерная дельт a-функция Дирака, 9* = const.

Подставляя соотношения упругости в перемещениях (1) в уравнения равновесия (2), получим уравнения равновесия в перемещениях, которые с учётом правых частей (3) имеют вид д2г 3x1дж2

д ²    „  д²

- 9 * 5(ж і ,Ж 2 ),

• ^В 1 дЖ | ^{+ В12} дЖ |/ " ^{+ (v$y В1 + В12)}

• ^д 2 U      ^Vxy_R^д 2         ^{д 2}          *

(^VxУ^{B1 + В12)} дж і дж 2 ⁺ (vуx^B1 дЖ 2 ^{+ В12} aXJ^ ^V = ^{-92 5}(^Ж1'^Ж2)-

Применим к системе (4) двумерное интегральное преобразование Фурье [7]:

*

(В 1 С 1 ² + В 12 € 2 и + (VxуB 1 + В 12 ) Ф^г = 9 1 , 2^

(VxуB 1 + В 12 ) C 1 C 2 U + (^VXУB 1 e 2 + В 12 ^ 1 ²) Г = 91 .

V yx                    2Л

Решая полученную систему линейных алгебраических уравнений, найдём трансформанты обобщённых перемещений:

где

• 1    V

  ^и = 9 R R 1 --- ^В 1 9 1 ^Ф 1 ^(С 1 , ^ 2 ) ^{+ В} 12 9 1 ^Ф О ⁽€ 1 ^,€ 2 ^{) - (v} xу ^B 1 + ^В 12 ) 9 2 ^ф 2 ⁽€ 1 , € 2 ) , ²^^в 1 ^в 12   ^V y _X

  • ^V = 9 R R I ^В 1 9 1 ^КдЫ ^{+ В} 12 9 1 ^ф 1 (< 1 , ^ 2 ) ^- (У х-у ^ ^{+ В} 12 ) 9 2 ^(Д,^) , 2лВ 1 В 12

^C 1               ^                         ^С 2

Ф о ⁽^ 1 ,^ 2 ⁾ =

2   22  2   22

⁽S 1 ^{+ о} 1 ^€ 2 Ж1 ^{+ o} 2 S 2 )

.^^-

^ф 2 ⁽€ 1 , € 2 ) =

, ^ф 1 (^ 1 , б) = € 1 ^ 2

2      2у2    2      2у2 ’

Ж ^{+ 0} 1 S 2 Ж1 ^{+ у} 2 4 2 )

° 1 , 2 = 2V ^^Vxy ^(E x ^/G xy ^-

2      2 2    2      2 2 ’

Ж ⁺ ЩS 2 Ж1 ⁺ ^ 2 4 2 )

^2vyx) Т ^^v2 y ^(E x ^/G xy  ^2vyx)   ^4vxy ^Vyx •

Методику обращения покажем на примере первой из функций (6). Заметим, что

^Ф0^{( €} 1 ^,€ 2⁾ = ""2

-

где

— {° 2 ^Ф 1 ^(€ 1 ^,€ 2 ; Ж) ^o 1

-

У 2 Ф 1СДД2 ; о-1)} ,

1 ^ф і ^(с і ,^с 2 ; o k ) = _{t2     2}.2 ^(к = 1, ²⁾.

^C 1 ^{+ У} к ^€ 2

Для нахождения оригинала функции Ф1 применим к ней формулу обращения для двумерного интегрального преобразования Фурье [7]: ^ ^

Ф1(ж1,ж2; п к ) = ф / / exp'.+■ «.              (7)

2 л J J      €2 + о^

—га —га

В двойных интегралах (7) выполним такие замены переменных в пространствах оригиналов и трансформант:

€1 = ’И, €2 = —, Ж1 = У 1 , Ж2 = d_k у2.                           (8)

О к

Выделим в интегралах (7) чётные и нечётные части и перейдём в полярные системы координат по формулам

У1 = г cos р, у₂ = г sin р, щ = p cos Ө, у₂ = p sin Ө,                   (9)

тогда

^/2   ^ Ф1 =--- гіӨ - cos (rpcosp cosӨ) cos (rpsinpsin Ө)dp•              (10) ^Ок J    J p 00

Применяя разложение Якоби-Ангера [8]:

га cos (ж cos р cos Ө) cos (ж sin р sin Ө) = Jо(ж) + 2 ^^ (—І^Дж) cos 2пр cos 2пӨ

П=1 и учитывая значения интегралов от тригонометрических функций 7т/2

/ cos2пӨdӨ =   ^/2’7 = 0’

0, п = 1, 2, ..., преобразуем функцию (10) к виду

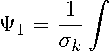
га ^о^гір. р

Чтобы вычислить данный интеграл, используем понятие конечной части (f.p.) от расходящегося интеграла [9]:

Ф1 = — f.p. / ^J 0 ^(rp) dp = — / lnpJ 1 (rp)dp = —-ln ^ЭГ,            (11)

^п к J ^{p        п} к J                  ^п к   ²

где С = lny = 0,5772... — константа Эйлера.

Вернёмся в (11) к переменным Ж1, Ж2 согласно формулам (9) и (8), тогда окончательное выражение для функции Ф1 примет такой вид:

1   7ТпкЖІ+^І

Ψ1 = ln

Ок        2ок а оригиналом первой из функций (6) является

(к = 1, 2),

Φ0 =

П2

—

эУ-

02 ln----

О2Ж1 + ж 2 20 2

—

дУо^ж^+ж2

О1 ln —201—) •

Аналогично определяются оригиналы других функций (6):

Φ1 =

П2

—

п12

(£ ln ^

О2ж1 + ж2

2о 1

—

Φ2 = п2

—

п12

„ X „ ^О 2 ^Ж 1 arctan

Ж2

—

у ln TViiy+H П2         2П2      ) 1

О1Ж1 arctan

Ж2

.

• соотношения упругости в перемещениях дп       дг             дг       дп              дп

^N 1 = ^В 1      ⁺ У жу      ’ ^N 2 = ^В 2       ⁺ У уж      ’ S 12 = В 12

дж і       Эж 2 у            \Эж 2       дж і у             \дж 2

где

АТ _ ^Nж АТ _ ^Ny С _ ^жу р /Ж ЕН

^N1 = Eh’^N 2 = ЕҺ’ ^S1 2 = Еж'^Е = ^VPжPУ’

дг

+      , (D джі

В і

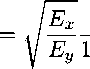
^У жу ^У уж

,В 2 =

/Еу_

V Еж 1

^У жу ^У уж

’ ^В 12 =

2^жу Е

Таким образом, оригиналы обобщённых перемещений на основании (5) имеют вид

^П = 2лВ 1 Вц

^ = -------

2^В 1 Вц

] -^В^ФДж^жД + В12діФо(Ж1,Ж2) — (v_xyB 1 + Вц)^ Ф2(Ж1,Ж2) > ’

I ^v yx                                                                         )

{B 1 f* Фо(Ж1,Ж2) +В 12 7 * Ф 1 (ж 1 ,Ж 2 ) — (v_xyB 1 +В12)д*Ф2(Ж1,Ж2)} ,

где функции Фо — Ф2 определяются по формулам (12), (13).

• 4.    Анализ результатов численных исследований

Численные исследования проведены для реальных ортотропных материалов: стеклопластиков типа СТ-19-55 и С1-10-65 [10]. Данные для указанных материалов приведены в табл. 1.

Т а б л и ц а 1

Данные для ортотропных материалов

Стеклопластик	^Ж^	^Ж	Ех, МН/м2	Gxy, МН/м2
С1-19-55	0,128	0,161	2,5 • 104	4,3 • 103
С1-10-65	0,122	0,17	3,25 • 104	6,1 • 103

Для исследования влияния упругих констант на обобщённые перемещения в ортотропной пластине (14) при сосредоточенных силовых воздействиях положим q* = q 2 = 1. Результаты расчётов представлены на рис. 1, 2 в виде графиков изменения обобщённых перемещений и, а вдоль ос и абсцисс ($2 = 0)- Сплошные линии соответствуют стеклопластику С1-10-65, а пунктирные — СТ-19-55.

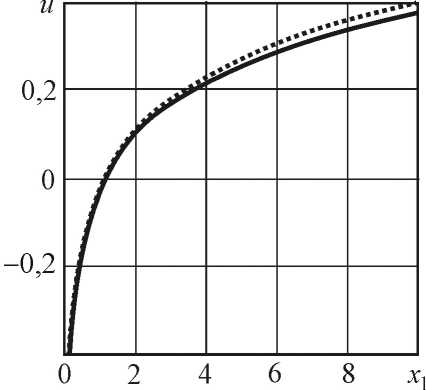
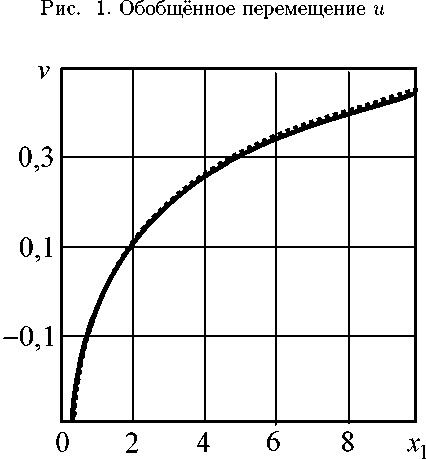
Рис. 2. Обобщённое перемещение г

Из данных графиков (рис. 1, 2) можно заметить, что с увеличением модуля сдвига G_xy обобщённые перемещения ина возрастают.

• 5.    Выводы

На основании проведённых исследований можно сделатв такие выводы:

• 1.    Впервые построено фундаментальное решение уравнений статики для случая безмо-ментного напряжённого состояния ортотропных пластин на базе обобщённой теории в варианте {1,0}-аппроксимации при действии сосредоточенной силы.

• 2.    Проведены численные исследования, демонстрирующие влияние упругих постоянных ортотропного материала на обобщённые перемещения, возникающие при безмомент-ном напряжённом состоянии ортотропных пластин.