Определение односторонней скорости света

Есть одна интересная тема в физике – односторонняя скорость света. Считается, что даже дать определение этой односторонней скорости нельзя [1]. Это происходит из-за того, что непонятно как синхронизировать часы, используя движение светового сигнала только в одну сторону. Так же непонятно как производить измерение длин. Поэтому определения нет. Просто приняли считать её равной двусторонней скорости. Считается, что если найти разные способы задания односторонней скорости света и дать определение этой скорости, то это не повлияет на предсказание результатов эксперимента. Если же процедуру синхронизации и процедуру измерения длины задавать не правильно, тогда можно обнаружить влияние анизотропии скорости на результат эксперимента. Так как в этом случае измерения будут не расстояния и времени.

Оглавление

1.    Причина возникновения противоречия

Противоречие в том, что теория предсказывает независимость результата эксперимента от того какая скорость света – изотропная или анизотропная. Это предсказание используют теории Эйнштейна – СТО и ОТО, в частности при построении пространства событий. Однако легко показать зависимость длины измеряемого объекта от вида скорости света в случае «одновременной» процедуры измерения длины Эйнштейна.

Понятно, что возможно и нет анизотропии скорости света, и все расчёты с помощью двухсторонней скорости света верны. Но если есть, а все считают, что это ни как не повлияет. И если при этом обнаружится, что есть варианты, что влияет на предсказание результатов эксперимента. Тогда требуется коррекция теории. Поэтому предлагается рассмотреть вариант анизотропии скорости, когда скорость светового сигнала (от) наблюдателя отличается от скорости светового сигнала (к) наблюдателю.

Для начала вспомним, что для односторонней скорости света не написали определения, то есть, его просто нет (см. [1]). Это объясняется тем, что считается, что введение любого определения для односторонней скорости света не изменит предсказания конечного результата. Проверим это утверждение в случае измерения длины движущегося стержня. Сначала вспомним процедуру Э., синхронизации часов.Детали расписывать не буду (она известна): Рассматриваются две точки А и В. В момент времени ТА из А посылают в сторону В световой сигнал, затем сигнал отражается в В и идет в сторону А и приходит в А в момент времени Т2А. Часы считаются синхронизированными по Э., если в момент разворота сигнала на часах точки В устанавливается время

Т В =(Т А +Т 2А )/2. (1)

Теперь вспомним процедуру Э. измерения длины движущегося стержня. (Так же детали расписывать не буду).

Рассматривается предполагаемая траектория движения стержня в виде прямой, все точки прямой с синхронизированными часами и с фотоаппаратом. Все погрешности не учитываются. Стержень движется и в определённый момент времени на часах – фотографирование. Фиксируются точки – где начало и конец стержня, затем измеряется расстояние между этими точками.

Пока я напоминал всем известные процедуры и выводы из процедур. Теперь попробуем рассмотреть эти процедуры в случае разных скоростей света, направленных (от) наблюдателя и (к) наблюдателю, такую скорость света назовём анизотропной.

Расчёт в цифрах будет наглядней, чем в общем виде, тем более, что физики с которыми я общался по данному вопросу – все хотели реальные данные (хоть и мысленного эксперимента). Анизотропия скорости света состоит в том, что от точки наблюдения свет идёт с одной скоростью, а к точке наблюдения идёт с другой скоростью. Поэтому, например, рассмотрим скорость света от наблюдателя в 2 раза больше, чем к наблюдателю. Чтобы теперь разобраться с одновременностью хода часов, хоть там

Э. и заявлял, что они синхронизированы и одновременны, рассмотрим мысленный эксперимент.

Рассмотрим траекторию стержня в виде прямой, рассмотрим стержень, который проходит точку наблюдения «0» со скоростью почти равной скорости света в эту сторону (для простоты расчёта, ведь можно измерять и в долях скорости света, но тогда возникнут лишние коэффициенты). Так как не рассматриваем релятивистские изменения, то в расчетах можно писать просто равной скорости света в эту сторону (а теоретически можно рассматривать и световую волну). Считаем, что стержень длиной примерно 6 световых секунд (сс) по СТО (в длинах двухсторонней скорости света) при этой скорости для точки «0». То есть в покое стержень длиннее, а так как существует (мы же проверяем СТО) в теории сокращение длины при некоторой скорости движения, то длина стержня становится равной 6сс для неподвижного наблюдателя. А примерно равно, так как считаем с небольшими погрешностями, которые не влияют на результат, так как берём их (погрешности), например, в пределах 1% от рассматриваемых цифр. Это сокращение длины – единственный учет релятивистских скоростей, а так как считается, что средняя (изотропная) скорость света известна и известно отличие скорости стержня от этой скорости света, то возможен теоретический расчёт по СТО. Эта длина необходима только для сравнения с длиной стержня, полученной при расчете с анизотропной скоростью света. Далее всё будет рассматриваться в неподвижной ИСО и отличие скорости стержня от скорости света в пределах 1% можно не учитывать.

Как движется стержень и применяются синхронизации, я описал двумя способами, чтобы было понятней.

Первый способ – пространственно временные диаграммы:

Рис. 1 показывает изменение времени при изменении расстояния синхронизирующего сигнала от точки «0» в случае изотропной скорости света.

Рис 2 показывает изменение времени при изменении расстояния синхронизирующего сигнала от точки «0» в случае анизотропной скорости света.

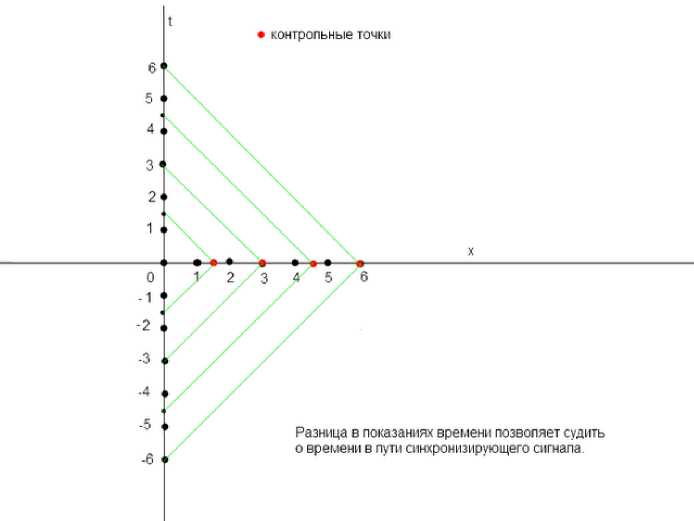
Рис. 1.

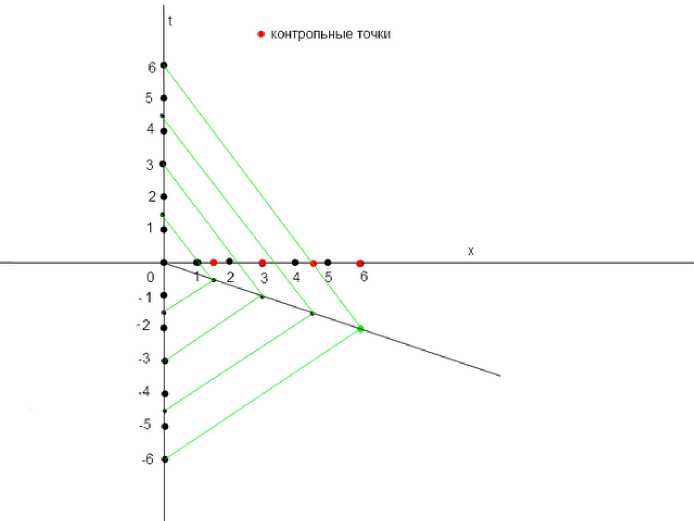
Рис. 2.

Сравнивая рис. 1 и рис. 2 видем, на сколько сигнал с анизотропной скоростью обгоняет сигнал с изотропной скоростью. То есть в каждой контрольной точке ко времени движения сигнала добавляется дополнительное время, связанное с процедурой синхронизации по Э. Так же ясно, что торец, двигаясь почти со скоростью светового сигнала, приходит в контрольные точки вместе с этим сигналом, а значит и ко времени движения торца добавляется это время.

На рис. 3 изображены точки движущегося стержня (взяты два положения стержня).

На рис. 4 точки этого стержня с учётом дополнительного времени.

При рассмотрении рис. 4 становится понятно, что изображённые на рисунке торцы «1» и «2» окажутся в контрольных точках «0» и «4», но при этом часы будут показывать разное время. А согласно процедуре измерения длины – время на часах должно быть одинаковое.

Это означает, что торец «2» засекли раньше, то есть длина стержня изменилась.

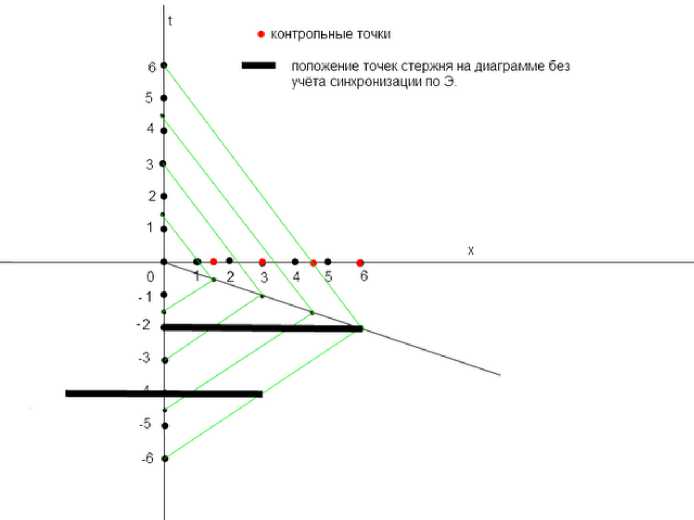
Рис. 3.

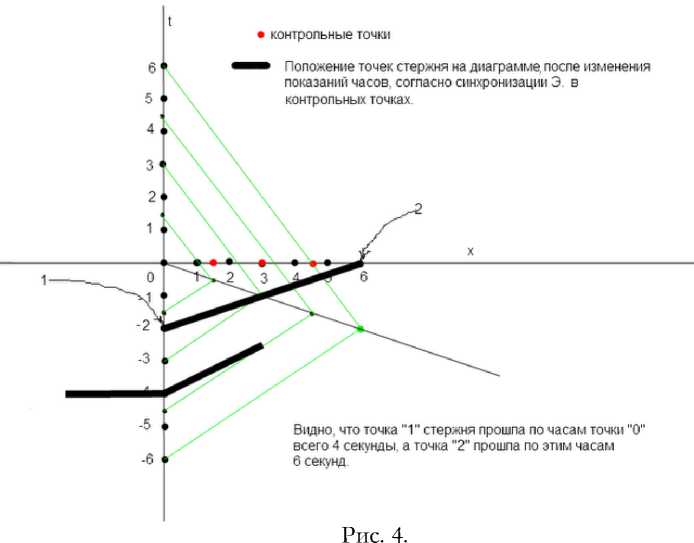
Второй способ – описание движения стержня.

Будем, чтобы было понятно и не возникло вопросов, через 11 секунд после «синхронизации» по Э. двигать посекундно стержень и записывать показания всех часов. Предварительно наметим контрольные точки. На прямой расставим точки через 1,5 сс, с помощью двухсторонней скорости. Наметив, таким образом точки, выбираем одну, как точку А. Теперь необходима синхронизация по-Э. Так как скорость сигнала (от) точки А в два раза больше, чем скорость сигнала (к) точке А – так договорились, то при синхронизации: время движения сигнала (от) точки А до следующей точки=1секунде, время движения сигнала (к) точке А от следующей точки=2секунды (и так между всеми контрольными точками), среднее время=1,5 секунды. Запишем, что ставится на часах в контрольных точках при синхронизации Э.

Точка обозначается кавычками:

«0» ставится 0, «1» - 1,5, «2» - 3, «3»- 4,5, «4» - 6 секунд (2)

Теперь запускаем стержень через 11 секунд после начала синхронизации по Э.

Так как условились, что движение стержня в расчетах записывается, как со скоростью света, хоть оно немного меньше.

Поэтому считаем, что каждую контрольную точку торец стержня проходит так же, как и синхронизирующий сигнал, только позже на одно и то же время. Это время выбрали, например, 11 секунд (такое число легче заметить в расчётах). Теперь поэтапно, через секунду отмечая время, двигаем стержень.

Записываем точки так. Первая точка – куда дошёл торец стержня, далее контрольные точки, которые прошёл первый торец и время в этих контрольных точках через секунду от предыдущего значения (ведь часы неподвижны и время в них идёт одинаково). Естественно время в контрольной точке, куда дошёл стержень надо устанавливать по синхронизации Э., а далее на этих «синхронизированных по Э.» часах идет добавка секунд: дошёл торец до «0» (это точка А) время - 11 секунд, дошёл торец до «1» (прошла секунда) в «0» - время на часах =12сек, в «1» время на часах =12,5сек Поясняю: добавили секунду к значению в «0» и установленное время часов «1» к 11секундам, дошёл торец до «2» (прошли 2 секунды) в «0» - время на часах =13сек, в «1» время на часах =13,5сек, «2» =14.

Поясняю: добавили ещё по секунде к предыдущим значениям часов «0», «1» и 11 секунд к установленному времени на часах точки «2», далее аналогично, дошёл торец до «3» (прошли 3 секунды) в «0» - =14сек, в «1» =14,5сек, «2» =15сек, «3» =15,5сек, дошёл торец до «4» (прошли 4 секунды) в «0» - =15сек, в «1»- =15,5сек, «2»- =16сек, «3»- =16,5сек, «4»- =17 сек                                       (3)

Понятно, что при использовании движения только в одну сторону предполагаемой одновременности часов нет на ожидаемых расстояниях. Нам же нужна одновременная фиксация торцов стержня. В нашем примере получается, что для показаний часов, например, 15 секунд (то есть 15 секунд должны быть на часах переднего и заднего торца).

Смотрим точки, где было это значение времени на часах при прохождении точек торцами:

Задний торец, понятно, - это точка "0".

Передний торец, видим, что не дошел немного до точки "3", так как оказался в точке "3" уже, когда на часах было 15,5 сек.

То есть по процедуре Э. зафиксированы торцы в точках "0" и чуть раньше точки "3".

А по теории Э. торцы должны быть зарегистрированы строго в точках "0" и "4".

То есть явное противоречие. И ясно, что небольшие погрешности роли не играют.

Легко видеть, как рассчитать одностороннюю скорость. Понятно, что расхождение практического результата с теоретическим результатом тем больше, чем больше разница в скоростях (от) и (к) наблюдателю. Расчет элементарный: берётся теоретическая длина L стержня и практически измеренная длина стержня H.

Ясно из приведённого примера, что

(L/w-L/V)=(L-H)/w,                                   (4)

Или L/V=H/w,                                 (5)

где w- средняя (двухсторонняя) скорость, а V – скорость (от) точки наблюдения – точки «0». Так как полученная формула зависит от длины, определённой через двух стороннюю скорость, и кнопки переключения от изотропной к анизотропной скорости света у нас нет. Тогда сразу встает вопрос – как измерялась длина через двухстороннюю скорость.

Ясно, что только этим уравнением не определить одностороннюю скорость, так как оно даёт только соотношение, при котором как раз и неразличима односторонняя и двухсторонняя скорость. Но можно одновременно провести аналогичное измерение по другому направлению односторонней скорости. У нас ведь предполагается до точки «0» одна скорость светового сигнала, а после точки «0» - другая, так как она перешла от скорости (к) наблюдателю к скорости (от) наблюдателя. Для расчета L – длины с помощью двухсторонней скорости в случае до точки «0» и в случае после точки «0» используется абсолютно одинаковый способ. Поэтому для получения формул используем величину L, которую потом из формул исключим.

Понятно, что можно рассмотреть аналогичное измерение на подходе к точке «0», то есть рассматриваем эксперимент со скоростью света (к) наблюдателю, обозначим её буквой v. В этом эксперименте аналогично получим (в этом случае измеренный реальный размер будет h):

L/v=h/w или L=h(v/w)

Тогда

V=v(h/H)=kv, где k=h/H                            (6)

Ясно что средняя скорость на длине пути L определяется так: t1=L/V, t2=L/v, тогда w=2L/(t1+t2)=2vV/(V+v)=v(2k)/(1+k)=V2/(1+k) (7)

Формулы (6) и (7) дают связь односторонних скоростей и двухсторонней скорости. Так же понятно, что сильного различия в скоростях нет, иначе, судя по-формулам, её легко было бы обнаружить.

Но теоретически есть зависимость результата эксперимента от того изотропна скорость света или анизотропна. А этот результат мы и получали – он очень важен, так как дает понимание, что синхронизация Э. в случае анизотропной скорости света дает сбой.

2.    Правильная синхронизация

Предлагается одна из возможных коррекций синхронизации часов Э. Так как понятно, что при разных односторонних скоростях света синхронизация часов по Э. не соответствует действительности. Это происходит из-за того, что часы в точке «0» «синхронизируются» с другими точками с приходом обратного сигнала. Но при измерении длины стержня происходит просто фиксация положения стержня в некоторый момент времени без сообщения обратным сигналом достижения какой-то точки передним торцом стержня. Избежать несоответствия можно только, если ввести синхронизацию часов с использованием скорости движения светового сигнала только в одну сторону. То есть необходимо ввести «одностороннюю синхронизацию».

«Односторонняя синхронизация» задаётся проще, чем по процедуре Э.: часы выставляются на ноль с приходом сигнала из какой-либо точки, но таким образом синхронны только часы, расположенные по пути следования сигнала и только в сторону следования сигнала. Меняется направление сигнала, тогда меняется и синхронизация. В этом, конечно, неудобство: каждый раз новая синхронизация.

Понятно, что с помощью такой синхронизации не задать скорость и не задать единицу длины. Для их задания используется двухсторонняя скорость, к тому же ведь надо с чем-то сравнивать одностороннюю скорость. Односторонняя скорость связана коэффициентом с двухсторонней скоростью. А единица длины – метр, определяется точно по известной в физике формулировке – немного изменённой. Метр — единица измерения длины и расстояния в СИ. Метр равен расстоянию, которое проходит свет в вакууме в один конец эталона, там отражается и проходит в исходную точку за промежуток времени, равный (2)/(299792458) секунды. Это определение в случае равенства односторонних скоростей в точности повторяет общепринятое определение в физике.

При односторонней синхронизации и такой формулировке длины, легко измерять длину световым сигналом. Процедура проста: посылается сигнал и отражается в исходную точку, по времени задержки рассчитывают длину, исходя, естественно, из величины двухсторонней скорости.

Замечу, что преобразования координат и соответствующие выводы, которые следуют из предложенной синхронизации и этих преобразований изложены в "Теории времени", которая тоже опубликована в данном выпуске.