Определение оптимальной массы оболочек взрывных камер

взрывчатого вещества. Схемы случаев и необходимые параметры приведены на рис. 1 и 2. Сферическая оболочка (рис. 1) имеет радиус R C и толщину δ C , в её центре расположен сферический заряд взрывчатого вещества произвольной массы M C , которое имеет удельную теплоту взрыва Q 0 . Цилиндрическая обечайка бесконечной длины (рис. 2) имеет радиус R Ц , толщину δ Ц и высоту H , на её оси симметрии расположен заряд ВВ произвольной массы M Ц (выражается через r 0Ц и Н ) который имеет удельную теплоту взрыва Q 0 . В расчетах будем считать Н= 1 м, т.е. будем рассматривать погонные величины.

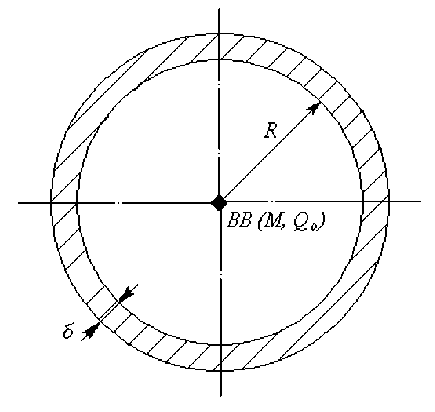
Рис. 1. Параметры сферической оболочки

Для обоих случаев определим оптимальную с точки зрения экономии массы толщину стенки оболочки при условии обеспечения заданной прочности по допускаемым напряжениям.

Будем считать, что в сферической оболочке реализуется двухосное напряженное состояние, напряжение σ r примем равным нулю (оно действует вдоль радиуса). В цилиндрической оболочке напряженное состояние одноосное – напряжение σ r и σ z примем равными нулю. В ходе расчета величины в формулах для сферической оболочки будут содержать индексы « с », а для цилиндрической – « ц ».

_{о —} м ц e 2ог₀

^{GфЦ   п}р5 ц • ^Rц ^а о

Эквивалентные напряжения

^СТ эквС ^— ^(^ фС ) + ⁽ ^ ес )    ° фС ° ес ^— ° фС

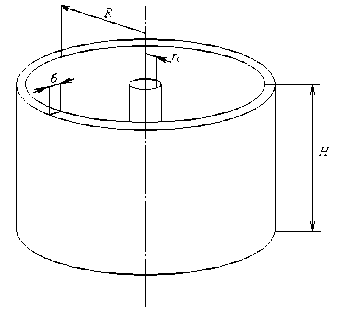
Рис. 2. Параметры цилиндрической оболочки

° эквЦ ^— ° ф Ц

Для обеспечения прочности оболочки, эквивалентные напряжения не должны превышать допустимых значений о _экв <  [ ст ] . За допустимые значения примем предел упругости при циклическом нагружении (N>10⁶ циклов). В результате получим следующие зависимости

[о] —

2 ^ /1 - ц

M С E Q 0

^Р ^ С ⁽ R c ) ^а о

Аналитическое решение . Итак, согласно [1] имеем:

[ст] —

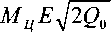
^ПР § Ц • ^R Ц ^а о

^о ф ц

2     Р о ⁽ r o с ) 3 E4Q

-----;           •-------------:------—--------

3^1 - ц рб _с ( R_C ) a 0

P o ⁽ r o ц ) V ² Q о ^E

р5 ц • ^R ц а о

Здесь: ρ 0 и r 0 – соответственно плотность и радиус заряда ВВ. Е – модуль упругости. ρ – плотность материала оболочки. а 0 – скорость звука в материале оболочки. Формулы (1) справедливы для тонкостенных оболочек (R≥10δ). Масса заряда ВВ

M e ^— 3 ⁿP o ⁽ r o С ) ^,

M ц ^{— п}Р о ⁽ r o Ц ^{) 3} H

Н – высота цилиндрической оболочки (а также, соответственно, и высота заряда). Будем считать H= 1 м, т.е. далее во всех формулах для цилиндра М Ц будет являться величиной погонной массы заряда (размерность кг/м) и выражаться форму-²

лой M ц — пр ₀ ( г _о ц ) . С учетом (2), формулы (1)

примут вид

° ф с ^— ° е с

1      M C E Q 0

----------,            •-----------:-------—------

² П ¹ - ц Р⁵ С ^{( R}C ) ^а о

Введем некоторые коэффициенты K 1 (сферическая оболочка) и К 2 (цилиндрическая оболочка)

K 1 —

1     M C E Q 0

•

2П1 - ц   Ра о[о]

K 2 —

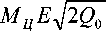
пр- а о [ о ]

которые определяют физические свойства материала оболочки, а также свойства и параметры заряда ВВ. Формулы (4) примут следующий вид

§ с

⁸ Ц

K 1

(RC17

,

K 2

RЦ

Формулы (5) определяют необходимую толщину стенки, обеспечивающую заданную прочность в зависимости от радиуса оболочки. Выразим массу сферической и цилиндрической оболочки через известные размеры

me — 4 ПР[(Rc + 5С )3 -(Rc )3 ]

,          (6)

тц — ПР- H[(RЦ + 5Ц )2 - (RЦ )2 ]

.

Высоту Н также примем равной единице. Тогда m Ц – погонная масса цилиндрической обечайки с

Таблица 1. Механические и физические характеристики материалов оболочки камеры

Название Символ Величина коэффициент Пуассона μ 0,3 плотность ρ 7800 кг/м3 скорость звука в металле оболочки а0 5000 м/с модуль упругости Е 2,1 ∙1011Па размерностью кг/м, тц = пр- [(Rц + 5Ц)2 -Rц2]. Подставив в формулу (6) зависимость (5), получим

взрывчатому веществу тротилу. С учетом вышесказанного, получим

4 Л . т_с = — пр I R_c + С 3 I С

K 1 I 3

( R c ) " 1 ⁴ R^c ’

K 1 = 2,099 - 10 6

M

- -------------