Определение ординат ядер Вольтерра при идентификации нелинейного динамического объекта с учетом отличия автокорреляционной функции тест-сигнала на основе двоичной м-последовательности от дельта функции

Для описания динамических нелинейных объектов применяют различные математические модели, в том числе отрезки ряда Вольтерра [1, 2, 3]:

∞

y (t) = h 0 + J h. (т ) • x (t - т) d т +

∞∞

J Jh 2 (т1, т 2) • x (t - т1) • x (t - т 2) d т dT 2.

Здесь x ( t ) и y ( t ) - входной и выходной сигналы объекта. h 1 ( т ) - ядро Вольтера первого порядка (импульсная переходная функция, ИПФ), h ₂ ( т 1 , т ₂) - ядро второго порядка.

Для раздельного определения ординат ядер Вольтерра используется корреляционный метод. При идентификации используют кусочно-постоянные тест-сигналы небольшой амплитуды, ортогональные к сдвигу, на основе псевдослучайных двоичных М-последовательностей [1,2], не нарушающие текущее функционирование объекта, реакция объекта измеряется один раз на такте тест-сигнала Δ t . Тогда:

5 У ^[ i ^] • ^{x [} i ^- j ^]

h[ j ] =,

5 x ²[ i - j ]

‘p"

5 y [ ‘ ] • x [ ‘ - k ] • x [ ‘ - 1 ]

h[ k, 1 ] p,

5 x 2[ ‘ - k ] • x 2[ ‘ -1 ]

i = 0

где y [ i ] и x [ i ] – замеры реакции объекта и тест-сигнала, h [ j ], h [ k , l ] – ординаты ядер Вольтерра, р – число тактов тест-сигнала.

В тестирующий сигнал на базе двоичной М-последовательности дополнительно вводятся такты, обеспечивающие независимое и несмещенное вычисление оценок h [ j ], h [ k , l ] и h [ k , k ], а также для устранения погрешности из-за неправильного определения начального состояния объекта перед тестированием [2, 3].

На рис. 1 в качестве примера приведен тестирующий сигнал, содержащий двоичную М-пос-ледовательность с характеристическим полиномом F ( x ) = х ³+ х +1 и дополнительные такты. Штрихами обозначены моменты измерения выходного сигнала объекта. Реально в тест-сигна-лах используются М-последовательности с периодом более 2¹⁰ [2].

Алгоритмы (2) получены при допущении, что автокорреляционная функция (АКФ) ортогонального к сдвигу тест-сигнала есть δ -функция

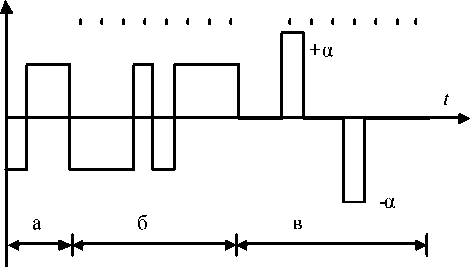
Рис. 1. Тест-сигнал на базе двоичной М-последовательности: а – формирование начальных условий, б – период М-последовательности, в –дополнительные такты

Дирака, что является упрощением. В отличие от 5 -функции Дирака АКФ кусочно-постоянного тест-сигнала имеет не нулевые значения в интервале (- At , A t ), а не только при т = 0.

Целью этой работы является получение аналитических выражений для определения ординат ядер Вольтера с учетом отличия АКФ кусочно-постоянного тест-сигнала от 5 -функции Дирака.

Ядра Вольтера определяются из уравнений Винера-Хопфа [1]:

T

К„ (г) = Jh (s) • Kx (т - s) ds.     (3)

что привело к результату:

h[ j] *

Kxy ( j •At) At

h[0]»

2 • Kxy (0) At

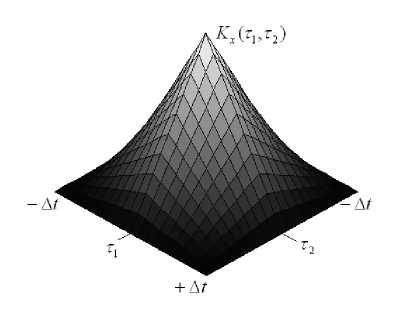
Рассмотрим вычисление ординат ядра Воль-терра второго порядка по соотношению (4). Выражение для АКФ второго порядка (Рис.2,б) кусочно-постоянных сигналов получим аналогично (5):

0, т1 > At, т2 > At

^Kxy ^{( т} 1^{, т} 2 ) =

^TT                                       (4)

J J h (si, s2) • Kx (Ti - s 1,т2 - s2)ds 1 ds2.

0 0

^Kx ^{( т} 1^{, т} 2 )

^{(1 -} W^{1 -} W ^т 11 - ^{A t ,} И - ^A . A t    A t

Здесь K x ( т ) и K x ( т ₁, т ₂) - АКФ тест-сиг-нала первого и второго порядков, K_xy ( т ) и ^Kxy ^{( т} 1^{, т} 2 ) – взаимокорреляционные функции реакции объекта и тест-сигнала первого и второго порядков, Т – период тест-сигнала.

Для ядра первого порядка (импульсной переходной функции) вычисления по (3) для тест-сигнала на основе М-последовательности с учетом отличия его АКФ от 5 -функции приведены, например, в [4]. На рис. (2, а) приведена АКФ первого порядка K x ( т ) кусочно-постоянного тест-сигнала, ортогонального к сдвигу, в (5) дано аналитическое выражение для K x ( т ) .

Для вычисления правой части (4) представим ядро Вольтерра второго порядка h ( s ₁, s ₂) первыми пятью членами ряда Тейлора в окрестности точки ( т ₁, т ₂) .

h (s1, s 2) » h (т^) +

(s,-т) 8h^’^ + (s, -т) 8h™ +.....(9)

1              1

дт ₁                     от ₂

Тогда с учетом (8):

^Kxy ^{( т} 1^{, т} 2 ) ~ ^{( A} t ⁾² • ^{[ h ( т} 1^{, т} 2 ) ⁺

(At)2 82h(т1,т2) + (At)2 d2h(т1,т2) + ] (10)

12      5т2       12      8т2

0, т >А t

h[ k, l ]«

Kх(т) =^

(1 -т). И ^А t.

Kxy (k •At, l •At) (At)^

Если один из аргументов в h ( т ₁, т ₂) равен нулю, объем пирамиды K x ( т ₁, т ₂) , учитываемый

при интегрировании, уменьшается вдвое, т.к. h ( т ₁, т ₂) = 0 при отрицательных значениях аргументов. В этом случае:

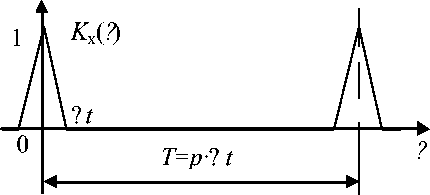
а)

б)

Рис. 2. АКФ тест-сигнала первого порядка (а) и второго порядка (б)

Ky (т, ,0)* (^• [h№ + ^• dhTT^ 2              3    от 2

(At)2 д2h(т ,0)   (At)2 д2h(т .0)    .

---2--1----2--+ -I.

12       5r,2        12      дт 22

+

2 • K „(0. l -A t )           2 • K „ ( к -A t .0)

^{h [0}- ^{1 1} *      ( a t ) 2      • ^{h [} k .⁰¹ *       (A t ) =      . (13)

В случае т , = т ₂ = 0 при интегрировании используется четверть объема пирамиды K x ( Т ] , т ₂) поэтому:

K (0,0) * (^ • [h(0,0) + A •д^00) +

xy           4                3     5т,

At 5h(0,0) (At)2 д2h(0,0)    .       (14)

---—— + -—----—— + •• I.

3    5т2       9    дт, •дт2

h [0,01 *

4 • K_X y (0,0) (A t )²

Из выражений (6, 7, 11, 13, 15) следует, что из-за отличия АКФ кусочно-постоянного тест-сигнала от δ -функции при определении ординат ИПФ и ядер Вольтерра появляется методическая погрешность. Эта погрешность для ординат h [0], h [0, l ], h [ k ,0], h [0,0] больше, чем для ординат h [ j ], h [ k , l ].

Для проверки выражений (6, 7, 11, 13, 15) выполнялось компьютерное моделирование процесса идентификации. Линейный динамический объект имитировался апериодическим звеном первого порядка, нелинейный – сепарабельным ядром Вольтера:

h1(т) = 66.6 • e -66.6т, h2(т,,т2) = 4435.56 • e-666'(т]+т 2)

программе Multisim нелинейного объекта, возбуждаемого М-последовательностью. Сепарабельное ядро Вольтерра второго порядка моделируется цепью RC и квадратором. Параметры цепи соответствуют соотношениям (16).

В процессе эксперимента при идентификации динамического объекта компьютер управляет оборудованием для генерации тест-сигнала, сбора данных. Это удобно осуществлять в специализированной среде программирования LabVIEW [5]. Автором в среде LabVIEW был создан несложный виртуальный прибор для вычисления по алгоритму (2) ординат ядер Вольтерра h [ j ] и h [ k , l ] нелинейного динамического объекта при подаче на его вход тест-сигнала на основе двоичной М-последовательности с характеристическим полиномом х ¹⁰ + х ⁹ + х ⁸ + х ⁵ + 1, Δ t = 1 мс. Динамические свойства объекта задавались соотношениями (16).

На рис. 4 приведены фрагменты лицевой панели виртуального прибора, на рисунке 5 часть блок-схемы.

В табл. 1 приведены вычисленные по выражению (16) значения ординат h , ( j • A t ) и оценки ординат h [ j ], полученные в результате моделирования процесса идентификации по выражениям (2).

В табл. 2 и 3 приведены вычисленные по выражению (16) значения ординат h ₂( к • A t , l • A t ) и оценки ординат h [ k,l ], полученные в результате моделирования процесса идентификации по выражениям (2).

В виртуальном приборе для идентификации (Рис.4) реакция объекта измеряется один раз посередине каждого такта тест-сигнала. На практике так обычно и поступают [4]. ВКФ реакции объекта и тест-сигнала вычисляется приближенно. Из табл. 1 и 3 следует, что когда время памяти исследуемого объекта в 5 ^ 10 раз превышает

На рис. 3 представлены осциллограммы входного и выходного сигналов для имитируемого в длительность такта тест-сигнала результаты удовлетворительны.

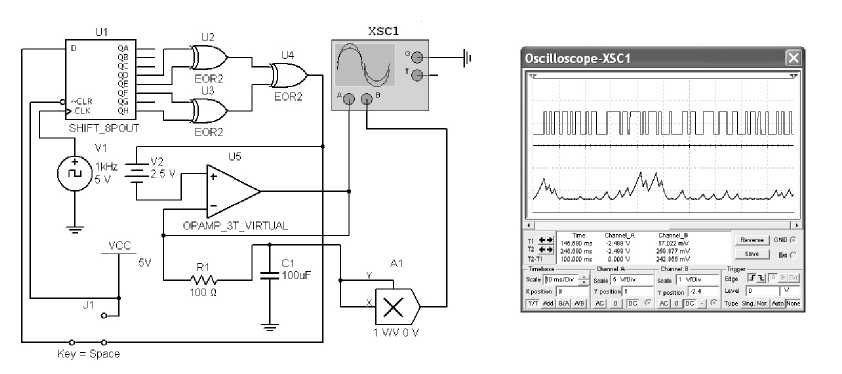
Рис. 3. Моделирование ядра Вольтерра второго порядка в программе Multisim

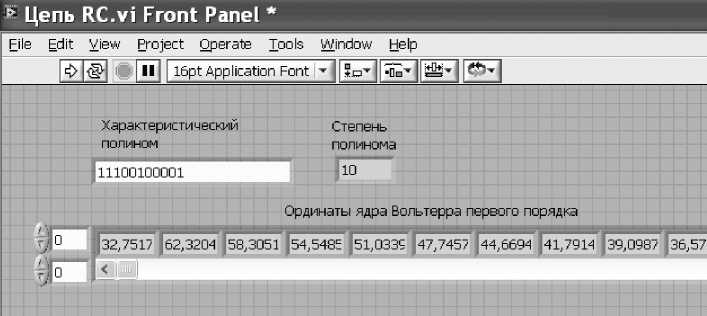
Рис. 4. Лицевая панель виртуального прибора с результатами идентификации ядра первого порядка

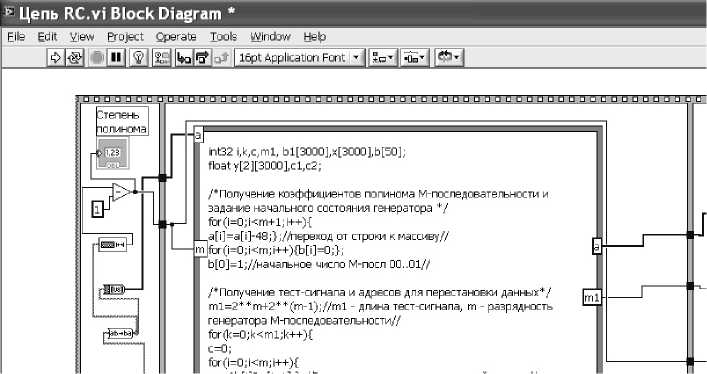
Рис. 5. Моделирование реакции объекта в блок-схеме виртуального прибора

Таблица 1. Ординаты h ₁( j ⋅ Δ t ) и оценки ординат h [ j ]

j	0	1	2	3	4	5	6	7	8
h 1 ( j ·Δ t )	66.6	62.30	58.29	54.53	51.02	47.73	44.66	41.78	39.09
h [ j ]	32.75	62.32	58.30	54.54	51.03	47.74	44.66	41.79	39.09

Таблица 2. Ординаты h ₂( k ⋅ Δ t , l ⋅ Δ t )

k, l	0	1	2	3	4	5
0	4435.5	4149.7	3882.4	3632.2	3398.2	3179.2
1	4149.7	3882.4	3632.2	3398.2	3179.2	2974.4
2	3882.4	3632.2	3398.2	3179.2	2974.4	2782.7
3	3632.2	3398.2	3179.2	2974.4	2782.7	2603.4
4	3398.2	3179.2	2974.4	2782.7	2603.4	2435.7
5	3179.2	2974.4	2782.7	2603.4	2435.7	2278.8

Таблица 3. Оценки ординат h [ k,l ]

k, l	0	1	2	3	4	5
0	1108.7	2075.1	1942.1	1815.3	1701.2	1574.6
1	2074.5	3881.3	3633.1	3396.9	3181.1	2975.2
2	1941.7	3633.7	3397.1	3178.9	2976.1	2784.1
3	1815.9	3395.9	3178.7	2973.6	2784.1	2605.2
4	1699.3	3180.1	2977.1	2783.1	2601.1	2436.3
5	1575.1	2975.4	2784.2	2601.8	2436.3	2275.8

ВЫВОДЫ

Для независимой оценки корреляционным методом ординат ядер Вольтерра или импульсной переходной функции при идентификации используют ортогональные к сдвигу кусочно-постоянные тест-сигналы малой амплитуды на основе псевдослучайных двоичных М-последова-тельностей. При этом предполагается совпадение автокорреляционной функции тест-сигнала с δ -функцией Дирака, что является упрощением.

В статье получены аналитические выражения, связывающие оценки ординат ядер Вольтера и ИПФ с соответствующими значениями взаимо-корреляционной функции тест-сигнала и реакции объекта с учетом отличия АКФ тест-сигнала от δ -функции Дирака.

Для проверки полученных выражений было выполнено компьютерное моделирование про- цесса идентификации на примере динамических звеньев первого и второго порядка.