Определение основной частоты колебании ортотропнои пластины, закрепленной в углах

(01 277).pdf (date of visit: 12.12.2012).

Прямоугольные ортотропные пластины, испытывающие динамическое воздействие в составе ракетных и космических конструкций, обладают различными способами крепления к соседним частям этих конструкций. Как правило, закрепление прямоугольной пластины осуществляется по ее краям. Края пластины могут быть жестко защемлены, шарнирно закреплены или оперты на упругие ребра.

Динамическое поведение как изотропных, так и ортотропных пластин с такими способами закрепления краев подробно изучено. Вместе с тем крепление ортотропных пластин, помимо реализуемого на краях, может осуществляться в точках. Определенный практический интерес представляет задача вычисления частот колебаний пластины, закрепленной в четырех углах. Если речь идет о нахождении нескольких частот колебаний такой пластины, то для решения этой задачи наиболее прагматичным будет использование численного метода, например метода конечных элементов. Однако определение основной частоты изгибных колебаний пластины, закрепленной в углах, может быть выполнено без привлечения методов, требующих значительных вычислительных ресурсов.

Необходимо отметить, что основная частота колебаний является удобной оценкой весовой эффективности ортотропной пластины при ее проектировании. Это обусловлено тем, что основная частота колебаний учитывает взаимное влияние изгибной жесткости и погонной массы ортотропной пластины.

Рассмотрим прямоугольную ортотропную пластину, отнесенную к системе декартовых координат xy (рис. 1). Размеры пластины по осям x и y обозначим a и b соответственно. Пластина закреплена в угловых точках таким образом, что в них отсутствует прогиб.

где T _max – максимальная кинетическая энергия движения пластины; U max – максимальная потенциальная энергия изгиба пластины. Величины T max и U max определяются следующим образом:

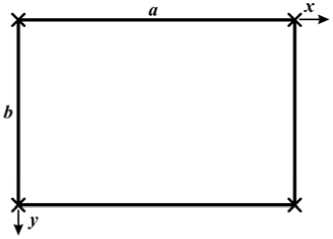
Рис. 1

ab

T max = ^Ю B p J J w ² dxdy , 2      00

ab

Umax = * f f D max 2 J J 1

ab

11 || w I + 2 D 12 V a x V

d w d w dx 2 dy 2

[ d ² w ]          [ d ² w ]

+ D       + 4 D

²² (d y ² J ³³ (d x d y J

dxdy ,

Получим вариационное уравнение изгибных колебаний пластины. Воспользуемся для этого принципом Гамильтона. Рассмотрим интеграл действия Гамильтона [1]:

t ₂

S = J (T - U ) dt , t ₁

где t – время; t 2 – t 1 интервал времени, в течение которого происходит движение пластины; T – кинетическая энергия движения пластины; U – потенциальная энергия изгиба пластины.

Кинетическая энергия и потенциальная энергия изгиба ортотропной пластины определяются следующим образом [2]:

ab

1 id w i

2^J Ц St J

2 0 0 v ^d t V

dxdy ,

ab

ab

U = 2 JJ D

_ I d ² w ] , „ d ² w d ² w

11     2   + 2 D 12    2    2 +

( d x ^{2 J} d x ² d y ²

22 22

, Id w ] Id w ] + 4 D

²² La y ² J       ³³ (a x d y J

dxdy ,

где w = w ( x , y , t ) – прогиб пластины; D ₁₁, D ₁₂, D ₂₂, D 33 – изгибные жесткости ортотропной пластины.

Рассматривая свободные колебания пластины, представим ее прогиб в следующем виде:

w ( x , y , t ) = w ( x , y ) sin ю t ,             (3)

где B_p – инерциальный параметр.

Пусть интервал времени, в течение которого рассматривается движение пластины, равен периоду колебаний. В этом случае имеет место следующее равенство:

2n t1 - t2 = .(6)

to

Подставляя (4) в (1) и учитывая соотношение (6), будем иметь

2л/

S = Tmax J COS2 /tdt - Umax J S™2 /tdt = 00

= -(T -u max max .

/

Интегрируя по времени, найдем s =-(Tmax - Umax ).                 (8)

/

В соответствии с принципом Гамильтона в промежутке времени 2π/ω, интеграл действия S для действительного движения ортотропной пластины имеет стационарное значение, т. е.

5 S = 0,                       (9)

где δ – знак вариации.

С учетом равенства (8) из условия (9) будем иметь

5 ( T max — U max ) = 0.              (10)

Подставляя (5) в (10) и выполняя варьирование, получим

ab

b

a

J J L ( x , y ) 5 wdxdy + J M_x ( x , y ) 5

^^^^^^B

J 0

где ω – круговая частота колебаний; w ( x , y ) – функция формы пластины при поперечных колебаниях.

Подставляя (3) в (2), получим

^^^^^^B

b

0 L

b

dx

J 0

^^^^^^B

T = T max coS² ® t ,

U = U max ^Sin2 ^Ю t ,                ⁽⁴⁾

^^^^^^B

^a bb

J [ / ( x , y ) ⁵ w ] ₀ dx + 2 L M xy ^{( x} , y ^{) 5} w ] ₀

a

= 0.

J 0

Здесь

О w _ /     _    \ О W

L (x, y) = Dn — + 2 ( Di2 + 2 D33) -— + dxd d w 2

+ D — B to w, 22 dy4

Mx (x, y) = D— — + D12 —,(12)

dx1

d3wd

Vx (x, У) = D11 УУТ + ( D12 + 4D33 К д 2 , 8x

22 awaw

My (x, y) = D12 -y + D22 -Г, 8x

, x       83 wd

Vy (x, У) = D11 ТГ + ( D12 + 4D33 ) уту

8x

8 ² w

M xy ^{( x} , y ) = ^{2 D} 33

п x        п y         п x . п y

5 w = sin— 5 A + sin — 5 B + sin — sin— 5 C , abab

, ( d w 1  п     п x     п     п x . п y

5I— 1 = —cos— 5 A + —cos—sin— 5 C ,    (14)

( d x )   a    a     a    a b

_J 8 w 1 п п y     n . n x п y,^

5I— 1= cos— 5 B + sin—cos— 5 C .

(d y ) b a b a b

Подставляя (14), (13) в (11), (12) и выполняя интегрирование, получим, учитывая произвольность вариаций δA, δB, δC однородную систему линейных алгебраических уравнений л4              712       4ti3 Г b1       ^

2 Du -4- A + 16 D 12 — B + — Du -y + D 12 C — a           a b a b ( a )

— B„ to-1 2 A + 16- B + 4 C | = 0, p V     п2    п )

В равенствах (12) функции M_x , M_y соответствуют изгибающим моментам, V_x , V_y соответствуют обобщенным перерезывающим силам, M_xy соответствует крутящему моменту.

Уравнение (11) представляет собой основное вариационное уравнение, которому должны удовлетворять собственные формы колебаний w ( x , y ) ортотропной пластины.

Представим прогиб пластины (рис. 2).

п             п       4 п I a 1

• 16 D12 2 2 A + 2 D12~iB+     D22 ”T + DC

• 12 a2 b2         22 b4     a2 b2 ( 22 b212

— B„to2J16A + 2B + 4C |= 0, p   (п2

4тт3 I b1       1 4тт3 Г а2

п                     п

D11 У+ D A+     D22 У+ D B+ a1 b1 ( 11 a1     11J a1 b1 ( 22 b112

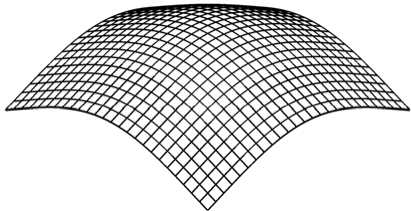
Рис. 2

п ⁴

a ² b ²

b2

D11 ” + 1 (D11 + 1D33 ) + D11 yy ab

C —

2 J 4     4

—Bp to I —A +—B + C I = 0. p (п    п)

Преобразуем уравнения (15) таким образом, чтобы коэффициенты при неизвестных A , B , C стали безразмерными. Для э того разделим каждое из уравнений (15) на D ₁₁ D ₂₂ . В результате преобразований получим

Выбранная аппроксимация

. . nx        пy        nx . пy w = A sin + B sin   + C sin   sin ,      (13)

abab где А, В и С – неизвестные числа, не удовлетворяет статическим граничным условиям на свободных краях пластины. Вместе с тем представление прогиба в виде (13) позволяет вполне успешно определить основную частоту колебаний закрепленной в углах ортотропной пластины, если для решения этой задачи использовать обобщенный метод Галеркина. Исходным уравнением для обобщенного метода Галеркина является вариационное уравнение (11). Это уравнение автоматически обеспечивает приближенное выполнение статических граничных условий на свободных краях пластины.

Вариации функции прогиба (13) и ее первых производных определяются следующим образом:

+ п ⁴

2 п ⁴ a А + 16 п 2 Р ₁₂ B + 4 п ³ ( а + в ₁₂ ) C —

(     16    4 )

— n| 1 A + -6 B + - C I = 0, V     п ¹     п )

16 п ² ₽ ₁₂ A + 1 п⁴ - B + 4 п ³ 1 ¹ + p ₁₂ | C — a (a )

—

<16        4 )

nl -6 A + 1 B + - C I= 0, (п ¹           п )

4 п ³ ( a + P ₁₂ ) A + 4 п ³

^{a + 1} ( P 12 ^{+ 2} ₽ 33 )⁺-- a

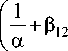
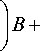
Г4    4     )

C — nl - a + - B + C I = 0. (п    п      )

Здесь

D 11 b ²           D 12              D 33

V D 11 a 2 , ^{в 12}   T d-d ;; , ^{в 33}   7 D 1 D ; ^.

Величины α, β 12 , β 33 – безразмерные геометрические и жесткостные параметры ортотропной пластины.

Величина η в уравнениях (16) определяется равенством

B to ² a ² bb n = p

D 11 D 22

Это безразмерный частотный параметр. Таким образом, задача определения основной частоты изгиб-ных колебаний ортотропной пластины, закрепленной в углах, сведена к нахождению параметра η, при котором однородная система (16) будет иметь решение, отличное от нуля.

Вычисление частотного параметра η может быть выполнено несколькими способами. Представим уравнения (16) в следующем матричном виде:

HX - nGX = 0.(18)

Здесь

H =

2 n 4 a

16 n 2 P ₁₂

16 n 2 P ₁₂

2n — a

4 n ³ ( a + P ₁₂ )

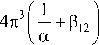
4 n 3 ( a + P ₁₂ )

V1>

4n3| - + P12 la

4I

n

П

^{a +} 2 ( P 12 ^{+ 2} Р з3 ) ^{+ —} a

Г a )

X = B

При традиционном способе величина η определяется как наименьший корень кубического уравнения, которое получено из условия det( H – η G ) = 0. В данной работе параметр η находится как наименьшее собственное число обобщенной задачи на собственные значения (18).

Из анализа коэффициентов (16) следует, что величина частотного параметра η зависит от безразмерных параметров α, β12, β33. Значения этих параметров оп- ределяются жесткостными и геометрическими характеристиками ортотропной пластины.

Когда частотный параметр η найден, основная частота колебаний может быть получена из формулы (17), т. е.

^ M D11D22 w =—. ~------, ab    Bp где ^ = 7n-

В качестве примера определим частотный параметр для изотропной пластины, толщина которой равна h. Упругими характеристиками изотропного материала являются модуль упругости E и коэффициент Пуассона ν. Плотность материала обозначим как ρ. Изгибные жесткости и инерциальный параметр для изотропной пластины определяются следующим образом:

h3

D 11 = D 22 = E 12 , D 12 = E ^V 12 ,

D12 = E X~T ?2", Bp =Ph,(19)

E где E =-.

1 -v ²

С учетом равенств (19) безразмерные параметры α, β 12 , β33 примут значения

11-v a = -, P12 =v, взз =     ,(20)

с2

где c = a/b – отношение сторон пластины.

Частота колебаний изотропной пластины определяется по формуле f =I

2 n a ² B p

Из равенств (20) следует, что частотный параметр ξ для изотропной пластины, при заданном коэффициенте Пуассона ν, зависит только от отношения c . Полагая ν = 0,3, исследуем влияние отношения сторон c , изменяющегося от 1 до 2,5, на величину частотного параметра ξ.

Приведем результаты вычисления частотного параметра c ξ для некоторых значений c (см. таблицу). В справочнике [3] можно найти аналогичные результаты, полученные с помощью метода конечных разностей. Из сравнения данных следует, что величины c ξ, найденные двумя способами, отличаются не более чем на 1,5 %. Это дает основание заключить, что предложенный в статье подход дает вполне приемлемые значения частотного параметра.

Вычисление частотного параметра

c	c ξ
1	7,22
1,5	9,05
1,0	9,10
2,5	9,49

Таким образом, с помощью обобщенного метода Галеркина решена задача определения основной частоты колебаний прямоугольной ортотропной пластины, которая закреплена от прогиба в угловых точках. Для аппроксимации прогиба пластины была использована комбинация тригонометрических функций. Показано, что рассматриваемая задача сводится к определению безразмерного частотного параметра, величина которого равна наименьшему собственному числу соответствующей однородной системы уравнений третьего порядка.

В качестве примера определен частотный коэффициент для изотропной пластины. Выполнено сравнение с результатами, полученными численным методом. Это сравнение позволило сделать вывод о том, что представленные в статье формулы позволяют с высокой точностью и минимальными вычислительными затратами определять основные частоты колебаний пластин, закрепленных углах.