Определение основной частоты колебаний прямоугольной трехслойной пластины, закрепленной в центральной точке

Важным критерием эффективности конструкции трехслойной пластины является основная частота ее колебаний. Ниже будет представлено решение задачи определения основной частоты колебаний для трехслойной пластины, закрепленной в центральной точке.

Рассмотрим прямоугольную трехслойную пластину, в центре которой расположим начало декартовой системы координат xy . Размеры пластины по осям и обозначим а и b соответственно. В центральной точке отсутствуют прогиб и углы поворота касательных к координатным линиям x и у .

Получим вариационное уравнение изгибных колебаний пластины в предположении, что линии x - 0 и у - 0 являются линиями симметрии. В этом случае можно исследовать движение только четверти пластины.

Воспользуемся для получения уравнения колебаний принципом Гамильтона:

t 2

S - J ( T - U ) dt , (1)

t 1

метр. Функции w , 0 _x и 0 _у определяют форму трехслойной пластины при изгибных колебаниях.

Подставляя (2) в (1), получим

a.^b. 17

11 1 41

0 0 LV

бе    c0v иге м  бе    два Гдеа

+d12Ы Ы Д2беx■+d22IsI    k ex      ду J V ex J V    ex      ду J V ду J

^{+ D} 33

(И  д0 у V(<0_X

I T x +   I5I П

V д у д x J V д у

(                        (диЛ

+ K j0,+— № + K K+— |5| — 1+   (3)

^x V x д x J x x V x д x J Ve x J          ⁽ )

( dw i ( dw i (dw i ?

+ К у I 0 у + — I80 у + К у 10 у +- Ы - I-®² B p w 8 w

V б у J V ^ у J Va J

Варьируя функционал (3), будем иметь

dxdy .

где S - интеграл действия Гамильтона; t - время; ( 1 ₂ — 1 1 ) — интервал времени, в течение которого происходит движение четверти пластины; Т - кинетическая энергия движения четверти пластины; U - потенциальная энергия изгиба четверти пластины: здесь T и U определяются следующим образом [1]:

J J L8wdxdy - J [ Qx8 w]^ dy - j [ Qy 8w]b dx - 0, 0 0                00

ab               b                 a

J J Lx80xdxdy - J [Mx80x ]a dy - J [Mxy80x ]q dx - 0, (4) 0 0                  00

ab               b                   a

J J Ly 80 ydxdy - J[ Mxy 80 у ] a dy - J[ Му 80 у ] 0 dx - 0, 0 0                   00

где

d ²w     d²w     d д0 ₂

L - K_x    + K_v    + K_x -x- + K_v^- + B _D ®² w ;

^x д x ^{2      у} д у ²      x д x     ^у д у    ^p

ab

^U - JJ D

0 0

T - 1 _ю ² в _pJ J w ² dxdy , ²        0 0

) "0 Y+2D

11 I _Л I ^{+ 2} D 12

V д x J

50,50     p0V

—x —^у + D ₂₂1— ^у I + д x д у      V д у J

_Т _     д w д ² 0 x д ² 0 x

Lx - - K_x ~ —+ D^ i —у + D 33 —у ^x x д x     ¹¹ д x ^{2     33} д у ²

. д²0 у

^{- K} x ⁰ x ^{+( D} 12 ^{+ D} 33 ) Д Д ^;

д x д у

-

_n |X 50 у 2

+ D₃₃ 1 — x + — - I V д у   д x J

. f _Л     д w 1        | _Л    д w j

0 ++ K 0 + xx     yy

V      д x J V      д у J

dxdy ,

Т          д w  ,           хд²0 _x

L - -K--+ (Di2 + D^3)--+ у у ду   v 12    337дxду

где w - w ( x , у ) - прогиб пластины; 0 _x -0 _x ( x , у ) , 0 _у -0 _у ( x , у ) - углы поворота нормали; D _n, D ₁₂, D ₂₁ , D ₂₂ , D ₃₃ - изгибные жесткости трехслойной пластины ( D ₁₂ - D ₂₁ ) ; K_x , К_у - сдвиговые жесткости трехслойной пластины; В _р - инерциальный пара

д ² 0_у       д ² 0_у

+ ^D33—^" + ^D 22-^- - ^Ky ⁰ у ; д x        д у

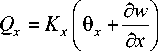
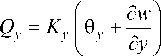
M = d | d9x xy 33 I dy

91; dx I

ДА

Mx = Di —" + D x 11              1

dx

d^

12          ;

dy

d9vd9

My = D12

dxd

.

Уравнения (4) являются основными вариационными уравнениями, которым должны удовлетворять собственные функции w ( x , y ), 9 _x ( x , y ) и 9 _y ( x , y ), от которых зависит форма действительных изгибных колебаний трехслойной пластины.

Определение основной частоты колебаний трехслойной пластины, закрепленной в центральной точке, может быть выполнено и с помощью эффективных приближенных методов, одним из которых является обобщенный метод Галеркина. В рамках этого метода прогиб w ( x , y ) и углы поворота 9 _x ( x , y ) и 9 _y ( x , y )

заменяются аналитическими выражениями, аппроксимирующими первую форму колебаний пластины вдоль осей x и y . В качестве выражений, задающих возможную первую форму пластины, закрепленной в центральной точке вдоль осей x и y , можно принять функции, полученные из решения задачи изгиба консольно закрепленной балки под действием постоянного давления.

Представим прогиб и углы поворота в следующем виде:

w = AU_x + BU _y + CU_xU_y ,

9 x = DV x + PV x U y ,             (7)

9 y = FV y + TU x V y ,

Подставив (10) в (4), после группировки получим ab                b                 a

J J LU x S Adxdy - J [ Q x U x S A ] 0 dy - J r Q y U x S A ] ₀ dx +

00                00

ab                b                  a

+ J J LU y S Bdxdy - J r Q x U y S B p y - J r Q y U y S B ] 0 dx +

00                00

abb

+J J LUxUy SCdxdy - Jr QxUxUy SC ] > - ab

- J r Q y U x U y S C ] ₀ dx = 0, 0

J JLxVxSDdxdy - J [MxVxSD]ady -000

a

• - |Г MxyVxSD ] 0 dx +JJ LxVxUySPdxdy -

• bab

• — / Г M x V x U y S P ] a dy - J r M xy V x U y S P ] ₀ dx = 0, 00

ab                b                    a

J J L , y , ^S Fdxdy - J r ^M, V y 6 F ] "dy - J r ^M , y , ^S F ] ₀ dx +

00                00

abb

+J J LyUxVyS Tdxdy - JrMxyUxVy ST ] °ody - ab

— J r M y U x V y S T ] ₀ dx = 0.

где A , B , C , D , P , F , T – неизвестные числа; U_x ( x ), V_x ( x ), U_y ( y ), V_y ( y ) – аппроксимирующие функции, которые задаются выражениями

Г,,3 „2 Al

\ x x . x , x U x ( x ) = - — ^- 4 — ⁺ 6- a a ³     a ² a

, x x ( x2 x V (x ) = x a 13a2 a

Г, ,3       „2

U y <  y ) = b by ^{- 4} 1 ^{+ 6} b

-

здесь

,

,

'A y )=b 1

y b

D

^Y x = т:7, ^y y

K x a

D 22

K y b ^{2 .}

Вариации функций прогиба и углов поворота будут иметь вид

Учитывая произвольность вариаций S A , S B , S C , S D , S P , S F , S T , получим систему из семи разрешающих уравнений обобщенного метода Галеркина с естественными граничными условиями:

ab             b               a

J J LU x dxdy - J [ Q x U x ] 0 dy - J r Q y U x ] ₀ dx = 0,

00             00

ab             b               a

J J ^LU , dxdy - J r Q x U y l 0 dy - J [ Q y U y 1 0 dx = ⁰ ,

00             00

ab             b               a

J J L x V x dxdy - J [ M x V x ] 0 dy - J r M xy V x ] 0 dx = 0 ,

00             00

ab             b          aa

J J ^L y V y ^dxdy ^- J ^r M xy V y ydly ^- J ^Г M y V y ] ₀ d^x = 0,

00             00

ab               b                 a

J J LUxUydxdy - Jr QxUxUy ^ady - Jr QyUxUy ]0 dx = 0, (12) 00               00

ab                b                   a

J J LxVxUydxdy - Jr MxVxUy ]0dy - Jr MxyVxUy ]0 dx = 0, 00                00

ab                b                    a

J J LyUxVydxdy - J[ MxyUxVy l0dy - J[ MyUxVy 10 dx = 0 , 00                00

где

S w = U_x S A + U_y S B + U_xU_y S C ,

89 _x = V_x S D + V_xU_y S P ,          (10)

S9„ = VSF + UVST .

yy xy

L = Kx

x

d ² U_x dx ²

A + K

x

d ² U_x dx ²

U y C + K y

d ² U y dy ²

B +

d 2 U

+ К—yUC+к —-d + k^up+ ydy2 xxdx xdx y dV dV

+ K_v -F- F + K_v   UT + B_o to ² AAU + + BU + CUU );

^y dy ^y dy ^{x p V x y x yl}

d ² U           dV                   dV

+K, X- UXUVC + Kx^x Up + Kx —X u2p + K, —X Up + y2 xyxyx yy y

+ K y dV^Upp + B p to ² ( AU x U y + BU y ² + CU x U y ² ) dxdy

L = -KdUxA-KdUxU C + Dud-VxD + xx      xy dx dxdx d2Vd

+ DMIP + D₃₃ y V_XP - KVD -

11 dx 2 y 33 dy 2 xxx

- KxUyVxP+ (D12 + D33) dVydUxT; dy dx dU      dU

L y = - K y-p B - K y -pUx C + ( D 12 + D 33 ) x dy        dy

■ J ^[ K_XDVU_X + K_XPVU_X ² + KAdU x U, + KCdU x, 0 L ^{x x y x x y x} dx ^{y x} dx

a

U y

- 0

dy -

a

- J K y FV y U y + K y TU x V y U y + K y B

0 L

dU

+ K yC-Xy U x U y dy

dU

U y + dy

1 1 dx = 0;

- 0

dU             2            d2V x У.,' P + D33--2xVyT + D22

dy dx dx ²             dy ²

d 2 V

+ D 22 -rfUx T - K y V y F - K y V y U x T ; dy ²

ab

U K

00 L

d ² U            d ² U            d ² U

—x^uuAL + к —x^uUup + к —^yLuup? + dx ^{2 yxx}dx ^{2 yxy}dy ^{2 yx}

a = К ^f DV + PVU + Ad— x + CdU x U, ) ;

x     x (   x x y      dx       dx   yJ f             dU    dU)

Qy = Ky\FVy + TUxVy + B + '^

(                 dy      dy f dUdU

M = D33\P-rVx + T--xVy I;(14)

^ dy dx

_d 2 _U

+Kv--^UUC + Kx^xUvUxD + К —x-U2UxP + ydy2 xyxdx yxxdx yx dV          dV

+Ky -pUyUxF + Ky -Xu^xUyT + Bpto2 x dy             dy x (Auxuy + Buxuy + CU2Uy )1 dxdy -

b

■ I" K_xDVHH_v + KPVUU 22 + K_XA xxxy xxxy x

0 -

a x UxUy + KxC-UxUxU^y dx       J0

dU

--x x dx

dy -

dV dV        dV dV

Mx = D,,D— + D.P^U, + D12F— + DT^U ; x11              11           y12              12           x dx dx           dy dy

J

■ J K y FV y U x U y + K y TU x V y U y + K y B

0 L

dU y

--— x dy

dV dV        dV dV

Mv = Di2D— + DnP—U + D22F— + DP—UX. y 12             12          y22             22          x dx dx           dy dy

dU x UxUy + KyC—^uxUy dy

b dx = 0;

- 0

С учетом (14) разрешающая система уравнений примет вид

J J ^[ K_x d-U^U.A + K_x d—UyUUC + K_y dU-Up +

^J 0^J₀ L x dx ² x x dx ^{2 y} x ^y dy ²     x

+ к d-U y U_x ² C + K_xVUD + pdV x U U_XP + Кd u F + ^y dy ^{2   xx} dx ^{x x} dx ^{yx y}dy ^x

J J ^[ - К dU x V A - К dU x V_XU C + D! d-Vx V_XD +

J J L x dx x x dx x y 11 dx2 x d2V            d2U

+ D ll— x-UVP + D 33-- ^V²P - KV²D -

11 dx 2 yx 33 dy 2 x xx

- K_XUP²P + ( D ₁₂ + D₃₃)^— xv T xyx 12   33 dy dx x

dxdy -

+ K^dV^U 2 T + B_n to² ( AU 2 + BU_XU_V + CU 2 u J dxdy ^У dy x P \ x x ^y x ^y J X

-I

^J [     dF       dF

J D 11 D-V x V x + D 11 P-V x U y V x + D 1₂ F

0 L      dx          dx

dV       dV    1 ^J

'-y Vx + D12T-yUxVx dy dy          dy     J0

- J ^[ KDVU + KPVUV + OdU-U + KCdU x UU xxxxxyxx  xx  xy

1 ^J.

dy -

- 0

a

-

dU^y J D 33 P^L 0 L dy

V 2 + DuTdU x VV x 33 dx yx

b

dx = 0;

^- 0

a

-Ux        -Ux

-f К FV U + KTUX + KB Xu + KC y-U2 0 L y y x y x y y dy x y dy x ab

»K

00 L

1 ¹ dx = 0 ,

- 0

^{J J [}- K x dU^V_xU y A - K x dUxV^ ^ C + D , 00 L dx              dx

d ² V

' 11— 2xX V x U y D ⁺ dx

d ² U         d ² U          d ² U

X--fUM +Kx--tU2 C + Kv--5yUyB + xdx 2yxdx 2yydy 2y

d ² V            d ² U

+ D_n— xX U^Vp + D₃₃-- У V 2 UP - KV 2 U_VD - 11 dx 2   y x 33 dy 2 xy xxy

-Vv

- K x U y V x P + ( D 12 + D 33 )- y--x V x U y T -x-y y x J

_

тое и седьмое – на величину 315 a D ₁₁ D ₂₂ . Тогда

однородная СЛАУ в матричном виде запишется как

b

"J DuD . V , + D-P- x

₀ L dx              dx

UV + yx

HZ = O ,                  (16)

dV          dV

+ D_nF^^VU + D₁₂T—^yU_xV_xU_v

12 dy xy 12 dy xxy

j Г     -Uv x         dU

-J D 33 P—^ V x² U y + D 33 T-U x V y V x U y

0 L       -y               -x

a

^-y ^-

- 0

1 b

, -x = 0;

- 0

где Z – матрица неизвестных; H – матрица, элементы которой имеют следующий вид:

ab ii - Ky

0 0 _

dU       dU

V y B - K y -pU x V y C + ( D 12 + D 33 )x dy          dy

,      1°8aЛ          1         ,252

^h 11 =-- ( Y 2 x ⁺ 35 Y px ) ⁺ 8 nY 1 x , ^h 12 =—n? 0 x Y 0 y ,

Y x V               ’ h16 = 0 , h17 = 0 ,

,      «Y0y (216_ hi3 =--1—Y2x + 1512Ypx | + —nY0yY1 x,

Y x I 5

dU               ²             d ² V

--y —^V_vP + D₃₃--.xV 2 T + D₂₂ y-VF + dy dx ^{y 33    2 y 22    2 y}

h 21

d ² V y

⁺ D 22---7"

²² dy ²

U x V y T - K y V y F - K y V y U x T -x-y

-

b Г      -U_v           du„ ,

-J D 33 P ; V V + D 33 T-U x V 2

0 L       -y              -x

-y -

- 0

h 14 = ^{- 315} — Y 3 x , ^h 15 = ^{- 126} — Y 0 y Y 3 x , Y _x                 Y _x

252                108

= —nY 0 x Y 0 y , h 22 =-- ( Y 2 y ⁺ 35 Y py ) ⁺ 8 nY 1 y ,

5                     aY y x h24 = 0, h25 = 0,

,        Yov 1216       _ r. - I 16

h 23 =--1— Y 2 y + 1512Y py l + — nY 0 x Y1 y , aY y к 5               J 5

- j Г D^DdV x V + D_nPdV x 0 L ¹² -x ^{y 12} -x

U y V y +

dV        dV

+ DxxF — V_v + D.J   UV

22 dy y 22 dy xy

b

-x = 0; J 0

h 26 ⁼

-

— Y 3 y , h =- — Y 0 x Y 3 y , aY y          ^a

aY

^a Y0 y 1216     ...-

----1 ^Y 2 x ^{+ 1512} Y px

Y x I ⁵

y

I 16

J ⁺ у nY 0 y Y 1 x ,

ab ii - Ky

0 0 _

dU        dU

--y VUB -K yU2 VC + (Dn + D33) x dy yxydy xy12  33

Y_Ox | 216                I 16

--1— Y 2 y ^{+ 1512} Y py l + — nY 0 x Y 1 y , aY _y к 5                J 5

dU                 ²               d ² V

-7-"V^VyUxP + D33 : VU T + D2-TTVyUxF+ dy dx              dx2              dy2

1       nr aY1 У I Y2x h33 =-96—- -^x + y„v

³³          Y x 1 35 ^px

nr ^Ylx I ^Y 2 y        I ¹⁶

96—1x- ^ + y   +---nYixYiv, py               1x 1y aYy ( 35 J 315

⁺ D ²² л ' dy

- ² V „            ,             „     "

f -V y T - K y V y2 U x F - K VU x T -x-y

h - ata aY3x м    и - eaY3x h34 = 126 Y0y , h35 =8 Y1 y , Yx                  Yx

-

1   — iic ^Y 3 у »

h36 = -126     Y0x , aY y

- 8 23 У - ,_L , . ^a Y y

Ь -Uv            dU x

-[ D 33 P— + D 33 T—-V2Ux

^{J 33} -y ^{x y x 33} -x ^{y x}

1 ^{0 -}y ^-

^- 0

h         aY3 x h           _ nz; aY3 x h41 = 315      , h42 = 0, h43 = 126      Y0 y ,

Y _x                          Y _x

a

-J D 12 D-V-V y U x + D 12 P-V-U y V y U x +

₀ L -x             -x

h 44 =- 15 -( 7 y x + 3 ) , Y _x

dV          dV

+ D^F — VvUx + D 22 T—UX VV

22 dy yx 22 dy xy

b

-x = 0.

- 0

aYov Г h45    6 3      I 2yx + -l, h46 =-3 5P12,

V 1         /

Y _x

Выполнив в уравнениях (15) интегрирование, после некоторых преобразований получим однородную систему линейных алгебранческих уравнений (СЛАУ), которую приведем в удобный для анализа безразмерный вид, для чего умножим первые три уравнения на величину 315ab D11D22 , четвертое и пятое уравнения – на величину 315b D11D22 , а шес-

aYov   , л h47 = -105312Y3x , h51 = 126      Y3x , h52 = 0,

h 53 = 8       ^Y 3 x , h 54 =

Y _x

^a Y 0 y

Y _x

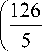
h 55

^a Y 1 y 1 8     4

--- -Yx +-

Y x к 5 x 7

^- P 33

f 54

^-^ y 2 y + 270 y py J ,

h 56 =- 105 P 12 Y 3 y ,

h57 =-315 (p!2 Y3x Y3y +Рзз Y3x Y3y ) , h6! = 0, h62 =-315 ?", h63 =-126 -^^, aYy              ayy h64 =-35p12, h65 =-105p!2Y3y, h66

1 («    315

--I 63yy +---- aYyI   y 14 .

h 67 = -—⁽ 126 Y y + 9 1 , h 71 = 0, h 72 =- 126 "'" x^ , aY y I 5 J                       aY y

1        e Y1 x Y3у h73 =-8------ , aY y h74 = -105P12Y3x , h75 = -315 (P12Y3x Y3y + в33 Y3x Y3y ) ,

Yox (126

h76 =- —1— Y y + 9 I , aYyI 5

h 77 = -₽ 33 1 - Y 2 x + 270 Y px        1 - Y y + - I .

V 7             J aY y V 57

Безразмерные комплексы

Y o x = 3 + 20 y x , Y o y = 3 + 20 y y ,

Y 1 x = 91 + 999 Y x + 3024 y 2 , Y px = 3 + 12 y x ,

Y 1 y = 91 + 999 Y y + 3024 Y y , Y 2 x = - 5 + 2- Y x + 560 Y 2 ,

Y 2 y = ^{- 5 +} 28 Y y ^{+ 560} Y У ,

18      18     612

• ^Y 3 x = 7 ⁺ 5 ^Y x , ^Y 3 y = 7 ⁺ 5 ^Y y , ^Y 3 x = 7 ⁺ ""5" ^Y x ,

Y 3 y = 7 ⁺ у Y y , Y py = ³ + ¹² Y y ,        ⁽¹⁸⁾

D 11          D 22        b ² D 11

^Y x K x a 2 , ^Y y K y b 2 , a 2 ND 22

В = D 12 В = D 33

• ¹²      D 11 D 22 , ³³     D 11 D 22

и безразмерный частотный параметр

Bою2 a2bь n= 1      -

D ₁₁ D ₂₂

определяются только жесткостными и геометрическими характеристиками материалов несущих слоев и заполнителя трехслойной пластины.

Таким образом, задача определения основной частоты изгибных колебаний трехслойной пластины, закрепленной в центре, сведена к нахождению безразмерного частотного параметра n , который вычисляется как наименьший вещественный корень кубического уравнения det ( X ) = 0, полученного из условия существования нетривиального решения однородной СЛАУ (16).

Когда частотный параметр n найден, то основная частота колебаний может быть получена из формулы (19) с учетом равенств а = а] 2 и b = b /2 :

⁴Уп / У D 11 D 22 аЬ ^   B р

В качестве примера определим основную частоту колебаний для нескольких трехслойных пластин, закрепленных в центральной точке и отличающихся размерами в плане, толщинами несущих слоев и заполнителя. Несущие слои выполнены из материала со следующими параметрами: E xt ) = 54,55 ГПа, E yt ) = = 54,55 ГПа, G ( t ) = 20,67 ГПа, G ( t ) = 3,78 ГПа, G ( t ) = xy                      xz                     yz

= 3,78 ГПа, v⁽ _y t ’ = 0,32, v ⁽J’ = 0,32, р, = 1 500 кг/м³. xy                yx               t

Материал заполнителя характеризуется модулями сдвига G^_x h ) = 440 МПа, G yh ) = 220 МПа и плотностью р _h = 83 кг/м3. Пластины имеют размеры в плане: b = 1 м, a = 1 и 2 м. Суммарная толщина несущих слоев t равна 0,001 и 0,002 м, а толщина заполнителя 8 будет 0,01; 0,05; 0,1 м.

Частоты колебаний трехслойных пластин, вычисленные по формуле (20) для указанных выше размеров, приведены в табл. 1.

Для проверки полученных результатов определим основную частоту колебаний трехслойной пластины, закрепленной в центральной точке, методом конечных элементов (МКЭ). Расчет выполним в пакете COSMOS/M, используя конечный элемент SHELL4L [2]. Значения частот, вычисленных с помощью МКЭ, приведены в табл. 2.

Таблица 1

Частоты колебаний трехслойной пластины, закрепленной в центральной точке, Гц

t , м	a = 1 м, b = 1 м			a = 2 м, b = 1 м
	δ = 0.01 м	δ = 0,05 м	δ = 0,1 м	δ = 0,01 м	δ = 0,05 м	δ = 0,1 м
0,001	50,186	153,72	230,01	15,052	46,428	70,067
0,002	57,961	193,36	298,73	17,408	58,877	92,508

Таблица 2

Частоты колебаний трехслойной пластины, закрепленной в центральной точке, Гц, полученные МКЭ

t , м	a = 1 м, b = 1 м			a = 2 м, b = 1 м
	δ = 0,01 м	δ = 0,05 м	δ = 0,1 м	δ = 0,01 м	δ = 0,05 м	δ = 0,1 м
0,001	49,221	149,19	223,70	14,592	45,880	68,051
0,002	56,868	189,31	290,56	16,925	57,961	67,123

Сравнивая соответствующие частоты из табл. 1 и 2, можно сделать вывод, что разница не превышает 5 %. Таким образом, определение основной частоты колебаний трехслойной пластины, закрепленной в центральной точке, может быть достоверно выполнено обобщенным методом Галеркина.

Таким образом, с помощью обобщенного метода Галеркина решена задача определения основной частоты колебаний прямоугольной трехслойной пластины, которая закреплена от прогиба и углов поворота в центральной точке. Данная задача сводится к нахождению безразмерного частотного параметра, который является наименьшим вещественным корнем кубического уравнения.

Сравнение полученной формулы с решением, выполненным методом конечных элементов, показывает, что данная формула обеспечивает высокую точность и минимальные вычислительные затраты при определении основных частот колебаний пластин, закрепленных в центральной точке.