Определение основной частоты колебаний прямоугольной трехслойной пластины с двумя свободными краями

При проектировании трехслойных пластин часто возникает задача выбора геометрических и упругих параметров, которые обеспечивают максимальную изгибную жесткость и минимальную погонную массу конструкции [1; 2]. Особенностью этой задачи является взаимное влияние изгибной жесткости и погонной массы трехслойной пластины. Это влияние проявляется в том, что рост из-гибной жесткости пластины всегда сопровождается увеличением ее погонной массы. Поэтому для проектирования трехслойных пластин необходим определенный критерий эффективности конструкции. В качестве такого критерия удобно использовать основную частоту колебаний трехслойной пластины.

Рассмотрим прямоугольную трехслойную пластину, которая состоит из двух одинаковых композитных несущих слоев и ортотропного заполнителя. Введем систему декартовых координат xyz , связанную со срединной плоскостью пластины. Обозначим размеры пластины по осям x и y через a и b соответственно. Пусть края пластины x = 0 и y = 0 будутжестко закреплены, а края пластины x = a и y = b свободны.

Получим вариационное уравнение изгибных колебаний трехслойной пластины, используя принцип Гамильтона. В соответствии с этим принципом, интеграл действия Гамильтона для действительного движения трехслойной пластины в некотором промежутке времени имеет стационарное значение. Выберем в качестве этого промежутка период колебаний с круговой частотой ω . Тогда условие стационарности интеграла действия Гамильтона примет вид

δ ( T max - U max ) = 0, (1) где δ – знак вариации; T _max – максимальная кинетическая энергия трехслойной пластины; U _max – максимальная потенциальная энергия изгиба трехслойной пластины. Величины T _max и U _max определяются следующими выражениями:

1 ab

T _max = ω ² B _ρ ∫ ∫ w ² dxdy ,

2 00

22 ⎛∂w⎞⎛∂w⎞ +K  θ+ +Kθ+ xx     yy

⎝∂ x ⎠⎝∂ y ⎠

dxdy ,

где w = w ( x , y ) – прогиб пластины; θ _x =θ _x ( x , y ) , θ _y =θ _y ( x , y ) – углы поворота нормали; D ₁₁, D ₁₂, D ₂₁, D ₂₂ , D ₃₃ – изгибные жесткости трехслойной пластины ( D ₁₂ = D ₂₁ ) ; K _x , K _y – сдвиговые жесткости трехслойной пластины; B _ρ – инерциальный параметр. Функции w , θ _x и θ _y определяют форму трехслойной пластины при изгибных колебаниях.

Подставим (2) в (1):

ab _⎡⎛ ∫∫ ⎢⎜ D 1 00 ⎢⎣⎝

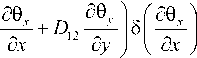
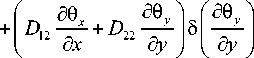
⎛∂θ ∂θ y ⎞⎛∂θ ⎞ + D ₃₃ ⎜ ^x + ^y ⎟δ⎜ ^x ⎟+ ⎝∂ y ∂ x ⎠⎝∂ y ⎠

ab

U max

⎛∂θ ⎞2       ∂θ ∂θ x+2Dxy +

11                      12

⎝∂ x ⎠        ∂ x ∂ y

ab = ¹ ∫∫ ⎢ D 1

А А

+ D ₂₂

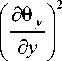
+ D ₃₃

∂θ ∂θ xy

∂ y ∂ x

+

+ D ₃₃

∂θ ⎞⎛∂θ ⎞

^{∂θ x} + ^y ⎟δ⎜ ^y ⎟+ K_x ^⎛⎜θ _x +^{∂ w ⎞}⎟δθ _x + ∂ x ⎠⎝∂ x ⎠⎝∂ x ⎠

∂ y

+ K x ⎜θ x

∂ w ⎞⎛∂ w ⎞⎛∂ w ⎞

+ δ + K θ+ δθ+ ⎟⎜⎟ y ⎜ y ⎟ y

+ K y ⎜θ

∂ w ⎞⎛∂ w ⎞

+    ⎟δ⎜     ⎟-ω ² B w ∂ w

∂ y ⎠⎝∂ y ⎠^ρ

dxdy .

Варьируя функционал (3), получим

∫a ∫b Lδwdxdy -∫b [θxδw]0ady - ∫a ⎡⎣θyδw⎤⎦bdx =0, 00             00

ab              ba

∫∫ L x δθ x dxdy - ∫ [ M x δθ x ] ₀ ^ady - ∫ ⎡_⎣ M xy δθ x ⎤_⎦ ^b ₀ dx = 0,

00              00

ab               ba

∫∫ L y δθ y dxdy - ∫ ⎡_⎣ M xy δθ y ⎤_{⎦ 0} ^ady - ∫ ⎡_⎣ M y δθ y ⎤_⎦ ^b ₀ dx = 0, (4)

00               00

где ²² ∂θ ∂θ

L = K_x ^{∂ w} ₂ + K _y ^{∂ w} ₂ + K _x ^x + K _y ^y + B ω ² w , ^x ∂ x ^{2 y} ∂ y ^{2 x} ∂ x^y ∂ y ^ρ ,

L=-K∂w +D xx    112

∂x∂

+D33    2x -Kxθx+(D11+D33)y ,(5)

∂y 2

L =- K ^{∂ w} + ( D + D ) ^{∂ 2 θ x} + ^yy ∂ y ^{12  33} ∂ x ∂ y

∂ ² θ        ∂ ² θ

+ D ^y + D ^y

³³ ∂ x ^{2      22} ∂ y ²

-

K y θ y ;

;

∂θ

M = D ^x + D x 11              12

∂ x

∂θ y _;

∂ y ^;

M y

⎛∂θ

M = D ^x xy 33    _∂ y

∂θ ^x D 12

∂ x

∂θ y ⎞

. ∂ x ⎠

∂θ y

²² ∂ y ,

Представим прогиб и углы поворота в следующем виде:

w = FU x ( x ) U y ( y ) , θ x = T x V x ( x ) U y ( y ) , θ y = T y U x ( x ) V y ( y ) , у ,              (12)

где F , T_x , T_y – неизвестные числа; U_x ( x ), V_x ( x ), U_y ( y ), V_y ( y ) – аппроксимирующие функции, которые задаются выражениями

U x ( x ) = ^x a

x x x ⎛ x ₃ - 4₂ + 6 - 12 γ _x ⎜- 2

aa^a ⎝ ^a

Здесь Q_x , Q_y – перерезывающие силы, M_x , бающие моменты, M_xy – крутящий момент.

M _y – изги-

V ( x ) = ^{x ⎛ x 2} - ^x x 2 a ⎝ 3 a   a

Уравнения (4) являются основными вариационными уравнениями, которым должны удовлетворять собственные функции w ( x , y ), θ _x ( x , y )и θ _y ( x , y ),влияющие на форму действительных изгибных колебаний трехслойной

U y ( y ) = _b ^y

32 ^{y 3} - 4 ^{y 2} + 6 ^y - 12 γ b 3 b 2 b

y

b

пластины.

Полученные вариационные уравнения могут быть использованы для формирования традиционной краевой задачи определения основной частоты колебаний рассматриваемой трехслойной пластины. В силу произвольности вариаций δ w , δθ _x , δθ _y подынтегральные выражения в двойных интегралах дадутуравнения движения

2 V ( y ) = ^{y ⎛ y y ()} b ^⎜⎝ 3 b ²

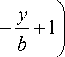
пластины:

L =0, Lx =0, Ly =0.

Подынтегральные выражения в одинарных интегралах зададут естественные граничные условия на краях x = 0, x = a :

Qxδw=0, Mxδθx=0, Mxyδθy =0, и на краях y=0, y=b:

Qyδw=0, Mxyδθx=0, Myδθy=0.

Для рассматриваемого нами закрепления трехслойной пластины граничные условия (8) и (9) примут следующий вид:

x = 0, w= 0, θx =0, θy =0, y=0, w=0, θx=0, θy=0,         (10)

x=a, Qx =0, Mx =0, Mxy = 0, y=b, Qy =0, My =0, Mxy =0.        (11)

Точное определение частот и форм колебаний исследуемой трехслойной пластины связано с решением однородной краевой задачи (7), (10) и (11), которое вызывает значительные математические затруднения и не получено до настоящего времени. Однако определение основной частоты колебаний данной пластины может быть выполнено с помощью весьма эффективных приближенных методов, одним из которых является обобщенный метод Галеркина. В этом методе прогиб w ( x , y )иуглы поворота θ _x ( x , y ), θ _y ( x , y )заменяются аналитическими выражениями, которые аппроксимируют первую форму колебаний пластины вдоль осей x и y . В качестве функций, задающих возможную первую форму таких колебаний, можно принять функции, полученные из решения задачи изгиба консольно закрепленной балки под действием постоянного давления.

Здесь

^D 11             D 22

^γ x       ^, γ= .

^K x ^{a 2     y} K y b ²

Безразмерные параметры γ _x и γ _y

характеризуют

сдвиговые податливости трехслойной пластины в плос-

костях xz и yz соответственно.

Производные отаппроксимирующих функций (13) и (14) могутбыть найдены по следующим формулам:

dU y ₌ 4 dy b

32 ^y - 3 ^y + 3 ^y - 6 γ b ³ b ² b

dV ⎛2        ⎞ y =1 ⎜y2 -2 y+1⎟, dy   b ⎝b2    b ⎠

y b

-

dU	32 ⎡⎤
x dx a	⎢ x 3 - 3 x 2 + 3 x - 6 γ x ⎛⎜ x - 1 ⎞ ⎣ aaa   ⎝ a ⎠⎦	,
dV 1 ⎛ xx ⎞
x =⎜ 2 + 1. dx a ⎝ a    a ⎠		(17)

Вариации функций (12) имеютвид

δ w = U x U y δ F , δθ x = V x U y δ T x , δθ y = U x V y δ T y . (18) Подставляя (12) и (18) в соотношения (4), (5), (6) и учитывая произвольность вариаций δ F , δ T_x и δ T_y , получим ab                b                  a

∫∫LUxUydxdy-∫⎡⎣QxUxUy⎤⎦0ady-∫⎡⎣QyUxUy⎤⎦b0dx=0, 00                 00

ab                ba

∫∫LxVxUydxdy-∫⎡⎣MxVxUy⎤⎦0ady-∫⎡⎣MxyVxUy⎤⎦0dx=0, (19) 00                 00

ab                b                   a

LUVdxdy -⎡ MUV ⎤ ^ady -⎡ MUV ⎤ dx = 0, yxy      ⎣ xyxy ⎦ ₀ ⎣ yxy ⎦ ₀

00                 0                     0

где

⎛ L =⎜ K x

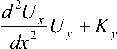
d ² U y dx ²

U ⎟ F + K ^x UT + xxyx x ⎟ x dx yx

dV

+ K y^y U x T y + B ρ ω ² U x U y F = 0, dx

dU f    d2 V           d 2 U,

L, =-K, "UF + 1 Di fU, + D»Vx -KVU, Iх xx     y    11     y33 xxxy dx I dx               dy)

хT +(D12 + D33) dUx dVy T _ 0, x12     33 dx dy y dUdU

L =- KU---F + (Dn + D 3) -V-y yyxdy 12  33 dx dy x f   d2 U          d2 V)

+ D₃₃--xVy_v + D_nU--y- - KU_XV, T = 0;

( ³³ dx ^{2 y 22} x dy ² y x y J ^y

Q _ K fV T + dUxF) U, x xxxy

^ dx )

dVdV

Mx = Dll— UTx + DyjUx—Tv;

x 11        yx 12 xy dxdy f dUv )

y

Qy     y          dyJ dVdV

My = D12 "V^UTx + D22Ux    T;(22)

dxdy f dU dU )

Mxy = D33 V ^T + ^yVyTy .(23)

xy 33 ( x dy x dx y y)’

Уравнения (19) автоматически обеспечивают приближенное (интегральное) удовлетворение граничных условий (11) на свободных краях пластины.

Выполняя в уравнениях (19) интегрирование, получим следующую однородную систему линейных алгебраических уравнений:

[ Kx ( I 2 x - Px ) 11 y + KyI1 x ( I 2 y - Py )]x хF + Kx (13x — Sx ) 11 yTx +

+ K y I 1 x ( 1 3 y - S y ) T y + B p ® 2 1 1 x I 1 y F = 0,    ⁽²⁴⁾

- K x J 3 x I 1 y F +

+ [ D 11 ( J 2 x - R x ) 1 1 y + D 33 J 1 x ( I 2 y - P y ) - K x J 1 x I 1 y ] T x +

+ [ D 12 ( J 3 x - S x ) 1 3 y + D 33 J 3 x ( 1 3 y - S y ) ] T y = 0,

- K y J 3 y I 1 x F +

+ [ D 22 ( J 2 y - R y ) 1 1 x + D 33 J 1 y ( 1 2 x - P x ) - K y J 1 y I 1 x ] T y +

+ ^[ D ( J - S „) I _3x + D₃₃ J_{3 v} ( I _3x - S , ) 1 T = 0, ₁₂ 3 yy 3 x  333 y 3 xxx

S x = [ U x V x ] a ,

S y =^[ U y V y ] b .

Определим значения интегралов (25), используя (13), (14), (16) и(17):

8aa

1 1 x "  315 ^Y 1 x , J 1 x "  14,

I " 8 b=

1 y 315 Y1 y, 1 y 14, 12

I 2 x            Y 2 x, J 2 x

35a5

=-Jl_v    J =-_1

2y      35b Y 2y,   2y

I =Y3 x _T _ 6 Y3 x

3x 35 , 3x35 ,

I _Y 3 y      _ 6 Y 3 y

3y    35 , 3y35 ,

где

Y 1 x = 91 + 999 Y x + 3024 y 2 , Y 2 x " - 5 + 28 y x + 560 y 2 ,

Y3x = 5 + 56Yx, Y3x = 5 + 14Yx,(

Y 1 y = 91 + 999 y y + 3024 Y 2 , Y 2 y " - 5 + 28 Y y + 560 Y 2 ,

Y3y = 5 + 56yy, Y3y = 5 + 14Yy.(29)

Определим значения величин P , R , S , P , R , x x xy y

S _y , входящих в коэффициенты уравнений системы (24). Учитывая равенства (24), (25) и (26), соотношения (26) можно представить в следующем виде:

Px "  — (1 + Yx), R = 0, S x = 1 + Yx, xxx  x  x

a

^P y "  1 b ² ( 1 + Y y ) , R y "  0, S y "  ¹ + Y y .       (30)

Подставляя (30) в (24), после некоторых преобразований имеем где

ab

1 1 x = J Ux² dx , 1 1 y = J U y dy ,

( K x I 2 x I 1 y + K y I 1 x I 2 y ) F - K x J 3 x I 1 y T x -- K y I 1 x J 3 y T y + B p ® 2 1 1 x I 1 y F "  0,

a

J 1 x = J V x² dx , 0

i ₂x " kdU ^, 2 x ₀ x dx 2

a 2

J lx =    --- Г -x ,

2 x ₀ x dx 2

dV

I lx = U x dx , 3 xx dx

b

J1 y = J Vy dy, b   d2Uy

I2'"iU'^ dy• b   d2Vy

^J2 y •     ^v d    dy',

I „-X - p -. , ^dy

^J 3 x "  J ^V x dU ' ^,ld , ₀ dx

^b dU _y

^{J 3} y "^{J V}■^^-, '^,

- K x J 3 x I 1 y F + ( D 11 J 2 x I 1 y + D 33 J 1 x I 2 y - K x J 1 x I 1 y ) T x

^{-( D} 12 I 3 x I 3 y ^{- D} 33 ^J 3 x^J 3 y ) ^Ty "  ⁰,

^K y ^J 3 y I 1 x ^{F (} D 12 I 3 x I 3 y ^D 33 ^J 3 x ^J 3 y ) ^T x ⁺

⁺ ( ^D 33 ^J 1 y I ^{2 x + D} 22 ^J 2 y I 1 x ^{- K} y ^J 1 y I 1 x ) ^T y "  ⁰, где

7       ^24y 2 x   7 _ ^{24 y 2} y           (32)

I 2 x _-- , I 2 y "-- ,            ⁽³2)

здесь

Y 2 x "  15 + 84 y x + 280 Y 2 ,

γ 2 y = 15 + 84 γ y + 280 γ ² y .             (33)

Преобразуем уравнения (31) таким образом, чтобы коэффициенты при неизвестных стали безразмерными. Для этого подставим соотношения (27) и (32) в систему (31), а затем умножим каждое уравнение на величину 99225 ab /V D ₁₁ D ₂₂ . В результате преобразований получим

1728 a ₁₁ F + 432 a ₁₂ F_x + 432 a ₁₃ F_y = 64 b ₁₁ η F ,

432 a ₂₁ F + 36 a ₂₂ F_x + 81 a ₂₃ F_y = 0,        (34)

432a31F+81a32Fx+36a33Fy=0, где

F x = aT x , F y = bT y .               (35)

Коэффициенты a_{i , j} ( i , j = 1, 2, 3) имеют следующие значения:

Частотный параметр η зависитот безразмерных параметров α, β12, β33, γx, γy, значения которых определяются жесткостными и геометрическими характеристиками трехслойной пластины с композитными несущи- ми слоями и ортотропным заполнителем.

Основная частота колебаний щ этой пластины при известном параметре η определяется по равенству (38):

λ ω=

,

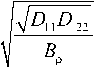
где λ=vη .

В качестве примера определим основную частоту колебаний для нескольких трехслойных пластин с двумя свободными краями, отличающихся размерами в плане, толщинами несущих слоев и заполнителя. Пусть несу- a11= α

γ 2 x γ 1 y γ _x

1 γ 1 x γ 2 y + , αγ _y

1 γ 1 x γ 3 y αγ _y

3x 1y a22= α       +135β33γ2y,

γ _x

+ 135 β ₃₃ γ _{2 x} ,             (₃₆)

1 γ 1 x γ 3 y a 13 ⁼ a 31 ⁼

αγ _y

γ 1 y γ 3 x a ₁₂ = a ₂₁ =α , γ _x

a 23 ⁼ a 32 ^{= β} 12 γ 3 x γ 3 y ⁺ 36 γ 3 x γ 3 y , b 11 ⁼ γ 1 x γ 1 y , где α , β ₁₂, β ₃₃ – безразмерные параметры:

α=

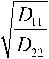
¹ 12 ⁼

^β 33 ⁼

Величина η , входящая в первое уравнение системы

(34), является безразмерным частотным параметром: B _ρ ω ² a ² b ² η= ^ρ

Таким образом, задача об определении основной частоты колебаний рассматриваемой трехслойной пластины сведена к вычислению безразмерного параметра η , при котором однородная система уравнений (34) будет

иметь решение, отличное от нуля.

Получим формулу для параметра η . Используя второе и третье уравнения системы (34), исключим из первого уравнения неизвестные F_x и F_y . Затем, учитывая, что F ≠ 0, получим для η следующее выражение:

щие слои выполнены из материала со следующими параметрами: Ex(t)=54,55ГПа, Ey(t)=54,55ГПа, Gx(ty)=20,67ГПа, Gx(tz)=3,78ГПа, Gy(tz)=3,78ГПа,ν(xty)=0,32, ν(ytx)=0,32, ρt = 1 500 кг/м3. Материал заполнителя характеризуется модулями сдвига Gx(zh)=440МПа, Gy(zh)=220МПаиплот-ностью ρh = 83 кг/м3. Рассмотрим пластины со следующими размерами в плане: b =1м,a = 1 и 2 м. Пусть суммарная толщина несущих слоев t равна 0,001 и 0,002 м, а толщина заполнителя h будет0,01; 0,05; 0,1 м. Безразмерный параметр η определяется с помощью формул (34), (38), (39). Для вычисления круговой частоты колебаний ω используется уравнение (40). Частоты колебаний f =ω/2π трехслойных пластин с различными значения ми размеров а, tи h приведены в табл. 1.

Для проверки полученных результатов определим основную частоту колебаний трехслойной пластины c двумя свободными краями с помощью метода конечных элементов. Расчет выполним в пакете COSMOS/M. Для моделирования воспользуемся конечным элементом SHELL4L. Значения частот колебаний, вычисленных с помощью метода конечных элементов, представлены в табл. 2.

Сравнивая соответствующие частоты из табл. 1 и 2, можно сделать вывод, что разница между полученными результатами не превышает 5 %. Это дает основания утверждать, что определение основной частоты колебаний трехслойной пластины c двумя свободными краями мо-жетбыть достоверно выполнено с помощью предложенного в данной статье способа.

η= ⎢ a ₁₁ + 27 b ⎢

9 a ₁₂ a ₁₃ a ₂₃ - 2 ( a ₂₂ a ₁ ² ₃ + a ₃₃ a ₁ ² ₂

16 a ₂₂ a ₃₃ - 81 a ₂ ² ₃

. (39)

Таким образом, было получено решение задачи об определении основной частоты колебаний трехслойной

Таблица 1

Частоты колебаний трехслойной пластины c двумя свободными краями

t ,м	a = 1м			a = 2м
	h = 0,01 м	h = 0,05 м	h = 0,1 м	h = 0,01 м	h = 0,05 м	h = 0,1 м
0,001	30,759	93,808	139,648	19,084	58,426	87,377
0,002	35,492	117,428	179,770	22,038	73,458	113,415

Таблица 2

Частоты колебаний трехслойной пластины c двумя свободными краями (МКЭ-решение)

t,м a = 1м a = 2м h = 0,01 м h = 0,05 м h = 0,1 м h = 0,01 м h = 0,05 м h = 0,1 м 0,001 30,057 90,811 134,722 18,692 57,169 85,203 0,002 34,402 113,229 171,913 21,555 71,766 110,381 пластины, у которой два смежных края жестко закреплены, а два других свободны. Пластина состоит из двух одинаковых композитных несущих слоев и ортотропного заполнителя. Для решения динамической задачи был применен обобщенный метод Галеркина.

Выведена формула для определения основной частоты колебаний трехслойной пластины c двумя свободными краями. Верификация этой формулы для пластин с различными жесткостными параметрами выполнена с помощью метода конечных элементов. Сравнение между собой результатов вычислений позволило сделать вывод о пригодности выведенной в статье формулы для надежного и быстрого определения основной частоты колебаний трехслойной пластины c двумя свободными краями.