Определение основной частоты колебаний прямоугольной трехслойной пластины со свободным краем

Исследование изгибных колебаний трехслойных пластин является важным этапом их проектирования. Трехслойные пластины, совершающие изгибные колебания, обладают самыми разнообразными способами закрепления краев. К настоящему времени большинство решений задач об определении частот колебаний трехслойных пластин получены для случая, когда все четыре края шарнирно закреплены. Большой практический интерес пред- ставляет задача динамического анализа трехслойной пластины, в которой один из ее краев свободен, а три других жестко закреплены. Для трехслойных пластин рассматриваемая задача не имеет до настоящего времени своего решения. Такая ситуация обусловлена трудно стями выбора функций, аппроксимирующих форму пластины в рамках моделей, учитывающих особенности движения трехслойной структуры. Вместе с тем из общей задачи определения спектра частот колебаний трехслойной пластины можно выделить одну частную задачу, решение которой можно получить в компактном виде. Речь идет о задаче вычисления основной частоты колебаний трехслойной пластины с рассматриваемыми граничными условиями. В настоящей статье решена задача определения основной частоты колебаний трехслойной пластины со свободным краем, которая состоит из двух одинаковых композитных несущих слоев и ортотропного заполнителя. Вариационные уравнения движения пластины были получены с помощью принципа Гамильтона. Решение этих уравнений было выполнено методом Канторовича и обобщенным методом Галеркина.

Рассмотрим прямоугольную трехслойную пластину, состоящую из двух одинаковых композитных слоев и ортотропного заполнителя. Отнесем срединную плоскость пластины к декартовым координатам ху . Размеры пластины по осям х и у обозначим а и b соответственно. Край пластины при у = b свободен, а остальные три края ( у = 0, х = 0, х = a ) жестко закреплены.

Получим вариационное уравнение поперечных колебаний трехслойной пластины. Рассмотрим интеграл действия Гамильтона

5 = РЫт, (1) J т гдет - время; т2 -т1 - интервал времени, на котором происходит движение пластины; L – функция Лагранжа. Числовые значения функционала S зависят от подынтегральной функции L, которая определяется следующим равенством:

L = T - U ,                 (2)

где T и U, соответственно, кинетическая энергия и потен- циальная энергия изгиба трехслойной пластины, совер- шающей поперечные колебания. Кинетическая энергия и потенциальная энергия изгиба трехслойной пластины равна [1]:

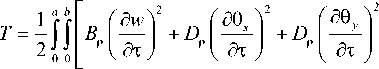
dxdy ; (3)

ab

U = 1И

(89 )2

D,, — + 2 D,2

^5x J

( d6 Y

+ D 22 1       I

I ^d y J

7           _ _ X 2

, (56, 56 y )

I +1

( d x d y J

+ Kx 6

x

где w = w ( x , y , т ) - прогиб пластины; 6 _x = 6 _x ( x , y , т ), 6 _y = 6 _y ( x , y , т ) - углы поворота нормали к срединной плоскости; D 11 , D ₁₂ ( D ₁₂ = D ₂₁), D ₂₂, D ₃₃ - изгибные жесткости трехслойной пластины; K_x , K_y – сдвиговые жесткости трехслойной пластины; B _р - инерциальный параметр; D _р - параметр, обусловленный инерцией поворота.

Рассматривая свободные колебания трехслойной пластины, представим прогиб w и углы поворота 6 _x , 6 y в следующем виде:

w ( x , y , т ) = w ( x , y ) sin ют ,

⁶ x ( ^x , y , ^т ) = ⁶ x ( ^x , y ) ^{sin ют} ,

6y (x, y, т) = 6y (x, y) sin ют, (5) где ю - круговая частота колебаний; w(x, y), 6x (x, y), 6y (x, y) - двумерные функции, определяющие форму трехслойной пластины при поперечных колеба- ниях.

Подставляя уравнения (5) в равенства (3) и (4), полу- чим следующее:

T = T max cos^{2 ют} , U = U max sin^{2 Ют} ,        ⁽⁶⁾

где Tmax – максимальная кинетическая энергия пластины; Umax – максимальная потенциальная энергия изгиба пластины. Величины Tmax и Umax определяются следую- щими выражениями:

T max

ab

= -ю²[ f( B_pw² + D _p6„²

J J \ ^{р р x}

²    00

ab

U = -ff max

D № ¹¹1 d x ,

⁺ D 22

+ D p 6 y ² ) dxdy , 56 x d6 y +

I2    _

J + 2 D ,2

Y

y

I ⁺ 33 5 y J

d x d y

(56 ^ ₊ 56 y ? ( d x d y J

( 6w i             6w

+KI6.+— I + K 6 +— x I x dx J     y ( y dy J dxdy,

где w = w ( x , y ) , ⁶ x = ⁶ x ( x , y ) , ⁶ y =⁶ y ( x , y ) .

Подставляя выражения (2) и (6) в равенство (1), получим

• ⁵ = 1^ ( T max cos^{2 Ют-} U max sin^{2 Ют} ) d ^       ⁽⁸⁾

Будем рассматривать движение пластины за один период колебаний. Тогда т2 -т, = 2п/ю.                    (9)

С учетом соотношения (9) равенство (8) примет следующий вид:

2п / ю                            2 п / ю

5 = T _max f     cos² ют d т- U_max       sin² ют d т . ⁽¹⁰⁾

max ₀ max ₀

Выполняя интегрирование по времени, найдем

5 =- ( T max - U max ) -              (11)

ю

В соответствии с принципом Гамильтона, интеграл действия (11) для действительного движения трехслойной пластины в промежутке времени 2 п / ю имеет стационарное значение. Тогда

5 5 = 0,                     (12)

где 5 - знак вариации.

Принимая во внимание равенство (11), из уравнения (12) будем иметь следующее:

5 ( T max - U max ) = 0.                 (13)

Подставляя выражение (7) в формулу (13), получим ab ff I D„    + D

^J o ^J o Ц ¹¹ d x      ¹

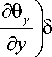
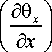
, d6 x

¹² d x

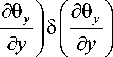
⁺ D 33

⁺ D 33

<59, 59 y Wd9, I — x_ ₊ — y 151 — x (5 y d x J ( d y

59  ^d9 y Lf⁵⁹ y ) v L  ⁵ w)

— + —- ⁸ —- + Kx 9_X +— 59 + 5%     5% I Sx

5 y

+ K

x

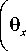
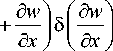
+ K y

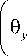
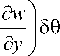
y

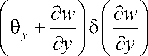
-m 2 ( B „ w 5 w + D p 9 x 59 x + D p 9 y 59 y ) ] dxdy = 0. (14)

Уравнение (14) представляет собой основное вариационное уравнение, которому должны удовлетворять собственные формы действительных поперечных колебаний трехслойной пластины. Получим решение этой задачи с помощью метода Канторовича и обобщенного метода Галеркина [2; 3].

На защемленных краях пластины x = 0 и x = a реализу-

ются следующие граничные условия:

w _ 0, 9 _x = 0, 9 y = 0.              (15)

Метод Канторовича позволяет понизить размерность вариационного уравнения (14), если прогиб w и углы поворота 9 _x , 9 y представить в следующем виде:

^w ( ^x , y ) = ^w ( y ) U x ( ^x ) ,

⁹ x ( ^x , y ) = ⁹ x ( y ) V x ( ^x ) ,              (16)

⁹ y ⁽ x , y ^{) = 9} y ⁽ y ) V x ⁽ x ) , где w ( y ) , 9 x ( y ) , ⁹ y ( ^y ) – неизвестные функции, аппроксимирующие форму пластины вдоль оси y ; U_x ( x ) , V x ( x ) -известные функции, аппроксимирующие форму пластины вдоль оси x . Функции U_x ( x ) и V_x ( x ) имеют следующий вид:

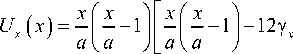
x I x 2 xX -I

V x ^{( x ) =} -| 2 — ^- 3- ^{+ 1} I ,            (17)

a ( a a J               ^{v 7}

где

Y x = D„ /Ka ².                 (18)

Безразмерный параметр γ _x характеризует сдвиговую податливость трехслойной пластины в направлении оси x . Из равенств (17) следует, что на краях пластины x = 0 и x = a функции U_x и V_x равны нулю. Поэтому выбранная аппроксимация прогиба и углов поворота (16) удовлетворяет граничным условиям (15).

Подставляя выражения (16) в формулу (14) и интегрируя результат по x , получим следующее одномерное ва-

риационное уравнение:

b

J{ K x ( J 3 x 9 x + 1 2 x w ) 5 w + K y i , x

.   dw L[ dw

9 y +|5| y dy J ( dy

d 9„

+ ( D 11 J 2 x + K x J 1 x ) 9 x + K x J 3 x w + D 12 1 3 x-?y 59 x + dy

_ I T d 9 x   T _Q W d 9 x

⁺ D 33 I J 1 x      + J 3 x ⁹ y |⁵|

V     dy        JI dy

( D 33 1 2 x + K y i 1 x ) 9 y + K y i 1 x dy + D 33 J 3 x -y 59 y -

-

d6 J f d 9„

D12I3 " ■ D22Iix— 5 — 123xx221x dy J ( dy

-m ² ( B p 1 1 x w 5 w + D p J 1 x 9 x 59 x + D p 1 1 x 9 y 59 y ) } dy = 0, (19)

где w = w ( y ) , ⁹ x =⁹ x ( y ) , ⁹ y =⁹ y ( y ) .

В уравнении (19) a                      a ²

I , x = J U x dx , 1 2 x = J | dU x I dx ,

0               0 V dx J

^I 3 x

= f UdV^dx , J

₀ ^x dx ¹

= J V xx dx , 0

т   a f dV |\    _T f_vdUx,

^J 2 x = J / dx ^{, J} 3 x = J V x      ^dx .       (20)

Ь V dx J             0 dx            ^v '

Подставляя выражения (17) в уравнения (20), полу-

чим

I = a Y 1 x I = 2 Y 2 x I _ Y 3 x ^{1 x} 630^{, 2 x} 105 a ^{, 3 x} 105^,

J, _ a— J_x _ — J _^^ x^ ^{1 x} 210^{, 2 x} 5 a ^{, 3 x} 105

где

Y 1 x _ 1 + 108y x + 3 024 Y 2 ,

Y 2 x _ 1 + 84y x + 2 520 Y 2 , Y 3 x _ ¹ + ⁴² Y x . (22)

Выполним далее операцию варьирования функционала (19). В результате преобразований, учитывая равенства (21), получим следующее:

ЬI               d^w                  d 9„I

[ KxIixw-KIix^ + KxJy9x -KIix— - Bom2Ixw x x 2 x          y 1 x               x 3 x x y 1 xp

J, (                  dy2                        dyJ

x5 wdy +

^:y I 1 x |9 y

dw L — |5 w dy J

_ 0;

b

[ Г KJw + (DJ.+ KJ J9.- xxxxxx

-D J d ^{9 x} +(£) I -D J ) d ^{9 y} - 33 J 1 x dy 2 X 12^J3 x ^33 J 3 x ) dy

- D m ² J . .9,159, dy + p 1 x x I x *

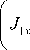
d9x-+J j dy    3xy

b

_ 0; (23)

^] 0

b ^Г KyI\xdw + ( D 33 J 3 X- D I2 I 3 x) d ^ x y 1 x 33 3 x 123 x

0, L        dy                       dy

(                              d ² 9

+ ( D 33 1 2 x + K y i 1 x ) 9 y - D 22 1 1 x-"5y -

- D p m ² 1 1 x 9 y ]59 y dy +

d 9„]

D 12 I 3 x9.+ D 22 I X— 59„

12 3 xx 22 1 xy dy J

_ 0.

При традиционном подходе к решению задачи об определении основной частоты колебаний трехслойной пластины из соотношений (23) в силу произвольности вариаций 5 w , 59 _x , 59 _y можно получить разрешающие дифференциальные уравнения движения вдоль оси y :

Kxi2xw - KyI1 x     + KxJ3x6x - dy2

d "?

- K y i 1 x-p - B p ® ² 1 1 x ^ = 0;

dy

KxJ3 xw + ( D11J2 x + KxJ1 x )6 x - d 26 x ,                 dd 6 y        2

D 33 J 1 x , 2 ⁺ ( D 12 I 3 x D 33 ^J 3 x ) ,     D p ® J 1 x ⁶ x = 0;

dy 2

где

V y ⁽ У ) = y

У ² - У

3 b ² b

Y у = D 22/ K y b 2 .

Kyi1 x^ + (D33 J3x - D1213x ) d6 + dydy d 2 6        2

+ (D3312x + Kyi1 x )6y - D2211       - Dp®211 x6y = 0, dy2

и естественные граничные условия на краях y = 0 и y = b :

K y i 1 x [o y + dw J 5 w = o, I dy J

D 33 | J 1 x p ⁺ J 3 x ⁶ y |⁵⁶ x = ⁰,

I dy J

f

I D12i3x6x + D22i 1       I 56y = 0.(25)

I

Для случая, когда край y = 0 жестко закреплен, а край y = b свободен, граничные условия (25) примут вид

У = 0, w = 0, 6x = 0, 6y = 0,(26)

f„

У = ⁰ , ^Kyⁱ 1 x l ⁶ y +-7- I = ⁰

I dy)

D33 I J1 xd6- + J3x6y | = 0, I dy J d 6V

D 12 i 3 x 6 x + D 22 i 1        = 0.            (27)

dy

Безразмерный параметр γ _y характеризует сдвиговую податливость трехслойной пластины в направлении y .

Вариации функций, определяемых равенствами (28), имеют вид

5 w = U y 5 F , 56 x = U y 5 T x , 56 y = V y 5 T y .     (31)

Подставляя равенства (28) и (31) в выражения (23), получим, учитывая произвольность вариаций 5 F , 5 T x и 5 T_y , разрешающие уравнения обобщенного метода Галеркина:

b

J

x 2 x

-

-

d ² Uy |

I ---y F + y 1 x dy2 J dV

K y i 1 x-pT y - B p ® ² i 1 x U y F dy

X

b

^x U y dy ^+[ R ( y ) ] 0 = ⁰;

[ j KJ^UyF + ( D! J ₂,+ KJ. ) u„ x 3 xy     11 2 xx 1 xy

d ² U y

^- D 33 ^J 1 x  , 2

dy ²

,                   X dVy _ I

+ ( D,213 x - D33 J3 x )         Dp®2 J-xUT |X xUydy+[ Rx ( у )] 0 =0;

0 f dUy ,              у dUy

Ki "F^ F + (D33 J^x - Di2i3 x ) ^T + yxxxx о I       dy                       dy

+ ( D 33 i 2 x + K y i 1 x ) V y

-

d ² V

D22I1x     y dy2

T x +

T - D ю ² i , У

Уравнения (27) означают, что на краю y = b обращаются в ноль перерезывающая сила, крутящий момент и изгибающий момент.

Рассматриваемая задача определения первой частоты колебаний может быть решена с помощью обобщенного метода Галеркина [3]. Для реализации этого метода необходимо воспользоваться уравнениями (23). В соответствии с основной идеей метода Галеркина заменим функции w ( y ) , 6 _x ( y ) и 6 ( y ) приближенными аналитическими выражениями, которые достоверно аппроксимируют первую форму колебаний трехслойной пластины вдоль оси y . В качестве таких аппроксимирующих функций можно принять функции, полученные при решении задачи об изгибе консольно закрепленной балки под действием постоянной нагрузки [4]. Представим w ( У ) , 6 x ( y ) , 6 y ( y ) в следующем виде:

^w ( У ) = FU y ( У ) , ⁶ x ( У ) = T x U y ( У ) ,

⁶ y ( У ) = ^Ty^Vy ( У ) , (28) где F , T x , T - неизвестные числа; U_y ( y ) , V_y ( y ) -аппроксимирующие функции, определяемые выражениями

x V y dy + [ R y ( y ) ] b = 0

где

/ X I       dUy |

R ( У ) = K yⁱ 1 x | V y T y + ^ "^ F J U y ,

, X f dUy             |

R x ( у ) = D 33 1 J 1 xpp T x + J 3 x V y T y I U y ,

I dy            J

, у I                         dV_y |

R y ( У ) = I D 12 i 3 x U y T x + D 22 i 1 x^ y y T y I V y .    (33)

При y = 0, U _y = 0 и V _y = 0. Тогда из равенств (28) следует, что w ( 0 ) = 0 , 6 x ( 0 ) = 0, 6 _y ( 0 ) = 0 . Таким образом, выбранная аппроксимация (28) и (29) удовлетворяет граничным условиям (26) на защемленном краю трехслойной пластины. При y = b для функций U_y и V_y и их первых производных справедливы следующие равенства:

U y = 3 ( 1 + 4 y y ) , V y = 1/3, dUy /dy = 4/ 1 , dVy /dy = 0.

Uy I y ) =У

y ³ b ³

-

4 4 + 6 У - 12y _b 2 _b

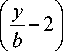
Подставляя равенства (28) при y = b в левые части уравнений (27) и учитывая формулы (34), получим три не равные нулю выражения:

K y i 1 x I 3 T y + -F \* 0, D 33 ^f-

3 J 3 x T y P 0,

3 D 12 1 3 x T x ( 1 + 4y y ) * 0.               (35)

Подразумевается, что в общем случае F * 0, T x * 0, T_y * 0. Из выражений (35) следует, что выбранная аппроксимация (28) и (29) не удовлетворяет традиционным граничным условиям (27) на свободном краю трехслойной пластины. Однако обобщенный метод Галеркина не требует обязательного точного удовлетворения функциями U_y и V_y граничных условий на свободном краю пластины. Уравнения (32) автоматически обеспечивают приближенное выполнение граничных условий при y = b .

Величины [ ^{R (} y ) ] 0 , [ R x ⁽ y ) ] 0 , [ R y ^{( y} ) ] ₀, входящие в уравнения (32), могут быть представлены в следующем виде:

[ R ( У ) ] ^b = R ( b ) - R ( 0 ) , [ R x ( У ) ] 0 = R x ( b ) - R x ( 0 ) ,

[ R y ( У ) ] 0 b = R y ( ⁰ ) - R y ( ⁰ ) .           (36)

Подставляя y = b в уравнения (33) и учитывая, что U_y = 0 и V_y = 0 , получим R ( 0 ) = 0 , R x ( 0 ) = 0 и R y ( ⁰ ) = 0.

Тогда из формул (36) будем иметь:

[ R ( y ) ] 0 b = ^R ( b ) , [ ^Rx ( y ) ] 0 = ^Rx ( b ) ,

^[ R y ⁽ y ) ] 0 = R y ^{( 0} ) .                 (37)

Выполним в уравнениях (32) операцию интегрирования по y . В результате преобразований, учитывая равенства (37), получим

( K x I 2 x I 1 y - K y I 1 x I 2 y ) F + K x J 3 x I 1 y T x —

• - K y I i x I 3 y T y — B ® 1 1 x I 1 y F + R ( 0 ) = 0,

K x J 3 x I 1 y F + [ ( D 11 J 2 x + K x J 1 x ) 1 1 y - D 33 J 1 x I 2 y ] T x +

+ ( ^D 12 I 3 x - ^D 33 ^J 3 x ) I 3 y^Ty - ^D p ® ^{2 J} 1 x I 1 y^Ty + ^Rx ( ⁰ ) = ⁰, (38)

K y I 1 x J 3 y F + ( D 33 J 3 x - D 12 1 3 x ) J 3 y T x +

+ [ ( D 33 1 2 x + K y I 1 x ) J 1 y - D 22 1 1 x J 2 y ] T y -

-Dp®211 xJ1 yTy + Ry (0) = 0, где b             b   d2Ub

I1 y I Uyd, I2 y =J Uy—^y, I. y 1 U^*, 0                 0y0

^{b            b} d ² V

J1 y = J Vy dy, J2y = JVy —dy, J3y = J Vy -r-dy. (39) 0              0     dy

Подставляя выражения (29) в формулы (39), найдем

8 b 1 y 315 Y 1 y ,	I 2 y	- 12       I =23 ,, 35 0 72y , 3 y 35,
b J 1 y 14,	J 2 y =	- X J = A" 5 0 ’ 3y 35 Y 3 y ,	(40)

где

Y 1 y = 91 + 999 y y + 3 024 у 2 , у 2 y = - 5 + 28 y y + 560 y 2 ,

Y3y = 5 + 56yy, Y3y = 5 + 14yy.(41)

Определим значения величин R ( 0 ) , R_x ( 0 ) , R_y ( 0 ) , входящих в уравнения (38). Полагая в уравнениях (33) y = b и учитывая равенства (34), будем иметь следующее:

^R ( ⁰ ) = ~ (¹ + 4Y y ) K y I 1 x^F + ( ¹ + ⁴ Y y ) K y I 1 x T y ,

R x ( 0 ) = 2 ( 1 + 4y y ) D 33 J 1 x T x + ( 1 + 4y y ) D 33 J 3 x T y , (42) R y ( 0 ) = ( 1 + 4y y ) D 12 J 3 x T x .

Подставляя выражения (42) в уравнения (38), получим однородную систему линейных алгебраических урав-

( K x I 2 x I 1 y - K x I 1 x" 1 2 y ) F + K x J 3 x I 1 y T x -

- K y I 1 x" 1 2 y T y - B p ® 2 1 1 x I 1 y F = 0,

K x J 3 x I 1 y F + [ ( D 11 J 2 x + K x J 1 x ) 1 1 y - D 33 J 1 x I 2 y ] T x +

+ ( D 12 1 3 x I 3 y - D 33 J 3 x" 1 3 y ) T y - D p ® 2 J 1 x I 1 y T x = 0, (43)

K y I 1 x^J 3 y^F + ( ^D 33 ^J 3 x^J 3 y - D 12 I 3 x^J 3 y ) ^Tx +

+ [ ( D 33 1 2 x + K y I 1 x ) J 1 y - D 22 1 1 x J 2 y ] T y - D p ® 2 1 1 x J 1 y T y = 0, где

I 2 ^y = I 2 y - ¹^ I ¹ + 4r y ) , I 3 y = 1 3 y - ( 1 + 4y y ) ,

J3y = J3y -(1 + 4Yy ).

Учитывая выражения (40) и (41), преобразуем равенства (44) к виду

I 2 y =-350 У 2 y , 13 y =-J3 y , J 3 y =-13 y ,(45)

где

Y 2 y = 15 + 84y y + 280y y.(46)

Приведем уравнения (43) к уравнениям с безразмерными коэффициентами. Для этого подставим равенства (40), (45) в формулы (43) и затем умножим каждое уравнение на величину396900ab/ D11D22 . В результате преобразований получим a11 F + a12Fx + a13 Fy -n011F = 0, a21F + a22Fx + a23Fy - n022F = 0,         (47)

a31F + a32 Fx + a33 Fy -n033F = 0, где

F x = aT x , F y = 0T y .

Коэффициенты системы равны a11 = 48 4a

Y 2 x Y 1 y + 9 У1Л2 Y x     ^a  Y y

,

an = 481 a Y3xY1 y + 27P33y2., I, I   Y x          J a 33 = 9

Y 1 x Y 3. ^aY y

^{+ 60} ₽ 33 Y 2 x ,

Y 3 x Y 1 y a₁₂ = a ₂₁ = 96a------,

Y x_

_    _ 108 Y1 x Y3y a13    a 31                    ,

a   Y y a23 = a32 = 108y3x (6в33 y3y - P12Y3y ) , 011 = 16Y1 xY1 y , 022 = 48 rx Y1 y , 033 = 45 ry Y1 x .

В равенствах (49) введены следующие обозначения:

a =

^D 12

¹² V DD ’

^D 33

_{D 11 D 22}   (50)

X DDDD, w =—, ---- ab

B р

,

Dp       Dp r =--— r =-— x Bp a2 y   Bp b2

где

Величина П , входящая в уравнения (47) и определяемая равенством

п =

B _рю ² a ² b ²

^D 11 ^D 22

,

является безразмерным частотным параметром.

Таким образом, задача определения основной частоты колебаний рассматриваемой трехслойной пластины сведена к вычислению параметра п , при котором однородная система (47) будет иметь нетривиальное решение. Приравняем к нулю определитель системы (47), т. е.

^a 11

det <

^-п ^b 11

^a 21

^a 31

^a 12

a

a

П b 22

^a 13

U 0.

П Ь зз

Из условия (5з), учитывая, что а ₁₂ = а ₂₁, а _1з = а _з1, а _2з = а _з2, получим характеристический полином третьей степени

X = Vn- (59)

Получим формулы для вычисления изгибных жесткостей D_mn ( mn = 11,12,22, зз ) , сдвиговых жесткостей K_x , K y и инерциальных параметров B _p , D _p . Рассмотрим структуру трехслойной пластины. Пусть суммарная толщина несущих слоев равна t , а толщина заполнителя равна h . Материал несущих слоев характеризуется коэффи-циентамижесткости A^ ) ( mn = 11,12, 22, зз ) , трансверсальными модулями сдвига G xz ) , G yz ) и плотностью p t . Аналогичные характеристики заполнителя обозначим A mn ) ( mn = ^11,12,22,33 ) , G h ) , G y- ) , p - .

В рамках сдвиговой теории, используемой в настоящей работе для описания движения трехслойной пластины, изгибные и сдвиговые жесткости, а также инерциальные параметры могут быть определены по следующим формулам:

Dmn

= A * „^Z■ , ( mn = 11,12, 22, зз ) ,

где

H 3 П ³ - H 2 П + H 1 П- H 0 = 0,

^H з    ^b 11 ^Ь 22 ^Ь зз ,

H 2 = ^а _п b 22 ^b зз ⁺ a 22 ^b 11 ^b зз ⁺ a зз ^b 11 ^b 22 , H 1 = ^b _n ( a 22 a зз ^- a 22з ) ⁺

где

⁺ b 22 ⁽ a 11 a зз

-

« 123 ) ⁺ b зз ( a ll a 22

^{- а} 22 ) ,

-

^{- а} 1²з ^а 22

-

_a 2 _a

-

2 ^a 12 ^a 33 ^.

Уравнение (54) имеет три вещественных корня. Наименьший из этих корней будет определять требуемый частотный параметр п .

Если не учитывать инерцию поворота, то для вычисления параметра п можно получить простую формулу. Пусть D _Р = 0. Тогда из формул (51) следует, что r x = 0 и r y = 0. В этом случае коэффициенты b ₂₂ и b _зз обратятся в ноль, и из уравнений (55) будем иметь следующее:

H _з = 0, H ₂ = 0, H 1 = b 11 ( а ₂₂ а _зз - а 2 _з ) . (56)

Подставляя равенства (56) в уравнение (54), получим

K x

^B Р

Z xz

Z yz

G x ) t Z xz , = p t t Z P ,	K y = G yz ) t Z yz , t 3 d p   P 1 12 Zp ,	(61) (62)
( h )    3 mn Z mn Z+ J( t ) .з , Amn t		(63)
hh 2 Z = 1 + з — + з — :-, t t 2		(64)
+ - 1 t J	i,    -G Z t ) Y1 xz <    tG Zz h )    ’ xz
p+ - Y 1 t J	( t )        1 1+ - G y^ 1 1     tG yz !) J ’	(65)

; , = 1+^ - , s ,^ . p t t               p t t

П = ^H 0 / H 1 .

Величина частотного параметра з, определяемого из уравнения (54) или с помощью формулы (57), зависит от безразмерных параметров у _x , у y , a , P ₁₂, Р _зз, r x , r_y , которые содержат всю информацию о жесткостных, геометрических и инерциальных характеристиках трехслойной пластины с композитными несущими слоями и ортотропным заполнителем.

При известном частотном параметре п основная частота колебаний трехслойной пластины может быть получена из равенства (52) и представлена в следующем виде:

Получим расчетные формулы для параметров у _x , у y , a , Р ₁₂, Р _зз, r x , r y . Подставляя формулы (60), (61) в выражения (18) и (30), будем иметь следующее:

( t )       2                                    ( t )       2

v =   A11-1    1^1- v = — A22_I _ |522_ x 1 2g(t) I a2 k , y 1 2g(t) 162 k . (67) xz              xz                    yz             yz

Из равенств (50) с учетом соотношения (60) получим

a =

Р зз =

b ² , P 12 a ²

( t )

^A 33

( t )

⁷¹12 Z 12

A 1t 4 1EXV ^ зз

V A ,⁰? A 22 ) _x- -

Подставляя равенства (62) в формулы (51), найдем

1 t2 Zp           1 t2 Z, r =--Z7 — . r =--; '

x 12 а ² Z y 12 b ² Z ^p

1 p

p

.

Формула для частоты колебаний (58) с учетом равенства (60) и первого из равенств (62) примет следующий вид:

го = X

2. i p m ⁾ A 2) VCHiH" ab 2ТИ   P -   \ ^ZP

В трехслойных пластинах часто используется так называемый легкий заполнитель, обладающий малой жесткостью в плоскости xy . Для такой структуры можно принять AmУ ) = 0 ( mn = 11,12, 22, 33 ) . Тогда из формулы (63) следует, что C _mn = C ( mn = 11,12, 22, 33 ) . В этом случае равенства (67) и (68) примут следующий вид:

Выражение для частоты колебаний следует из равенства (73), т е.

. 1 1    №x ' E у^{- 1}

го = Х---------- —.           (75)

ab 1V3 V    P -     \ ^z p

1 A i) f t ² ) i

Y =--— — —. Y,,

^Y x 12 G^ ) I a ² Jz^ , y xz              xz

A 2) f tL Li_ = 12 G^{( 1} ) I b² J Z , yz             yz

_o_ №b‘    - A '2’ и = A 33’

“A A 2 ¹ a     = A A              A ■

Пусть материал несущих слоев обладает следующими параметрами: E X¹ ) = 54,551 ГПа, E y¹ ) = 54,551 ГПа, G xy ’ = 20,668 ГПа, х^ = 0,319 7, v£ = 0,319 7, G xz ) = 3,779 ГПа, Gy'_z ) = 3,779 ГПа, p _t = 1 500 кг/м ³ . Материал заполнителя имеет G ^z¹ ) = 440 МПа, G yh ) = 220 МПа p_h = 83 кг/м ³ . Пусть размеры пластины в плане принимают следующие значения: b = 1 м, a = 1, 3, 5 м. Толщина несущих слоев 1 = 0,001 м, а толщина заполнителя h = 0,01; 0,05; 0,1 м. Для

Параметры r_x и r y остаются без изменений.

Подставляя в формулу (70) C_n = C ₂₂ = i , получим для определения основной частоты колебаний трехслойной

пластины с легким заполнителем следующее выражение:

t 1 ГО = Х--;=, ab 2V3 V

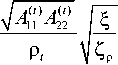
Как уже отмечалось, задача определения основной частоты колебаний трехслойной пластины со свободным краем не имеет решения до настоящего времени. Поэтому для верификации полученных в статье формул выполним сравнение вычисленных с их помощью частот с частотами, найденными методом конечных элементов.

Рассмотрим пластину с ортотропными несущими слоями и легким ортотропным заполнителем. Для такой пластины расчетные формулы (72), (71), (69) примут следующий вид:

a =

—( - )   ,

E             P,

E У ) a²

F ⁽ t )V - )                  G⁽¹ )

^{x V} xy R =----- xy---- ^{( 1         1} )                                 ^{( 1         1} )

E x E y          E ^x E ^y

,

—( 1 ) / о \

1 E x f 1 ² ) C

Y = x 12 Gx) ( a2 Jz xz

1 t2 ip r =

x

¹² a ^Z P

Y y

( - )

1 E y f -2_ ^J_

12 G ^{( 1} ) I b² J Z , yz             yz

1 1 ² c

Г =--;--'

^y 12 b ² Z

1P

.

P

пластины с рассмотренными выше характеристиками найдем частоту колебаний f = го / 2 п . Входящий в формулу (75) безразмерный частотный параметр X (напомним, что X = д/р ) определяется из решения уравнения (54). Значения частот, определенных для различных значений a и h , приведены в табл. 1. Далее получим значения основной частоты колебаний рассматриваемой трехслойной пластины с помощью метода конечных элементов. Для этих целей воспользуемся пакетом COSMOS/M [5]. Моделирование трехслойной пластины было выполнено с помощью конечного элемента SHELL4L, который позволяет рассчитывать трехслойные конструкции. Частоты колебаний рассматриваемой трехслойной пластины, найденные методом конечных элементов, приведены в табл. 2. Сравнение данных таблиц позволяет сделать вывод, что разница между частотами, вычисленными разными способами, не превышает 5 %.

Та ким образом, решена задача определения основной частоты колебаний трехслойной пластины, три края которой жестко закреплены, а один свободен. Для решения уравнений движения был использован метод Канторовича и обобщенный метод Галеркина. Была выполнена верификация разработанной модели вычисления основной частоты колебаний. Определение основной частоты колебаний трехслойной пла стины может быть надежно, без значительных вычислительных усилий выполнено по формулам, предложенным в статье. Полученные формулы окажутся особенно полез-

Частоты колебаний, вычисленные

Таблица 1

с учетом инерции поворота

h , м	a , м
	1	3	5
0,01	102,23	21,771	17,017
0,05	304,381	66,563	52,124
0,10	440,017	99,286	77,931

Таблица 2

Частоты колебаний, вычисленные методом конечных элементов

h , м	a , м
	1	3	5
0,01	99,759	21,614	16,911
0,05	293,335	65,816	51,694
0,10	420,151	97,888	77,167

ными при проектировании трехслойных пластин, когда ограничения накладываются на основную частоту колебаний.