Определение основной частоты колебаний трехслойной панели корпуса космического аппарата
Автор: Деев П.О., Синьковский Ф.К.
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Математика, механика, информатика
Статья в выпуске: 1 т.18, 2017 года.
Бесплатный доступ
Трехслойные панели широко применяются в составе корпусов современных космических аппаратов и обладают различными способами закрепления краев. При проектировании таких панелей всегда существует потребность в аналитической формуле, позволяющей с приемлемой точностью определять основную частоту колебаний, которая является удобной оценкой эффективности трехслойной конструкции, учитывающей взаимное влияние ее жесткости и массы. Решена задача определения первой частоты колебаний трехслойной пластины с жестко закрепленными краями. Для решения уравнений движения был использован метод Галеркина. В качестве функций, аппроксимирующих форму пластины при колебаниях, принято решение задачи об изгибе балки с жестко заделанными краями под действием равномерно распределенной нагрузки. В результате, задача сведена к определению безразмерного частотного параметра, зависящего от геометрических, упругих и инерциальных характеристик трехслойной панели. Частотный параметр вычислен как с учетом, так и без учета инерции поворота нормали. В последнем случае для частотного параметра и частоты получены аналитические формулы. На конкретных примерах выполнен анализ влияния размеров трехслойной пластины, упругих характеристик и плотности материалов на частоту колебаний основного тона. Расчеты проводились с использованием полученных формул и в конечно-элементном пакете. Сравнение результатов показало, что первая частота колебаний закрепленной по контуру трехслойной пластины может быть с достаточной точностью рассчитана по полученной аналитической формуле, что особенно полезно при проектировании трехслойных панелей, когда ограничения накладываются на первую частоту колебаний.
Трехслойная панель, корпус космического аппарата, основная частота колебаний, метод галеркина, аналитическая формула, проектирование
Короткий адрес: https://sciup.org/148177688
IDR: 148177688 | УДК: 67.05
Текст научной статьи Определение основной частоты колебаний трехслойной панели корпуса космического аппарата
Введение. Трехслойные панели широко применяются в составе корпусов современных космических аппаратов и обладают различными способами закрепления краев (рис. 1).

Рис. 1. Трехслойные несущие панели
Динамический анализ является важной частью расчетов трехслойных панелей. Задачи определения частот и форм колебаний трехслойных пластин привлекали внимание многих исследователей. Впервые уравнения движения трехслойной пластины были получены и решены в статьях [1–4]. В последовавших затем исследованиях были предложены разнообразные динамические модели трехслойных пластин, на основе которых были решены многочисленные задачи колебаний этих конструкций. Разработанные модели и методы определения частот и форм колебаний трехслойных пластин нашли свое отражение в обзорах [5–9]. Результаты динамических расчетов трехслойных пластин представлены в работах [10–16].
Трехслойные пластины как несущие конструкции обладают граничными условиями, соответствующими жесткой заделке. Для такой пластины получить решение динамической задачи весьма сложно. Поэтому большинство исследований, посвященных колебаниям трехслойных пластин, выполнено для граничных условий, соответствующих шарнирному закреплению сторон.
Среди задач динамики трехслойных пластин особое место занимает задача определения основной частоты колебаний. Дело в том, что величина частоты зависит от отношения изгибной жесткости пластины к массе единицы поверхности. При этом увеличение изгибной жесткости пластины всегда сопровождается увеличением массы единицы поверхности. Поэтому основная частота колебаний является удобной оценкой эффективности трехслойной пластины, учитывающей взаимное влияние жесткости и массы конструкции. Высокая эффективность трехслойных пластин обусловлена именно тем, что их структура, как никакая иная, позволяет обеспечить значительное увеличение изгибной жесткости при небольшом увеличении массы единицы поверхности. При реальном проектировании защемленных по контуру пластин всегда существует потребность в аналитической формуле, позволяющей с приемлемой точностью определять основную частоту колебаний.
Постановка задачи. Для описания движения пластины в статье использованы уравнения сдвиговой теории пластин, основы которой были заложены в работах [17] и [18] и которая получила широкое распространение при анализе слоистых пластин. Рассмотрим трехслойную пластину, состоящую из одинаковых композитных несущих слоев и ортотропного заполнителя. Срединную плоскость пластины отнесем к системе координат x , y , z . Обозначим через a и b размеры пластины в плане, а через t и δ – суммарную толщину несущих слоев и заполнителя (рис. 2).
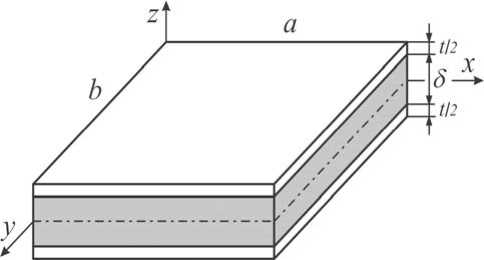
Рис. 2. Трехслойная пластина
Для описания колебаний трехслойной пластины воспользуемся системой уравнений, которая включает уравнения движения:
x + y -B = 0
∂x+ ∂yBρ ∂τ2 0,
∂Mx + ∂Mхy ∂x∂yх
∂M∂M
xy + y -Qy
∂x∂y
--
-
D ρ ∂2θ х = 0, ∂τ ∂ 2 θ
D ρ 2 y = 0,
∂τ
физические соотношения:
M x = D 11 χ x + D 12 χ y , M y = D 21 χ x + D 22 χ y ,
Mxy = D 33 χ xy , Qx = Kx ψ x , Qy = Ky ψ y ,
геометрические соотношения:
X x
д0
, X у д x
50 у д0х д0 у
--<-, x = —— +——, д у y д у д x
а д w
V x =0 X + ~ , V у =0 у д x
д w
+--.
д у
Система уравнений имеет в совокупности шестой порядок по переменным x , у , поэтому на каждом из закрепленных краев пластины надо поставить по три граничных условия, т. е.
В уравнениях (1)-(3) т - время; Q x , Q y - перерезывающие силы; M x , М у - изгибающие моменты; х, X v — кривизны срединной плоскости; x x), - кручение срединной плоскости; у x , у у - осредненные по толщине деформации поперечного сдвига; w - прогиб пластины; 6 x , 6 у - углы поворота нормали к срединной плоскости; D 11 , D 12, D 21, D 22 , D 33 - изгибные жесткости пластины ( D 12 = D 21); B р - инерциальный параметр; D р - параметр, обусловленный инерцией поворота нормали к срединной плоскости.
Получим уравнение движения, содержащие в качестве неизвестных прогиб w и углы поворота 6 x , 6 у . Последовательно подставляя (2) и (3) в (1), получим
при x = 0, a w = 0, 0Y = 0, 0. = 0, x у (7)
при у = 0, b w = 0, 0 x = 0, 0 у = 0.
Определим жесткостные и инерциальные параметры трехслойной пластины. Будем в дальнейшем полагать, что несущие слои являются однородными и ортотропными. Тогда будем иметь t3
D mn = A mnt 12 ^ mn ( mn = 11, 12, 22, 33),
K x = G xz 53Z xz , К у = G yz 55Z yz , (8)
B p = P t t Z p ,
D Р
- t 3 .
= Р/ — S P .
t 12
д2 w д2 w д0х д0у кх —г+к, —Г+К -+К .
x д x 2 у д у 2 x д x у д у
в Ру = °- дт
Здесь
„ д w п д20 п д20х
- К —+ D i— xL + d33— xL x д x 11 д x 2 33 д у 2
^ mn =^ +
Amin S 5
Amnt t
^=^4, Р t t 3
, д20„ д20_.
—К 0 + (Dj2 + D33)--Dр—у = 0, x x v 12 337 дxду дт2
„ _, S S 2
S =1 + 3 — + 3—, Z t t2
— К, ' + ( D ,+ D33 ;"
у д у ( 21 33 ) д x д у
д 20 у
+ D 22-- у +
22 д у 2
SfS + G xz s t I t G xzt
д20 д 20у
+ D 33— ^ — К у 0 у — D Р = °.
д x дт
Z yz
Рассматривая свободные колебания пластины, представим решение уравнений (4) в виде
sfs + G yz S ' t t t Gyzt у
Z p = 1 +^7
P t t
w ( x , у , т ) = w ( x , у ) e i ют , 0 x ( x , у , т ) = 0 x ( x , у ) e i ют 0 у ( x , у , т ) = 0 у ( x , у ) e — i ют ,
где ю - круговая частота колебаний; i = V—1. Функции w ( x , у ), 6 x ( x , у ), 6 у ( x , у ) определяют форму пластины при колебаниях.
Подставляя (5) в (4), получим следующую систему однородных дифференциальных уравнений:
, д2 w д2 w д0 x д0 у 2
х —т + К, —у + К --+ К --+ B to w = 0, x д x 2 у д у 2 x д x у д у Р
д w п д20х п д20х
— Кх — + D u— у + D 33— у x д x 11 9х2 33 ду2
. / Xд20 Л
—К 0Х+ (D12 + D33)---у + Do to20 = 0, x x v 12 33 7 дxду Р x
д w п \ д20 x д 2 0 у
—К+ D-) + D-vk+ D?? + у ду ( 21 33 )дxду 22 ду2
д20„ 2
+ D 33 ^ X 2 У■ — К у 0 у + D p to20 у = 0, здесь и далее w = w ( x , у ), 6 x = 6 x ( x , у ), 6 у = 6 у ( x , у ).
В уравнениях (8), (9) A mnt , A mn 5 ( mn = 11, 12, 22, 33) -коэффициенты жесткости несущего слоя и заполнителя; G xzt , G yzt , G xz 5 , G yz § - трансверсальные модули сдвига несущего слоя и заполнителя; р t , р5 - плотности материалов несущего слоя и заполнителя. Для ортотропного материала A 11 s = E xs , A 22 s = E ys , A 12 s =
E xs vxys , A 33 s Gxys , где s t ,5; E xs Exs /(1 - V xys V yxs ),
E ys = Е уХ /(1 - V xyS V yxS ); E xs , E ys - модули упругости в направлениях x и у соответственно; v xys , v yxs - коэффициенты Пуассона; G xys - модуль сдвига в плоскости xy. Если материал несущих слоев или заполнителя изотропен, то тогда A 11 s = A 22s = Es , A 12 s = Esvs , A 33 s =
Gs 0,5(1 V s ) Es , Gxzs Gyzs Gs , где s t ,5; Es = E s /(1 - vs 2 ); E s - модуль упругости; G s - модуль сдвига; V s - коэффициент Пуассона.
Выбор функций, аппроксимирующих прогиб и углы поворота. Для решения однородной краевой задачи (6), (7) необходимо выбрать функции, которые аппроксимируют форму пластины, соответствующую основному тону колебаний. В качестве таких функций можно принять решение задачи об изгибе балки с жестко закрепленными концами под действием равномерно распределенной нагрузки (рис. 3).
Напряженно-деформированное состояние балки в рамках модели, учитывающей деформации поперечного сдвига, описывается следующими уравнениями:
dQdM
Л + p = 0, —д--Q = 0, M = DX, dxdx d 9
Q = K V , X = , V = 9 + .
dxdx
где p – действующая нагрузка; M , Q – изгибающий момент и перерезывающая сила; χ – кривизна продольной оси балки; ψ – деформация сдвига; w – прогиб балки; θ – угол поворота поперечного сечения; D , K – изгибная и сдвиговая жесткости.
Безразмерный параметр γ характеризует сдвиговую податливость балки. Функции V и U определяют форму балки, которая находится под действием равномерно распределенной нагрузки. Из полученного решения (14), (15) и уравнений (10) следует, что при x = 0, 1 9 = 0, v = -dw / dx = ± pl / (2 K ). Тогда равнодействующая нагрузки pl уравновешивается краевыми усилиями Q = K v = ± p1 1 2.
Решение уравнений движения. Учитывая равенства (15), представим решение уравнений (6) в следующем виде:
w = FU x U y , 9 x = T x V x U y , 9 y = T y U x V y . (17)
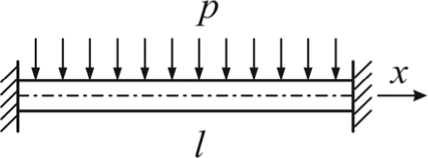
Рис. 3. Балка под действием равномерной нагрузки
Здесь F , T x , T y – неизвестные числа; U x , U y , V x , V y – базисные функции, определяемые выражениями
U x
U y
x I x 1 I
— I--1
a | a J
y Iy - 1) b I b J
x I x 1)
-I—ll-Пу x a | a J
у I y b I b
-1|- 12yу
Из решения уравнений (10) для угла поворота θ и прогиба w можно получить следующие выражения:
I т2 I xx x
Vx 2 7 3 +1 , a2a
Vy =
I J-”2 'I y 2 - 3 y +1 , b I b2 b J
где
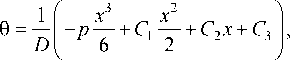
Y x
D 11
Kxa 2
Y
y
D 22
K y b 2 .
22 2
x I x 1 I I 1 x w = p - + Cx--
2 I 12 D K I 1 I K 6 D
^^^^^^B
- C2-— C 3- + C 4, 2 2 D 3 D 4
Безразмерные параметры γ x и γ y характеризуют сдвиговые податливости пластины. Выбранные функции (17) удовлетворяют граничным условиям (7).
Подставляя равенства (17) в дифференциальные уравнения (6), получим следующие невязки:
где C 1 , C 2 , C 3 , C 4 – произвольные постоянные. Для их определения воспользуемся граничными условиями на концах балки
I Kd ' U x x dx x
d2Uy " dy 2
9 = 0, w = 0 при x = 0, 1 , (12)
где l – длина балки (рис. 3).
Подставляя (11) в (12), найдем
C 1 = p 2, C 2 =- p -, C 3 = 0, C 4 = 0. (13)
dV dV
+ K x ; V x U y T x + K y U x + B P ^^U x U y F ,
R x ( x , y , F , T x , T y ) = - K x dU^UyF + dx
Принимая во внимание равенства (13), представим выражения (11) в следующем виде:
'n d 2 V + Dn^x dx
d U I
—^ V x - K x V x U y
dy2 J
T +
x
Здесь
где
9 = —^—V , w = pl— U .
12 Dl 24 D
V = x 2 x- - 3 x + 1 ;
11 12 1 J
U = x I x-1
11 1
x I x
- 1 I- 12 y
D
Y " ki 2.
+ ( D 12 + D 33 ) dU x dV ^ T y + D p ® 2 V x U y T x , (20)
dx dy
Ry (x, y, F, Tx, Ty ) = - KyUx—LF + dy
+ ( D2 i+ D 3 з) dV x dU ^ T +
21 33 dx dy x
L d 2 V „ d 2 U, L „ 7 „
+ D22^U + D 33-- 5 VVv - KUV T + D to UFT .
22 dy2 x 33 dx2 y y x y y p x y x
Следуя методу Галеркина, потребуем, чтобы невязки R , R x , R y были ортогональны к соответствующим базисным функциям, т. е.
jjR (x, y, F, Tx, Ty UxUydxdy = 0, j jRx (x,y,F,Tx,Ty )yxUydxdy = 0, (21)
j j R y ( x , y , F , T x , T y U . Vdxdv = 0.
Подставляя (20) в (21), будем иметь
( K x I 2 x I 1 y + K y I 1 x I 2 y ) F + K x I 3 x I 1 y T x +
+ K x I 1 x I 3 yTy + B p ®11 1 x I 1 y F = 0,
a 33 = 3
- — Y 1 x + 12 ₽ 2 Y 2 x a Y y
Y a 12 = a 21 = 6a--- Y 1 y ,
Y
, 1 Y3 y a13 = a 31 = 6--Y1 x a Y y
,
a 23 = a 32 = 36 ( P 1 +в 2 ) y 3 x Y 3 y ,
b11 = Y 1 x Y 1 y , b 22 = 3 r x Y 1 y , b 33 = 3 r y Y 1 x ,
\D 1^ b 2 , p 1 = Г " 1^ , p 2 = Y D 31- , D 22 a D 11 D 22 D 11 D 22
- K x J 3 x I 1 y F + ( D 11 J 2 x I 1 y + D 33 J 1 x I 2 y - K x J 1 x I 1 y ) x X T x + ( D 12 + D 33 ) J 3 x I 3 y T y + D p ® J 1 x I 1 y T x = 0,
Dp rx = TV, ry Bp a
D p
B p b 2 ,
— K y I 1 xI 3 y F + ( D 22 1 1 xJ 2 y + D 33 I 2 x I 1 y — K y I 1 xJ 1 y ) T y +
B p ®2 a 2 b 2 n = —,
D 11 D 22
+ ( D 21 + D 33 ) 1 3 x J 3 y T x + D p ® 2 1 1 x J 1 y T y = 0.
Подставляя U x , U y , V x , V y из (18) в соотношения (23), после интегрирования найдем
I = a Y 1 x I = b Y 1 y 1 x 630 , 1 y 630 ,
J, = — J, =
1 x 210, 1 y 210,
I = 2 Y 2 x I = 2 Y 2 y 2 x 105 a , 2 y 105 b ,
J 2 x =
r, J 2 y =- (23) 5 a 5 b
I = Y 3 x I = Y 3 y 3 x 105, 3 y 105,
J 3 x
= Y 3 x J = Y 3 y
105, 3 y 105,
Величина η, входящая в уравнения (25) и определяемая равенством (30), является безразмерным частотным параметром. Таким образом, задача об определении основной частоты колебаний защемленной по контуру трехслойной пластины сведена к вычислению параметра η, при котором однородная система (25) будет иметь решение, отличное от нуля.
Определение частотного параметра η и частоты колебаний ω. Представим систему (25) в виде следующего матричного уравнения:
( A - n B ) F = 0 , (31)
где
где
-
Y 1 x = 1 + 108 Y x + 3024 y 2 , Y 2 x = 1 + 84 y x + 2520 y 2 ,
-
Y 3 x = 1 + 42 Y x , Y 1 y = 1 + 108 Y y + 3024 y 2 , (24)
Y 2 y = 1 + 84 Y y + 2520 Y 2 , Y 3 y = 1 + 42 y y .
Подставим значения интегралов (23) в уравнения (22) и затем получившиеся соотношения приведем к безразмерному виду, умножив каждое из них на величину ab D11D22 . В результате преобразований получим a11 F + a12Fx + a13Fy - nb11 F = 0, a21F + a22Fx + a23Fy - Пb22Fx = 0, (25)
F = ^
F 1 [ a Fx L A = L
x
. F y J I a
a 12
a 22
a 32
a13 | b 11 a 23 [ , B =1 0 a 33 J [ 0
0 0 1
b 22 0 ^ . (32)
0 b 33
Здесь
a 31 F + a 32 Fx + a 33 F y - П b 33 F y = 0.
F x = aT x , F y = bT y ,
a 11 = 12 a-^ y I Y x
1 Y 2
■ +---:
1 y a y ,
Y 1 x ,
I Y3t a22 = 3I a---Y1 y +12₽2Y2
Y
,
Традиционный подход к определению собственных значений η предполагает решение характеристического уравнения det ( A – η B ) = 0, которое в раскрытом виде представляет собой полином третьей степени. В уравнении (31) матрица A симметричная, а диагональная матрица B очевидно симметричная и положительно определенная. Поэтому все собственные значения обобщенной задачи являются вещественными и, как показывает практика вычислений, положительными. Минимальное из трех собственных значений будет определять требуемый частотный параметр η. Величина η зависит от параметров γ x , γ y , α, β 1 , β 2 , r x , r y , которые содержат всю информацию о жесткостных, геометрических и инерциальных характеристиках трехслойной пластины.
Определение частотного параметра требует некоторых вычислительных усилий, которых можно избежать, если учесть, что инерция поворота мало влияет на частоту колебаний основного тона. Получим формулу для η, в которой не будет инерционных составляющих, связанных с поворотом нормали к срединной плоскости трехслойной пластины. Примем D ρ = 0. Тогда r x = r y = 0, и, как следствие, b 22 = b 33 = 0.
Запишем второе и третье уравнения системы (25),
учитывая, что a23 = a32, в следующем виде a 22 Fx + a 23 Fy = -a12 F, a 23 Fx + a 33 Fy = - a13 F. (33)
Из (33) найдем
a = . , P 1 = A , , ₽ 2 = ,.A 33‘ . (42)
A 22 t a A 11 t A 22 t A 11 t A 22 t
Подставляя в формулу (37) ξ 11 = ξ 22 = ξ, будем иметь
a 23 a i3 a i2 a 33
F x = ----------- 2-- F :
a 22 a 33 - a 23
F y =
a 23 a 12 a 13 a 22 77
a 22 a 33 - a 23
Подставляя (34) в первое уравнение системы (25), получим для η следующее выражение:
1 Л 1 /у A 11 t A 22 Z to = — X---,--.
2 ab y 3p t Z p
n =
a 11 a 22 a 33
+ 2 a i2 a i3 a 23
1 - « 11 a 223 - a 22 a 23 - a 33 0 2 b ll a 22 a 33 - a 23
Получим выражение для частоты колебаний трехслойной пластины. Безразмерный частотный параметр η может быть определен из решения обобщенной задачи (31) или из формулы (37). При известном η из формулы (30) найдем частоту колебаний, т. е.
Определим частотный параметр η и частоту колебаний основного тона f для квадратной трехслойной пластины с изотропными несущими слоями и легким заполнителем. Коэффициенты жесткости и модули сдвига материала несущих слоев имеют следующий вид:
A 11 1 = A 22 1 = Et , A 12 1 = vtEt , A 33 1 =
DD
Ю = А V 11 22 , (36)
aby Bp где X = X .
Используя равенства (8), преобразуем формулу (36)
G xzt = G yzt = G t , G xz 5 = G yz 5
Подставляя (44) в (41), получим
1 - v t f
E , 2 t (44)
= G 5
1 E Z 1
Yx =Y y =Y = ----^, 12 G5 Z 5 a t t2
к виду
1t ю = —X—
2 ab
J У A ll t A 22 1 У ^ 11 ^ 22 3 p t Z p
Z = Z xz =Z
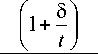
.
51 5 G 5 I
-I +X I
1 ^ 1 Gt j
Выражение (37) определяет частоту колебаний основного тона закрепленной по контуру трехслойной пластины.
Численный анализ и верификация результатов. Прежде чем приступить к численному анализу, получим выражения, определяющие параметры γ x , γ y , α, β 1 , β2, r x , r y , от которых зависит величина η. Подставляя (8) в (19), (28) и (30), будем иметь
Учитывая равенства (45), определим для рассматриваемой пластины сдвиговые параметры γ ix , γ iy ( i = 1, 2, 3, 4). Из уравнений (24) и (39) будем иметь
Y 1 x =Y 1 y =Y 1 = 1 + 108 Y + 3024 Y 2 ,
Y 2 x =Y 2 y =Y 2 = 1 + 84 Y + 2520 y 2 , (46)
Y 3 x = Y 3 y = Y 3 = 1 + 42 y , Y 4 x = Y 4 y = Y 4 = 1 + 60 y .
Y.
1 A 11t £ 11 1
12 G xz 5 Z xz 5 a ’ t t 2
Y y
1 A 22 t ^ 22 1
12 G yz 5 Z yz 5 b ’ t t 2
I A 11t ^ 11 b p = A 12 t ^ 12
A 22 1 Z 22 a У A 11 t A 22 t ^ 11 ^ 22
Подстановка (44) в (42) при a = b дает a = 1, ₽1 = vt, ₽2 = -^"L. (47)
Для квадратной пластины инерционные парамет-
A 33 1 Z 33
11 t A 22 1 Z 11 Z 22
ры r x и r y (40) равны, т. е.
1 Zp X r = 1 Zp X
12 Z p a" ’ y 12 Z p b .
1 Z p 1
r x = r y = r = T5 --Г.
12 Zp a t2
Если материал заполнителя легкий, т. е. обладает малой жесткостью в направлениях x и y , то можно принять A mn δ = 0 ( mn = 11, 12, 22, 33). Тогда из уравнения (9) следует, что ξ mn = ξ ( mn = 11, 12, 22, 33), и равенства (38), (39) примут следующий вид:
Определим коэффициенты матрицы А и В однородной системы линейных алгебраических уравнений (31). Учитывая равенства (46), (47) и (48), из соотношений (27) будем иметь a- = 2411I2-, a 22 = a 33 = 3 ^1^3 + 6 (1- vt )Y2 ,
Y L Y J
= 1 Ant Z 1 Y = 1 A 22 1 Z 1
12 G x Z 5 Z xz 5 a , Y y 12 G yz 5 Z yz 5 b ,
a 12 = a 13 = a 21 = a 31 = 6 — , (49)
Y a 23 = a 32 = 18 (1 + vt )y3, b11 =Y1, b22 = b33 = 3 r Y1.
При известных коэффициентах (49) частотный параметр η определяется как минимальное собственное значение однородной системы (31).
Формула для частоты колебаний квадратной трехслойной пластины с изотропными несущими слоями и легким заполнителем может быть получена из (43), если принять a = b и A 11 t =A 22 t =E t . Тогда
Et ^
N 3 p t Z p
1t и V'-
2a2
Для того, чтобы динамический анализ был более конкретным, зададим характеристики материалов и размеры. Пусть несущие слои выполнены из алюминиевого сплава с E t = 70 ГПа, v t = 0,3, G t = 27 ГПа, ρ t = 2700 кг/м3. Рассмотрим два типа заполнителя. Один из них будем называть податливым заполнителем, а другой – жестким заполнителем. Пусть у податливого заполнителя G δ = 80 МПа, ρ δ = 30 кг/м3, а у жесткого заполнителя G δ = 400 МПа, ρ δ = 80 кг/м3. Отметим, что в заполнителях увеличение жесткости, т. е. модуля сдвига G δ , происходит всегда с одновременным увеличением плотности материала ρ δ .
Зададим размеры трехслойной пластины. Пусть суммарная толщина несущих слоев t = 0,001 м, толщина заполнителя δ принимает значения 0,02 и 0,1 м, а размер пластины в плане a принимает значения 0,5, 1,0 и 2,0 м.
Для вычисления круговой частоты колебаний воспользуемся формулой (50). При этом частотный параметр η будет определен в зависимости от того, учитывается или не учитывается влияние инерции поворота на динамическое поведение трехслойной пластины.
В табл. 1 приведены частоты колебаний f = ω/2π в герцах для трехслойных пластин с податливым и жестким заполнителями.
Таблица 1
Частота колебаний f (Гц) трехслойной пластины с податливым и жестким заполнителем
|
δ |
Податливый |
Жесткий |
||||
|
a |
||||||
|
0,5 |
1,0 |
2,0 |
0,5 |
1,0 |
2,0 |
|
|
0,02 |
759,2 760,4 |
247,4 247,5 |
68,1 68,2 |
886,1 888,3 |
240,7 240,9 |
61,6 61,6 |
|
0,10 |
1571,3 1574,1 |
656 658,1 |
222,5 223,1 |
2023,5 2048,8 |
664,8 670,6 |
185,0 185,5 |
В каждой из ячеек табл. 1 первое значение частоты определено с учетом инерции поворота ( D ρ ≠ 0), а второе – без учета инерции поворота ( D ρ = 0). Частотный параметр η для первого значения f находится как минимальное собственное число однородной системы (31). Частотный параметр η для второго в ячейке значения f был определен с помощью формулы (50).
Анализ данных из табл. 1 позволяет сделать выводы о влиянии размеров трехслойной пластины, упругих характеристик и плотности составляющих материалов на частоту колебаний основного тона. Отметим, что влияние инерционной составляющей Dρ на основную частоту колебаний невелико, даже для толстых пла- стин (a = 0,5 м, δ = 0,1 м). Из табл. 1 видно, что разница между частотами, вычисленными с учетом и без учета инерции поворота, не превышает 0,3 %.
Сравнивая данные в соответствующих ячейках двух таблиц, можно заметить, что увеличение жесткости заполнителя приводит к росту частоты колебаний только для пластин с a = 0,5 м. У пластин с a = 1,0 м, a = 2,0 м увеличение жесткости заполнителя (т. е. увеличение G δ и ρδ) вызывает уменьшение частоты колебаний. Как показывает численный анализ, для пластин с большим отношением a /(δ + t ) такой эффект обусловлен преобладающим влиянием на частоту колебаний плотности заполнителя ρ δ по сравнению с влиянием, которое оказывают на частоту колебаний модуль сдвига G δ . Обнаруженную зависимость f от G δ и ρ δ необходимо учитывать при выборе заполнителя в задачах проектирования трехслойных пластин, когда ограничения накладываются на основную частоту колебаний.
Для проверки полученных результатов определим первую частоту колебаний рассматриваемой трехслойной пластины в пакете ANSYS. Воспользуемся при моделировании пластины конечным элементом SHELL181 с опцией, соответствующей расчету трехслойных конструкций. Форма колебаний пластины показана на рис. 4.
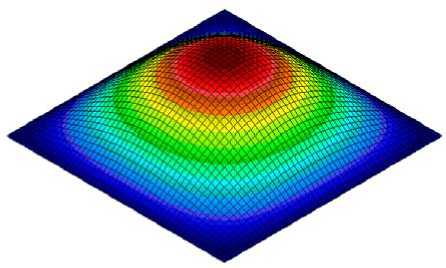
Рис. 4. Форма колебаний квадратной трехслойной пластины, жестко закрепленной по контуру (МКЭ-расчет)
В табл. 2 приведены частоты колебаний трехслойной пластины с податливым и жестким заполнителями, полученные с помощью метода конечных элементов.
Таблица 2
Частоты колебаний f (Гц) трехслойной пластины с податливым и жестким заполнителем (МКЭ)
|
δ |
Податливый |
Жесткий |
||||
|
a |
||||||
|
0,5 |
1,0 |
2,0 |
0,5 |
1,0 |
2,0 |
|
|
0,02 |
754,4 |
245,5 |
67,9 |
881,8 |
240,2 |
61,6 |
|
0,10 |
1561,9 |
652,1 |
221,2 |
2010,7 |
661,4 |
184,5 |
Сравнение результатов, приведенных в табл. 1 и 2, позволяет сделать вывод о том, что частоты, вычисленные методом конечных элементов, мало отличаются от частот, найденных на основе двух моделей, рассматриваемых в настоящей работе. Максимальная разница между данными в табл. 1 и 2 не превышает 1,9 % .
Отметим, что конечно-элементный анализ подтвердил также обнаруженные ранее особенности влияния модуля сдвига заполнителя G δ и его плотности ρ δ на величину частоты колебаний трехслойной пластины.
Выполненный выше анализ результатов дает основание утверждать, что определение первой частоты колебаний закрепленной по контуру квадратной трехслойной пластины вполне может быть выполнено с помощью формул (36) и (37).
Проектирование. Расчеты по определению основной частоты колебаний трехслойной пластины с защемленными краями с использованием соотношений (36) и (37) не требуют значительных вычислительных затрат. Поэтому полученные формулы могут быть особенно полезны на этапе проектирования трехслойных пластин. Продемонстрируем это на примере задачи по выбору толщин заполнителя δ и несущих слоев t для квадратной трехслойной пластины с заданной частотой колебаний f . Пусть несущие слои и заполнитель имеют следующие параметры: E t = 70 ГПа, v t = 0,3, G t = 27 ГПа, ρ t = 2700 кг/м3, G δ = 400 МПа, ρ δ = 80 кг/м3. Размер a = 1,0 м. Определим пространство проектирования в виде неравенств
0,0005 м ≤ t ≤ 0,002 м, 0,02 м ≤δ≤ 0,10 м. (51)
Представим зависимость f (δ, t ) набором двумерных контурных линий (рис. 5). Пусть заданная частота f = 500 Гц. На рис. 5 контурная линия, соответствующая этой частоте, имеет увеличенную толщину.
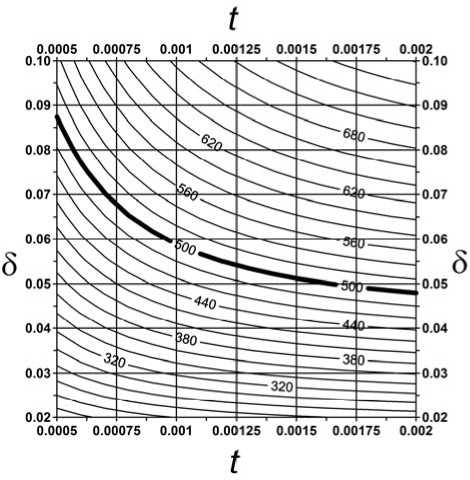
Рис. 5. Зависимость f ( t , δ) в виде набора контурных линий
Очевидно, что заданная частота f может быть реализована при различных сочетаниях t и δ из пространства проектирования (51). Для каждой пары значений t и δ должно выполняться условие
2 π f -ω ( t , δ ) = 0,
где ω – круговая частота колебаний, вычисляемая по формуле (50).
Подставляя (50) в (52), будем иметь
2 π f - 1 λ t
2 a 2
Et ξ 3 ρ t ζ ρ
где λ =η . Для вычисления частотного параметра используются уравнения (30), (35). Задаваясь различными значениями t , решим нелинейное уравнение (53) относительно δ. Для получившейся пары t и δ определим массу пластины, т. е.
m = a 2 ( ρ t t + ρδδ ) . (54)
Результаты вычислений по описанному алгоритму для рассматриваемой пластины приведены на рис. 6 и 7.
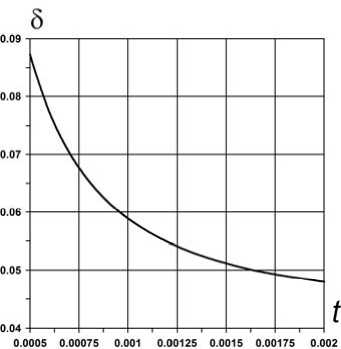
Рис. 6. Зависимость δ( t )
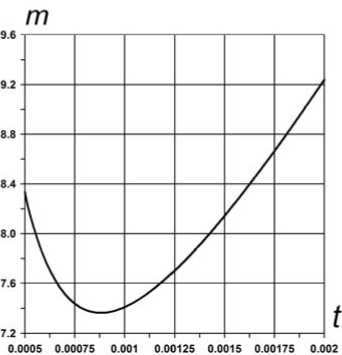
Рис. 7. Зависимость m ( t )
Из анализа полученных данных следует, что с увеличением толщины несущих слоев t толщина заполнителя δ уменьшается (рис. 6). Масса пластины m в рассматриваемом диапазоне измерения t имеет минимум (рис. 7). Таким образом, m min = 7,3657кг, t opt = 0,0009 м, δ opt = 0,0617 м.
Рассмотренный выше подход к определению первой частоты колебаний трехслойной пластины с защемленными краями реализован в вычислительных программах.
Заключение. Решена задача определения первой частоты колебаний трехслойной пластины с жестко закрепленными краями. Для решения уравнений движения был использован метод Галеркина. В качестве функций, аппроксимирующих форму пластины при колебаниях, было принято решение задачи об изгибе балки с жестко заделанными краями под действием равномерно распределенной нагрузки. Эти функции учитывают сдвиговую податливость пластины и удовлетворяют граничным условиям, предполагающим, что на каждом из краев пластины отсутствуют прогиб и два угла поворота нормали к срединной плоскости.
Задача вычисления первой частоты колебаний трехслойной пластины сведена к определению безразмерного частотного параметра, величина которого зависит от геометрических, упругих и инерциальных характеристик трехслойной пластины.
Рассмотрены два подхода к определению частотного параметра, которые отличаются друг от друга в зависимости от того, учитывается или не учитывается влияние инерции поворота на динамическое поведение трехслойной пластины. В первом подходе частотный параметр находился как минимальное собственное число соответствующей системы однородных алгебраических уравнений. При втором подходе для определения частотного параметра была получена аналитическая формула.
На конкретных примерах был выполнен анализ влияния размеров трехслойной пластины, упругих характеристик и плотности соответствующих материалов на частоту колебаний основного тона. Расчеты проводились как с использованием рассматриваемых в работе подходов, так и с помощью метода конечных элементов.
Анализ результатов позволил сделать вывод о том, что определение первой частоты колебаний закрепленных по контуру трехслойных пластин, обладающих разнообразными жесткостными параметрами и размерами, может быть с достаточно высокой точностью выполнено по полученным аналитическим формулам. Эти формулы будут особенно полезны при проектировании трехслойных пластин, когда ограничения накладываются на первую частоту колебаний.
Список литературы Определение основной частоты колебаний трехслойной панели корпуса космического аппарата
- Yu Y. Y. A new theory of elastic sandwich plates -one dimensional core//Journal of Applied Mechanics. 1959. Vol. 26. P. 415-421.
- Yu Y. Y. Simple thickness-shear modes of vibration of infinite sandwich plates//Journal of Applied Mechanics. 1959. Vol. 26. P. 679-681.
- Yu Y. Y. Flexural vibrations of elastic sandwich plates//Journal of Aerospace Sciences. 1960. Vol. 27. P. 272-282.
- Yu Y. Y. Simplified vibration analysis of elastic sandwich plates//Journal of Aerospace Sciences. 1960. Vol. 27. P. 894-900.
- Habip L. M. A survey of modern developments in the analysis of sandwich structures//Applied Mechanics Reviews. 1965. Vol. 18. P. 93-98.
- Ha K. H. Finite-element analysis of sandwich plates: an overview//Computers and Structures. 1990. Vol. 37 (4). P. 397-403.
- Noor A. K., Burton W. S., Bert C. W. Computational models for sandwich plates and shells//Trans. ASME. Applied Mechanics Reviews. 1996. Vol. 49 (3). P. 155-199.
- Librescu L., Hause T. Survey of recent developments in the modeling and behavior of advanced sandwich constructions//Journal of Composite Structures. 2000. Vol. 48 (1-3). P. 1-17.
- Vinson J. R. Sandwich structures//Applied Mechanics Review. 2001. Vol. 54 (3). P. 201-214.
- Zenkert D. An introduction to sandwich construction. London: Chameleon Press, 1995. 277 p.
- Yu Y. Y. Vibrations of elastic plates: linear and nonlinear dynamic, modeling of sandwiches, laminated composites and piezoelectric layers. New York: Springer-Verlag, 1996. 225 p.
- Vinson J. R. The behavior of sandwich structures of isotropic and composite materials. Lancaster: Technomic, 1999. 378 p.
- Kollar L. P., Springer G. S. Mechanics of composite structures. Cambridge: University Press, 2003. 470 p.
- Паймушин В. Н. Точные аналитические решения задачи о плоских формах свободных колебаний прямоугольной пластины со свободными краями//Известия высших учебных заведений. Математика. 2006. № 8. С. 54-62.
- Мущанов В. Ф., Демидов А. И. Расчет трехслойной пластинки, лежащей на винклеровском основании, вариационно-разностным методом//Современное промышленное и гражданское строительство. 2010. Т. 6, № 2. С. 77-91.
- Коган Е. А., Юрченко А. А. Нелинейные колебания защемленных по контуру трехслойных пластин//Проблемы машиностроения и надежности машин. 2010. № 5. С. 25-34.
- Reissner E. The effect of transverse shear deformation on the bending of elastic plates//Trans. ASME. Journal of Applied Mechanics. 1945. Vol. 12 (2). P. 69-77.
- Mindlin R. D. Influence of rotary inertia and shear on flexural motions of isotropic elastic plates//Trans. ASME. Journal of Applied Mechanics. 1951. Vol. 18. P. 31-38.


