Определение остаточного ресурса анизогридной конструкции из полимерного композиционного материала

¹ Большой объем экспериментальных данных по традиционным металлическим материалам, применяемым в космической технике, позволяет на основании статических и динамических испытаний [1] прогнозировать работоспособность космического аппарата (КА) на всем жизненном цикле его эксплуатации.

Для новейших конструкций из полимерного композиционного материала с применением высокомодульных и высокопрочных углеродных волокон, формируемых методом намотки [2, 3], нет достаточно представитель-

manufacturing analysis , residual life.

ного объема испытаний до разрушения, чтобы уверенно прогнозировать работоспособность конструкции при многократном и длительном нагружении.

Если время действия полетных перегрузок ограничено временем работы двигателей ракеты-носителя и разгонного блока, то при наземной эксплуатации время нагружения КА при его консольном положении может достигать десятков суток.

Кроме того, необходимость контроля жесткости каждого конического адаптера (рис. 1) предполагает статическое нагружение, что расходует часть ресурса несущей способности.

Havko-

ЖГРАДА

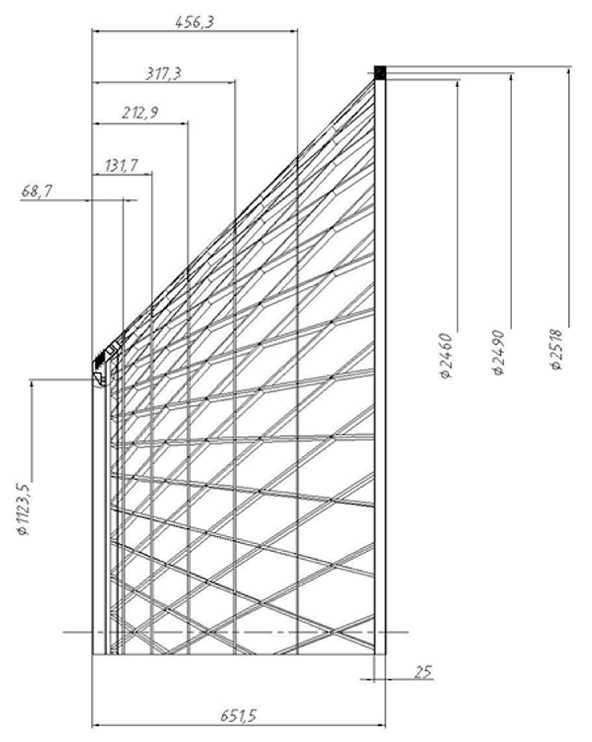
Рис. 1. Габаритные размеры адаптера конического

Кинетическая концепция прочности академика С. Н. Журкова [4, 5] дает ключ к решению проблемы прочности при длительном нагружении с учетом температурных условий, в том числе и при усталостном нагружении.

Главным действующим фактором при разрушении оказывается не внешняя сила, а тепловое движение атомов, порождающее энергетические флуктуации. Именно флуктуации разрывают межатомные связи, что и ведет в итоге к разрушению твердого тела. Внешняя сила обеспечивает направленность разрывного действия флуктуаций, без чего не может развиваться разрушение [4, 5, 6].

Длительная прочность или долговечность определяется следующей зависимостью (формула Журкова):

t = to^exp(U0 - v°yRT (с), (1) где t0 – период колебаний атомов, с; t0 = 10-13, с; U0 - энергия активации, ккал/моль; v -структурно-чувствительный коэффициент, ккал-мм2/молыкг; о - действующее напря жение, кг/мм2; R - газовая постоянная, ккал/ моль∙К; Т – температура, К.

В металлах разрушение всегда проис -ходит посредством зарождения и роста магистральной трещины. В противоположность этому потеря несущей способности волокнистых композитов является следствием развития целого ряда процессов разрушения: растрескивания матрицы, отслоения волокон от матрицы, разрушения волокон и появления трещин между соседними слоями волокон [7].

Поскольку механизмы разрушения композиционных материалов разные, в зависимости от того, какой элемент композита (волокно, матрица или поверхность раздела волокно–матрица) в данном нагруженном сечении элемента конструкции находится в перенапряженном состоянии, по такому сценарию и будет развиваться разрушение.

Наименьшая длительная прочность определяется прочностью адгезионных связей и свойствами матрицы.

В работе [5] приведены силовые зависимости долговечности для стеклопластика (рис. 2).

Силовым зависимостям, приведенным на рис. 2, соответствует энергия активации U 0 = 39 ккал/моль при нагружении в воздушной среде и U ₀ = 31 ккал/моль при нагружении в воде.

Структурно-чувствительный коэффициент при нагружении вдоль волокон ν = 0,77 ккал^мм2/молыкг в воздухе и v = 0,5 ккал^мм2/ моль∙кг в воде. При нагружении под углом 45 градусов структурно-чувствительные коэффициенты соответственно равны: ν = 2,15 ккал^мм2/молыкг и v = 1,68 ккал^мм2/ моль∙кг.

Длительная прочность как на воздухе, так и в воде определяется матрицей. Присутствие ра на 120-й секунде при уровне напряжений 21,3 кг/мм2.

Величина напряжений получена c учетом особенностей распределения усилий в спиральных ребрах при совместном действии осевой, перерезывающей сил и изгибающего момента на коническую конструкцию с углом конусности 45 градусов.

Наиболее нагруженными элементами конструкции является группа спиральных ребер, расположенных в зоне нейтральной оси опорного сечения адаптера и идущих в направлении 3 плоскости стабилизации (по условиям испытаний) и работающих в условиях осевого сжатия и поперечного изгиба.

Для данного напряженно-деформированного состояния в элементе конструкции,

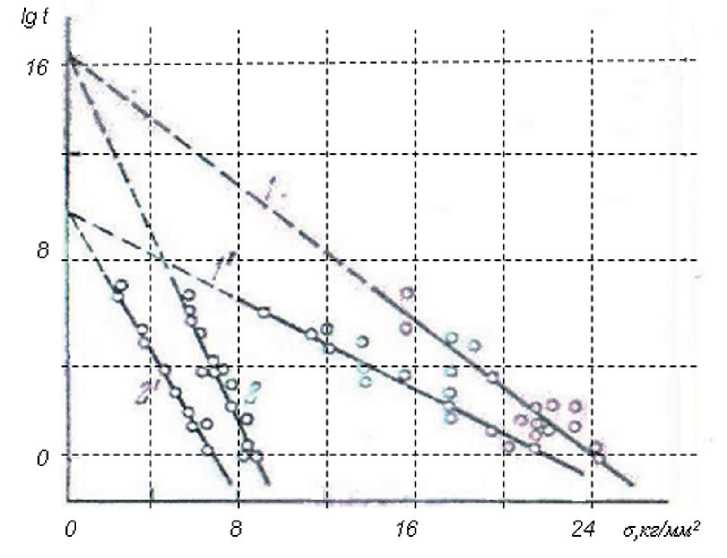
Рис. 2. Силовые зависимости долговечности для стеклопластика: 1, 2 – в воздушной среде; 1', 2' – в воде; 1 и 1' – ось стеклопластика параллельна оси нагружения; 2 и 2' – ось стеклопластика расположена под углом 45º к оси нагружения [5]

воды уменьшает адгезионную прочность.

При испытаниях до разрушения конического адаптера были реализованы разные режимы нагружения.

Суммарная длительность нагружения первого адаптера составляла 20 мин, и разрушение соответствовало уровню напряжений в наиболее нагруженных спиральных ребрах 18,0 кг/мм2.

Режим непрерывного увеличения нагрузки привел к разрушению второго адапте- представляющем собой слоистую структуру при толщине прослоек связующего, равной толщине армированного слоя, развиваются растягивающие матрицу напряжения, которые приводят к нарушению сплошности с последующей потерей устойчивости отдельных волокон и системы в целом. Разрушение носит лавинообразный характер, и обычными средствами наблюдений и измерений нельзя выделить начальную стадию разрушения.

HAVKO____________

Ж ГРАДА

Механизм разрушения элементов конструкции двух разрушенных адаптеров совершенно одинаков.

Логарифмируя зависимость (1), получим зависимость для определения по экспериментальным данным значения энергии активации и структурно-чувствительного коэффициента для данного механизма разрушения адаптера

U (σ) = U ₀– νσ = 2,3 RT (13 + lg t ).     (2)

Подставляя в (2) значения времени дей- ⁶ ствия нагрузок при испытаниях адаптеров lg t ₁ = 3,08 и расчетную величину о 1 = 18,0 кг/мм², затем lg 1 ₂ = 2,08 и о₂ = 21,3 кг/мм² при Т = 293 К и R = 0,002 ккал/моль К, получим для реализованного механизма разрушения значения энергии активации матрицы ЭХД-МД U 0 = 29,5 ккал/моль и структурно-чувствительного коэффициента v = 0,44 ккал мм²/молыкг.

На основе полученной математической модели долговечности может быть рекомендован следующий алгоритм прогнозирования остаточного ресурса после очередного этапа жизненного цикла КА:

• 1.    Определить максимальные напряжения сжатия в элементах конструкции на данном этапе эксплуатации. Выделить критичные элементы.

• 2.    По силовой зависимости долговечности от напряжений (1) определить критическое время t_C до разрушения.

• 3.    По соотношению длительности t . воздействия с данным уровнем напряжений и критического времени t. _C определить использованный ресурс K = t / t _C.

• 4.    По формуле 1 - K = K ₀ . определить остаточный ресурс K _{0 i} после данного этапа жизненного цикла КА.

• 5.    Повторить пп.1–3.

• 6.    Просуммировать с результатом предыдущего этапа эксплуатации, тем самым будет получено значение использованного ресурса перед последующим этапом эксплуатации.

• 7.    Определить остаточный ресурс по п. 4.

• 8.    Повторить пп. 1-7 до завершения миссии КА.

Необходимый ресурс несущей способности определится на основании следующей математической модели:

∑ t_i/t_iC ≤ 1.                     (3)

При определении требуемого ресурса несущей способности и остаточного ресурса кинетическая концепция прочности твердого

№ 1 (1) январь-март 2012

тела позволяет учесть диапазон температур, характерный для данного этапа эксплуатации.

В отличие от металлических конструкций, сетчатые структуры из полимерного композита требуют учета длительности действия нагрузок и температуры при эксплуатации.

Для проверки влияния длительности нагружения были проведены испытания на третьем адаптере в последовательности, приведенной в табл. 1.

В таблице указано время действия приведенной нагрузки, составляющей часть ожидаемой разрушающей нагрузки, пересчитанной к времени длительной прочности, соответствующей 1 с.

В таблице указан остаточный ресурс по мере перехода от одного этапа нагружения к следующему.

Перед последним этапом испытания прогнозируемое время до разрушения при принятых допущениях составляло 270 с. Разрушение произошло после выдержки 300 с.

При анализе использована силовая зависимость долговечности под нагрузкой для углепластика с матрицей из ЭХД-МД, соответствующая энергии активации U (о) = 29,13 ккал/моль (рис. 3) и начальной несущей способности, эквивалентной осевой нагрузке Р _кр= 130 т при времени до разрушения 1 с.

На рис. 3 по оси ординат отложен логарифм времени пребывания под нагрузкой, по оси абсцисс – отношение действующей нагрузки к предельной разрушающей, соответствующей длительности нагружения в течение 1 с. Обозначение этапов нагружения соответствует табл. 1. Состояние разрушения обозначено крестиком.

Таким образом, показана эффективность применения кинетической концепции прочности академика С. Н. Журкова для определения остаточного ресурса несущей способности сетчатой структуры, используемой в качестве адаптера при запуске космического аппарата.

Для уточнения эксплуатационных ограничений целесообразно продолжить исследование сетчатых конструкций в обеспечение требуемой надежности с применением вероятностной модели накопления повреждений [8].

В силу конструктивных и технологических особенностей конический адаптер к началу эксплуатации после проведения приемосдаточных испытаний в соответствии с действующей документацией уже обладает кумулятивными повреждениями, которые мо-

Таблица 1

№ п/п	Величина относительной нагрузки, Р / Р экв кр	Время действия нагрузки, ti , с	Критическое время, tiC , с	Текущий ресурс, ti/tiC	Использованный ресурс, ∑ ti/tiC	Остаточный ресурс, 1 – ∑ ti/tiC
1	0,615	120	2080	0,0597	0,0597	0,9403
2	0,585	120	3640	0,0330	0,0927	0,9073
3	0,214	432 000	5 550 000	0,0778	0,1705	0,8295
4	0,320	432 000	682 000	0,6340	0,8045	0,1955
5	0,470	3600	35 200	0,1020	0,9065	0,0935
6	0,597	300	2 870	0,1045	1,0110	Нет

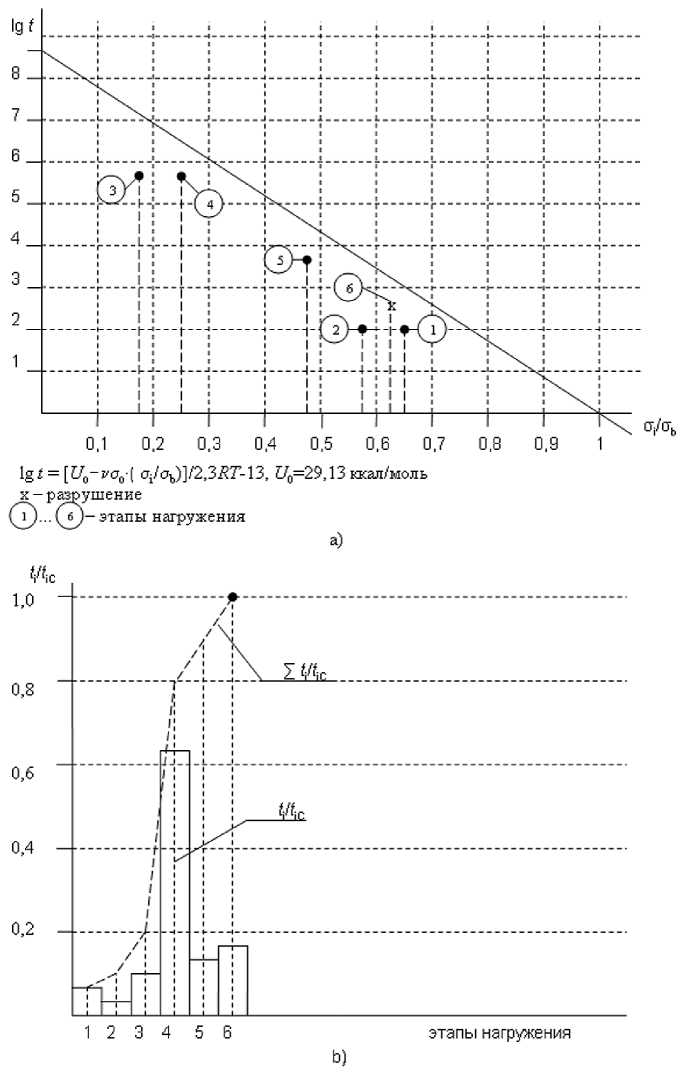
Рис. 3

Havko-

■ ГРАДА

гут быть выявлены только современными неразрушающими методами контроля (типа акустической эмиссии).

Поэтому для оценки влияния механической обработки на несущую способность сетчатой структуры из полимерного материала целесообразно исследование корреляции режимов резания и напряженно деформированного состояния силовых элементов конического адаптера с оценкой степени опасности на основании результатов измерений в процессе обработки.