Определение параметров допустимых дефектов конструкционного стеклопластика на основе теории критических расстояний

ВЕСТНИК ПНИПУ. МЕХАНИКА № 4, 2023PNRPU MECHANICS BULLETIN

В процессе производства изделий из композитных материалов может возникнуть множество дефектов: трещины, сколы, царапины, вмятины, дефекты ударного характера, воздушные макровключения и другие. Такие дефекты могут существенно снизить как статическое, так и усталостное сопротивление конструкций. Существует множество способов повлиять на дефекты (понизить поврежденность материала). Например, автоматизированное управление производственным процессом с помощью искусственного интеллекта, варьирование параметрами производственного процесса и т.д. Помимо оптимизации процесса, постобработка также может влиять на дефекты, описанные выше. Например, локальный ремонт, механическая обработка и т.д. Дефекты могут быть минимизированы путем оптимизации процесса и/или постобработкой, но не могут быть полностью устранены. Поэтому очень важно понимать, как геометрия и расположение дефекта влияют на механические свойства [1–6].

Помимо внутренних дефектов, в конструкциях во время их эксплуатации могут возникать некоторые повреждения, такие как зазубрины и вмятины. Кроме того, отверстия, канавки и другие сложные конструктивные элементы также действуют как концентраторы напряжений. Следовательно, помимо определения критического размера дефекта, также важно прогнозировать усталостное поведение деталей с концентрацией напряжений.

Для этого можно использовать простой метод «горячей точки», основанный на максимальном пиковом напряжении у основания надреза. Однако практика показывает, что это слишком консервативно. Чтобы решить эту проблему, Neuber [6] и Peterson [7] предложили линейный метод (LM) и точечный метод (PM) соответственно с идеей, что критический объем материала должен подвергаться критическому напряжению для возникновения усталостного разрушения. Дальнейшее развитие этих методов было проведено Tanaka [8], Lazzarin и соавт. [9]. Taylor описал семейство таких связанных методов как теорию критических расстояний (TCD) [10]. Общей особенностью является использование параметра (критического расстояния), зависящего от материала.

Классическая TCD исходит из предположения о том, что прочность компонентов с надрезом может быть оценена путем анализа поля линейно-упругих напряжений, действующих в окрестности концентратора напряжений. В работе [11] была рассмотрена модификация классической теории критического расстояния на случай упругопластического поведения материала, в результате чего удалось повысить точность прогнозирования. В работах [12; 13] также было показано, что TCD можно использовать для прогнозирования статического разрушения материалов, содержащих различные кон- центраторы напряжений. Более того, в работе [14] продемонстрировано, что теория критических расстояний пригодна для прогнозирования прочности материалов с надрезом, подвергающихся динамическому нагружению.

В настоящее время TCD успешно применяется исследователями для прогнозирования прочности / ресурса широкого спектра различных материалов: металлов, сплавов, композитов, бетона и т.п. [10; 15–17]. Более того, TCD можно комбинировать с различными подходами: например, с критерием плотности энергии деформации [18] и т.д. Однако следует также отметить статьи Lanning et al. [19; 20], Yamashita et al. [21] и Wang et al. [22]. Данные работы сосредоточены на исследовании эффекта размера критического расстояния. При этом отмечаются некоторые проблемы при применении метода к небольшим надрезам и больших значениях коэффициента асимметрии цикла нагружения. В этом случае могут быть использованы некоторые модификации TCD, представленные в работах [10; 23; 24].

Существует ряд различных подходов, которые были приняты для использования TCD для анализа данных экспериментов и для прогнозирования. В принципе, необходимые параметры (критическое расстояние и напряжение) могут быть получены из результатов экспериментов, проведённых только на двух типах образцов, например, на простом образце (без надреза) и образце с надрезом или на двух образцах с разными надрезами.

В обычной TCD критическое расстояние – это параметр материала, который зависит только от коэффициента асимметрии и количества циклов до разрушения. В статье [25] показано, что дефекты, размер которых значительно меньше критического расстояния, можно считать безвредным для рассматриваемого механизма разрушения, но помимо расчетных значений авторы зачастую приводят экспериментальные данные, подтверждающие результаты расчетов, что на практике показывает применимость теории критических расстояний. Таким образом, TCD можно использовать для прогнозирования не только механического поведения тел с концентрацией напряжений, но и для определения критического размера дефекта при различных условиях нагружения. Значения критического расстояния коррелируют с микроструктурой материала, поэтому этот подход, вероятно, можно было бы распространить на композитные материалы с различными ячейками периодичности. Также следует отметить некоторые альтернативные методы: модели «внедренной трещины» и «воображаемой трещины»; подходы, фокусирующиеся на зонах перед трещиной, методы номинального напряжения, методы локального напряженно-деформированного состояния, подходы на основе взвешенных параметров и другие. Более детальные обзоры представлены в работах [30; 31].

Целью данной работы является определение минимальных размеров дефектов, не влияющих на прочностные характеристики изделий из композитного мате- риала СТЭФ, с использованием точечного и линейного подходов TCD.

Материалы, оборудование и результаты установочных экспериментов

В качестве объекта исследования использовался конструкционный слоистый стеклопластик СТЭФ, полученный методом горячего прессования стеклоткани, пропитанной термореактивным связующем на основе комбинированных эпоксидных и фенолформальдегидных смол. Из листа стеклопластика СТЭФ толщиной 5 мм были изготовлены образцы без концентраторов (в виде полосок) и образцы с концентратором в виде V-образного выреза в рабочей части. Эскизы образцов приведены на рис. 1. В качестве образцов с концентраторами напряжений были использованы пять разновидностей с различной геометрией: глубина выреза и радиус вершины выреза – 15 и 5 мм; 15 и 3 мм, 15 и 1 мм; 4 и 1 мм, а также 1 и 1 мм соответственно. Такие разнообразные геометрии вырезов образцов применялись с целью исключения влияния геометрии на определяемые характеристики (значения критических расстояний).

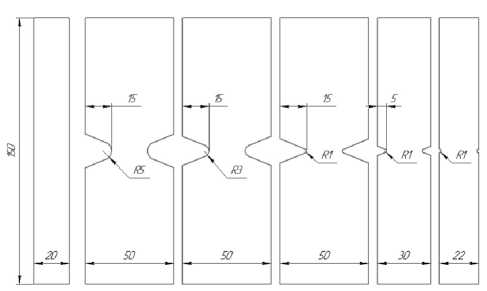
a b с d e f

Рис. 1. Эскиз образцов стеклопластика СТЭФ: полоски ( а ) и V-образные 15×5 ( b ), 15×3 ( c ), 15×1 ( d ), 4×1 ( e ), 1×1 ( f )

Fig. 1. Sketch of STEF fiberglass specimens: strips ( a ) and

V-shaped 15×5 ( b ), 15×3 ( c ), 15×1 ( d ), 4×1 ( e ), 1×1 ( f )

Испытания на одноосное растяжение проводились на универсальной электромеханической испытательной системе Instron 5882 (100кН) совместно с системой анализа полей перемещений и деформаций Vic-3D. В состав видеосистемы входят две цифровые камеры с объективами Limess 2,0/28/0901. Скорость съёмки составляла 15 кадров в секунду с установленным разрешением камер 4,0 Мп. Для всех испытанных образцов материалов скорость нагружения была 2 мм/мин.

По результатам испытаний образцов без концентраторов были получены диаграммы деформирования и нагружения, определены основные механические свойства. По результатам испытаний образцов с V-образным концентратором были получены диаграммы нагружения и определены значения разрушающей нагрузки.

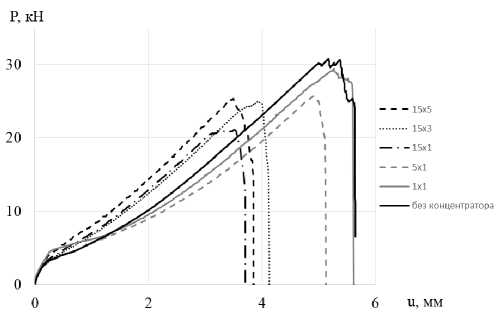
Рис. 2. Диаграммы нагружения образца без концентратора (образец № 1, сплошная черная линия) и образцов с V-образным вырезом в рабочей зоне стеклопластика СТЭФ

Fig. 2. Loading diagrams for specimens without concentrators (a solid black line) and specimens with a V-shaped cut in the working area of STEF fiberglass правлении вдоль оси нагружения. Параметры постобработки были выбраны исходя из ранее проведенных исследований для материала СТЭФ [29].

Таблица 2

Механические характеристики конструкционного стеклопластика СТЭФ

Table 2

Mechanical characteristics of structural fiberglass STEF

Средние значения предела прочности, МПа	Средние значения нагрузки разрушения, кН	Средние значения модуля упругости, ГПа	Среднее значение коэффициента Пуассона
329,6 ± 7,0	30,6 ± 0,4	21,3 ± 0,7	0,200 ± 0,016

Таблица 1

Результаты испытаний образцов стеклопластика СТЭФ на растяжение

Tensile Test Results of STEF Fiberglass specimens

Table 1

№ п/п	Форма образца	Макс. нагрузка, кН	Напряжения при разрушении, МПа
1	Полоска	30,8	330,2
2	Полоска	30,7	339,9
3	Полоска	30,7	330,1
4	Полоска	30,7	327,9
5	Полоска	29,8	319,7
6	V-образный 15×5	25,4	273,7
7	V-образный 15×3	25,1	270,0
8	V-образный 15×1	21,2	223,7
9	V-образный 4×1	25,8	272,8
10	V-образный 1×1	29,5	310,7

На рис. 2 показаны диаграммы нагружения для всех видов образцов стеклопластика СТЭФ. В табл. 1 приведены максимальные значения нагрузок и напряжений. Для образцов с концентратором начальная площадь измерялась в самом узком месте в области выреза. В табл. 2 приведены средние значения основных механических свойств, полученных при испытании 5 образцов полосок (без концентраторов). Статистическая оценка значимости полученных результатов проверялась аналогично данным, представленным в работе [28]. В данной таблице значение коэффициента Пуассона для исследуемого материала приведено из справочных данных.

Для всех образцов стеклопластика с V-образным вырезом была рассмотрена эволюция полей деформаций при нагрузках P′ = 10 кН, P″ = 15 кН, P‴ = 20 кН (рис. 3), также проанализированы поля деформаций ε yy в момент перед разрушением образцов. Деформации в направлении yy соответствуют деформациям в на-

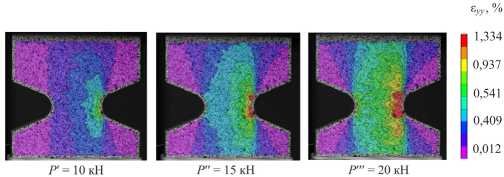
Рис. 3. Поле деформаций ε yy на поверхности образца c V-образным вырезом 15×5 при трех значениях нагрузки

Fig. 3. Fields of deformations ε yy on the surface of a sample with a 15×5 V-notch at 3 load values

Численное моделирование

В рамках комплексного подхода к изучению механического поведения и свойств конструкционного стеклопластика СТЭФ дополнительно проведено численное моделирование процессов деформирования рассматриваемых образцов с использованием метода конечных элементов (МКЭ). Осуществлена серия расчетов на наборе сгущающихся сеток с целью определения сходимости и необходимого числа конечных элементов. Для расчета сходимости использовалась геометрия образца с глубиной выреза 15 мм и радиусом скругления вершины 1 мм. Результаты расчетов представлены на графике (рис. 4). Показано, что порядка 53 000 конечных элементов достаточно для обеспечения сходимости решения задачи. Для определения сходимости была использована модель образца 15×1. При построении конечно-элементной сетки использовались 8-узловые конечные элементы с линейной аппроксимацией.

Для проведения численного моделирования были построены конечно-элементные модели исследуемых образцов с использованием коммерческого программного обеспечения ANSYS Worckbench. На рис. 5 показаны примеры сетки МКЭ, используемой для моделиро- вания образцов с вырезом. При этом была применена мелкая сетка с размером элементов от 0,2 мм в критической области вершины выреза, чтобы обеспечить не менее 5 элементов в пределах критического расстояния. Проведенные численные расчёты на наборе сгущающихся сеток показали, что такого разбиения достаточно для получения точной информации о напряже-нии/расстоянии в критических областях. Также для экономии вычислительных ресурсов и времени расчета области, удаленные от зоны концентраторов, разбивались на более крупные конечные элементы.

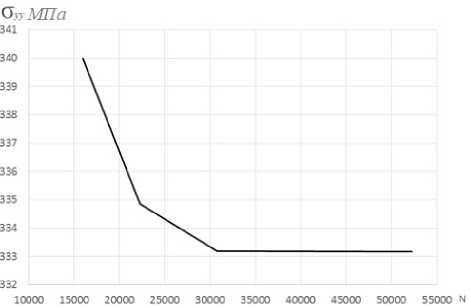
Рис. 4. График сходимости решения численной задачи

Fig. 4. Graph of the convergence of the solution of a numerical solution

Рис. 5. Пример конечно-элементной сетки компьютерных моделей образцов

Fig. 5. Example of finite element mesh of computer models of specimens

Свойства материала при численных расчетах задавались согласно данным, полученным из установочных квазистатических экспериментов на растяжение образов в виде полосок без концентраторов напряжений. Так, модуль упругости принят равным 21,3 ГПа, коэффициент Пуассона 0.2. Один из краёв образца жестко закреплен, а к другому краю была приложена нагрузка вдоль оси образца.

Свойства композита изучались только в одном направлении (направлении нагружения), поэтому материал при расчете задан изотропным. Как показывает практика, подобное допущение может применяться при ис- пользовании TCD, не оказывая существенного влияния на результат. Так, например, в работах [34; 35] схожая методика была использована при моделировании усталостного поведения титанового сплава на образцах, напечатанных на 3D-принтере в горизонтальном направлении.

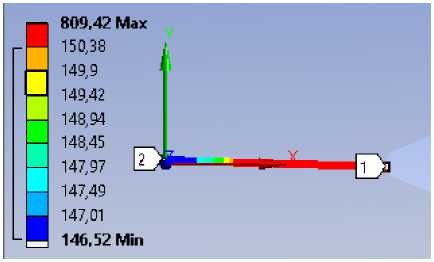
На рис. 6 показан пример расчёта МКЭ для образца с вырезом с радиусом основания 1 мм. Выведены поля максимальных главных напряжений. При реализации TCD линеаризованное максимальное главное напряжение (рис. 6, b ) было записано как функция напряжений, зависящих от расстояния от вершины выреза вдоль средней линии образца (кривая зависимости напряжения от расстояния σ( r )). На рис. 6, b , приведены линеаризованные максимальные главные напряжения для всех типов образцов.

b

Рис. 6. Результаты расчёта МКЭ для образца с вырезом с радиусом основания 1 мм: a – контуры максимального главного напряжения в МПа; b – линеаризованное максимальное главное напряжение в МПа

Fig. 6. The results of the FEM calculation for a sample with a cutout with a base radius of 1 mm: a – Contours of the maximum principal stress in MPa; b – linearized maximum principal stress in MPa

В табл. 3 представлено сравнение полей деформаций, полученных с использованием видеосистемы Vic3D непосредственно во время эксперимента, и результатов численных расчетов в Ansys Worckbench при значении нагрузки, равной 15кН, соответствующей упругому участку диаграммы деформирования.

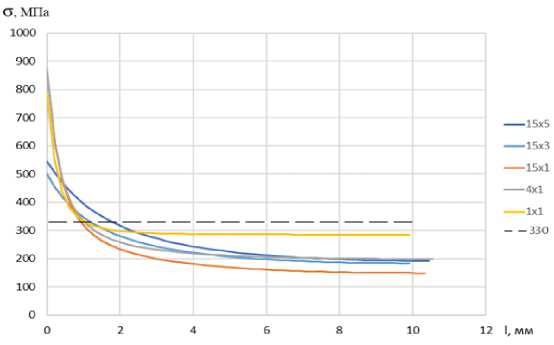
Рис. 7. Линеаризованные максимальные главные напряжения в МПа для образцов с V-образными вырезами 15×5, 15×3, 15×1, 4×1, 1×1. Пунктирной линией обозначен уровень напряжений, соответствующий пределу прочности образцов без концентраторов (полоска)

Таблица 3

Отклонения максимальных значений полей деформации численного расчета от значений, полученных системой Vic-3D

Table 3

Deviations of the maximum values of the deformation fields of the numerical calculation from the values obtained by the Vic-3D system

Образец	Отклонение, %
V-образный 15×5	7,4
V-образный 15×3	5,8
V-образный 15×1	14,1
V-образный 4×1	13,0
V-образный 1×1	12,3

Оценка прочности на основе TCD

Fig. 7. Linearized maximum principal stresses in MPa for V-shaped specimens 15×5, 15×3, 15×1, 4×1, 1×1. The dotted line indicates the stress level corresponding to the ultimate strength of specimens without concentrators (strip)

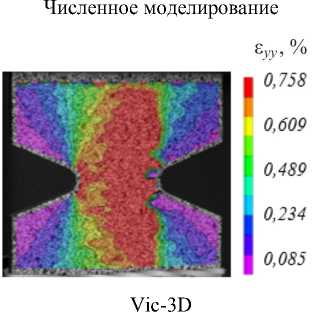
Рис. 8. Сравнение полей деформаций ε yy , полученных с использованием численного моделирования  (слева)

видеосистемы Vic-3D (справа) для образца 15×5

Fig. 8. Comparison of strain fields ε yy obtained using numerical simulation (left) Vic-3D video system (right) for specimen 15×5

Теория критических расстояний представляет собой подход линейной упругой механики разрушения и основана на анализе упругих напряжений в окрестности выреза. Учитывается напряжение в характеристической точке или среднее напряжение по характеристической линии вблизи выреза. Прогнозируется, что разрушение происходит, когда значение напряжений в точке или усредненное по линии превышает предел прочности образца без концентратора, а критическое расстояние для материала и соответственно допустимый размер дефекта не превышают значение, полученное по формулам (1) и (2) (табл. 4). При этом анализируется два типа образцов: с концентратором и без концентратора. По типу топологии подход можно разделить на категории, как показано на рис. 9.

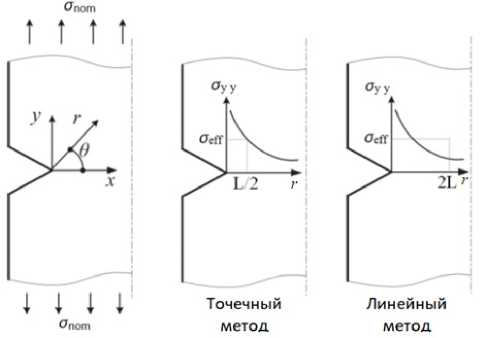
Рис. 9. Линейный и точечный метод теории критических расстояний

Fig. 9. Linear and point method of the theory of critical distances

Точечный метод:

Для оценки полученных результатов вычислена процентная доля отклонения численного решения от результатов, полученных при использовании видеосистемы контроля деформаций. В табл. 3 представлены данные по каждому образцу.

σ eff = σ 0 = σ yy (Ɵ = 0, r = L /2).            (1)

Линейный метод:

1 2L

° eff = С0 = 2^ J ° XV (9 = 0, r ) dr,           (2)

где σ y ( r ) – функция напряжения от расстояния от вершины выреза образца; σ 0 – предел прочности образца полоски; L – критическое расстояние.

Учитывая кривую σ y ( r ) (см. рис. 6) и соответствующий предел прочности образца полоски без выреза, два значения L были рассчитаны в соответствии с PM и LM (табл. 5).

Таблица 4

Значения критических расстояний по точечному и линейному методам для конструкционного стеклопластика СТЭФ

Table 4

Values of critical distances by point and linear methods for STEF structural fiberglass

№ п/п	Отношение макс. нагр. к площ. минимал. сечения, МПа	Критическое расстояние по точечному методу, мм	Критическое расстояние по линейному методу, мм	Коэффициент концентрации напряжений	Образец
1	273,7	3,64	2,29	2,00	V-образ. 15×5
2	270,0	2,46	1,50	1,86	V-образ. 15×3
3	223,7	1,89	1,47	3,84	V-образ. 15×1
4	272,8	2,10	1,75	3,21	V-образ. 4×1
5	310,7	2,17	2,51	2,53	V-образ. 1×1
Среднее значение		2,45	1,90
Среднеквадратичное отклонение		0,69	0,47
Коэффициент вариации, %		28	25

Далее для оценки точности метода средние значения были использованы для прогнозирования предельных напряжений для образцов с концентраторами напряжений.

Ошибка подходов определялась по формуле

G„ -

ME = --- . 100 %,            (3)

σ max где σmax/pr – прогнозируемое значения предельного напряжения для образца с концентратором, σmax – предельное значение напряжения для образца с концентратором, полученное в эксперименте.

Из результатов, представленных в табл. 4.2, можно увидеть, что ошибка прогноза варьируется от –12,1 до 13,1 % для точечного метода и от –5,1 до 10,4 % для линейного метода. В целом видно, что линейный метод более точен, чем точечный. При этом оба метода демонстрируют достаточно хорошую точность предсказания. По теории критических расстояний погрешность менее 20 % (10 % – ошибка эксперимента, 10 % – ошибка моделирования) считается удовлетворительной.

Как уже отмечалось ранее, если длина дефекта значительно меньше критического расстояния, то дефект можно считать безвредным.

Таблица 5

Ошибки прогнозирования согласно точечного и линейного методов для конструкционного стеклопластика СТЭФ

Table 5

Predicting errors according to point and linear methods for STEF structural fiberglass

№ п/п	Ошибка по точечному методу ME, %	Ошибка по линейному методу ME, %	Коэффициент концентрации напряжений	Образец
1	-12,1	-5,1	2,00	V-образ. 15×5
2	-0,1	6,4	1,86	V-образ. 15×3
3	13,1	10,4	3,84	V-образ. 15×1
4	6,6	2,6	3,21	V-образ. 4×1
5	2,8	-3,8	2,53	V-образ. 1×1

В данной работе для образца с вырезом глубиной 1 мм точеный метод прогнозирует напряжение разрушения 323 МПа, в то время как линейный метод примерно 305 МПа. При сравнении данных значений с пределом прочности для образцов полосок (без концентраторов) падение предельных нагрузок составляет примерно 2 и 8 % при значениях критических расстояний 2,45 и 1,90 мм соответственно. Другими словами, если длина выреза, скола или дефекта меньше в 2,45 раза, чем критическое расстояние, то это приводит к падению предельной нагрузки на 2 %, а если в 1,9 раза, то на 8 %. Таким образом, можно сделать вывод, что дефект длиной меньше критического расстояния в 2–3 раза приводит к несущественному падению предельной нагрузки при растяжении.

Заключение

Проведено комплексное исследование механических свойств и поведения композитных материалов (конструкционный стеклопластик СТЭФ). В рамках исследования выполнены работы по проведению квази-статических испытаний на растяжение образцов в виде полосок (для определения механических свойств) и образцов с концентраторами напряжений (вырезы различной конфигурации), работы по численному моделированию, используемых образцов, а также анализ свойств исследуемого материала по теории критических расстояний.

Из результатов, представленных в табл. 5, можно увидеть, что ошибка прогноза варьируется от –12,1 до 13,1 % для точечного метода и от –5,1 до 10,4 % для линейного метода. В целом видно, что линейный метод более точен, чем точечный. При этом оба метода демонстрируют достаточно хорошую точность предсказания.

Согласно теории критических расстояний, если длина дефекта значительно меньше критического расстояния, то дефект можно считать безвредным. Для конструкционного стеклопластика СТЭФ дефекты