Определение параметров эксплуатационной надежности элементов систем управления уличного освещения

Введение 1

Многофункциональные, или сложные систе-мы в силу динамики структуры и разнообразия выполняемых задач могут функционировать с раз-ными уровнями качества. В таких системах появ-ление отказов отдельных элементов приводит не к полному выходу системы из строя, а лишь к не ко -торому ухудшению качества функционирования и снижению эффективности системы в целом [1].

Оптимизация эксплуатационной надежности

Для оптимизации надежности СИС и СУ применяется математический аппарат теории на-дежности и теории оптимального управления. За критерий качества функционирования сложной АСУ принимается эффективность функциониро-вания, характеризующая возможность выполнения сложной АСУ тех или иных частных задач. Эф-фективность функционирования в общем виде оценивается выражением

n

E ( t )       P ( Hi ) ф i .                           (1)

i 1

Каждое состояние Hi СИС характеризуется выходным эффектом Ф i , вероятность нахождения изделия в этом состоянии измеряется величиной Р ( Нi ) . ВеличиныФ i и H_i независимы.

Задача оценки количественных характеристик надежности и эффективности носит существенно вероятностный характер, поэтому приемлемым методом исследования является метод статистиче-ских исследований (например, метод Монте-Карло). Сущность последнего состоит в моделиро-вании случайного процесса путем выбора по жре-бию отдельных реализаций процесса.

Для определения выходных эффектов Ф i наи ^-более целесообразна экспериментальная проверка функционирования изделий, во время которой ис-следуется влияние отказов отдельных элементов изделия на его выходной эффект.

Задача исследования эффективности функ-ционирования СИС в процессе разработки сводит-ся к оптимальному проектированию, осуществ-ляемому с позиции теории оптимального управле-ния [2‒5]. В этом случае эффективность функцио-нирования (1) принимается за критерий оптималь-

ности (                   ),-

. -

(Н i)-

,-

-

-

,-

Предположим,                    n = 18- делий (-

: 2- ния, 2, радиатора),                            Hi-

2 ⁿ . -

, N        ( N < n ). -

• 6 , , R

(R = 6.).

R

Pj xj     R 1 1 Pig xig ,(2)

g 1

где Pig ‒                                         i--

,                  g -       ( g = 1÷ R );

xig ‒                              ,                         i--

ЛИЯ g-.

Каждое m--

-

: N

Pm =П[ajmPj +(1 ajm 1 Pj  ,(3)

g 1

jm ‒             j-           m-- темы (ajm = 0…1).

, ,                                               ,-

,- мыми,.

- р 2N

E(t)=11P Pm фm .(4)

Т]=1m 1 ,- m--

.

-

:

р 2 ^N

EE=££P P_m ф m => max; mm

П- 1 m 1

nN

C ^{( 0      n} c_ix_i    ^N cixi ;

i 1 j 1

77 = 1, р ; m 1,2 ^N ; i 1, n ; j 1, N 1

:

• 1),

,-

‒ , ;

• 2)                                  xi ‒-

• ‒-
• ;

{ x_i m _{_} in      1              ,                          x_i max 2 -

.

дифференцируемая,- градиента,-

:

nE

А E = 2^А x_i => max ,

i i1оxi i ‒                                         .

.

точку x ⁰

f =Е ( x ).

- xk 1 xk hk Vf(xk), где k ‒                 k = 0, 1, …; hk ‒ шага ; f(xk) ‒                       f (x)          xk ,

V f ( x^k )

f ( x^k ) _, f ( x^k ) x ₂        x ₃

f ( x^k ) 1 с x_n J

h0

0,1.                                           0,0001.

-

:

V f ( x^k )II <Е.

Для определения координат вектора градиен-та V f ( x^k ) использовалась разностная формула f ( x^k )

x ₁ .

f ( x 1 ^k , x 2 ^k , , xi^k + xi^k , , xn^k ) f ( x 1 ^k , x 2 ^k , , xi^k , , xn^k )

Д x

Относительный шаг дифференцирования при-нят равным А x_i^k =0,0001.

Полученные коэффициенты приводят к удо-рожанию системы автоматического регулирования системой уличного освещения почти в 2 раза.

С использованием метода неопределенных множителей Лагранжа при решении задачи нахо-ждения максимума целевой функции учитываются ограничения на удорожание элементов системы автоматического регулирования системы уличного освещения.

Экстремум целевой функции лежит на плос-кости ограничения, поэтому как выбор начальной точки движения х 0, так и самодвижение по гради-енту целесообразнее всего в условиях данной за-дачи осуществлять в плоскости ограничения. Та-ким образом, на движение по градиенту, точнее на приращение переменных {Д x_i }, в рассматривав-мой задаче накладываются следующие ограниче-:

ⁿ c_i x_i 0;

i 1

n

Е(^д x_i ) 2 _L 2_.

i 1

Первое ограничение в системе (6) определяет условие движения в плоскости ограничения, вто -рое ‒ заданную длину вектора приращений, обес-печивающую нахождение в границах плоскости ограничений.

Для нахождения приращения независимых переменных {Дxi } целесообразно использовать метод неопределенных множителей Лагранжа, согласно которому предварительно составляется вспомогательная функция n                     n

^F (^дx_i     ^{n E} x_i U1 ⁿ   x_i ) 2 _L 2

i 1 xi                     i 1

n

-X 2 У, c_i (А x_i )^, i 1

где второй член является формальной функцией связи , aX ₁и X 2 ‒ неопределенные множители Лагранжа. Затем составляется система уравнений :

F(Дxi ) сE         х—*

i E2X1 (А xi Н c (i 1,n).(7)

5(Дxi )    с xii i

Умножая каждое из уравнений системы (7) на ci и суммируя все уравнения, получаем с учетом первого ограничения из системы (6) следующее :

/1

nn

X2 n ci2

i1

E ci       .

xi

Перенося в каждом из уравнений системы (7)

2X1 (дxi ) в левую часть, возводя в квадрат обе части и суммируя все уравнения, получаем с уче-том второго ограничения из системы (6) следую-:

X 1

nE г^х i 1     xi

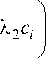
Из системы уравнений (7) получаем также

1 E

Дxi =--- -X i2

²X1 x_i

-X₂ c_i

n

E

_, I ^ E  А II ^| СE

L --X 2ci|у i 1 xi

² ( i 1, n ). (8)

9 xi

Система уравнений (8) позволяет определить приращения независимых переменных {Дxi } ДЛЯ движения по градиенту в плоскости ограничения. Значение длины L вектора приращений градиента Е в системе (8), при котором E -> max , определя-ется с помощью правила «золотого сечения».

На первом этапе вводим в ЭВМ исходную информацию . Информация о количестве перемен-ных и , количестве узлов N, числе информацион-ных каналов G , ограничивающей общей стоимости С (0) и точности определения вектора прир ятл ений 8 = 0,01 вводится в виде чисел. Информация о выходных эффектах работоспособных каналов Ф m , стоимости изделий (ПСУ и СА) c_i и узлов C_j =у c_i , вероятностях безотказной работы уз-лов { p_j (x_j )} , матрица изделий (ПСУ и СА) АХ и матрица каналов АК вводятся в виде массивов.

:

_X л о!у

X 0       x 0 i .

Затем осуществлено движение вдоль поверх- n

Г \       , _г(0)

ности ограничения C      cixi C i1 наискорейшего спуска.

Улучшения и резервирование ведут к удоро-жанию пропорционально кратности произведен-:

C( xi ) =cixi, где ci ‒ стоимость нерезервированных ПСУ и СА в l-м канале .

Поэтому естественно в качестве функции штрафа для решения задачи оптимизации структу- ры сложной АСУ использовать выражение n

_Cⁿ        _C (0 )

C       cixiC, i1

где C ⁰ ‒ допустимая стоимость улучшения АСУ, являющаяся плоскостью ограничения штрафной функции.

Определяем переменные, для которых А x_i 0 , т.е. переменные , не получающие прира-щения. Допустимое значение длины вектора при-ращений

n

• ⁿ x_i ), i 1

т.е. такое значение L , при котором вектор, соот-ветствующий направлению наискорейшего спуска, не выходит за пределы фазового пространства x _{0 n} 1 x _{0 n} 2 . Это значение определяется как оптимальное из всех значений длин Li , найденных по переменным {Д x_i }, для которых А x_i * 0.Затем определяем поиск экстремума целевой функции в локальной области по правилу «золотого сечения», ибо в области локального экстремума возможен одномерный оптимальный поиск, что ускоряет решение задачи оптимизации. Делим отрезок AB = (0, L _min) с помощью правила «золотого се-чения» на отрезки L ₁ и L ₂, определяет соответст-вующие значения переменных x 1 i и x 2 i и функ ^-ции E ₁ и E ₂, вычисленные в точках x _{1 i} и x _{2 i} .

Логически сравниваем значения функций E 1 и E ₂ . Если E ₂ >  E ₁ , то отбрасывается отрезок, лежа-щий левее точки L ₁ , и в качестве крайней левой точки отрезка, на котором разыскивается максимум функции E , берется значение А = L ₁ . Если E 2 <  E 1, то отбрасывается отрезок, лежащий правее точки В , принимается В = L ₂ . Процедура продолжается до тех пор, пока уменьшающийся отрезок АВ не ста-нет меньше заданной величины s .

После этого окончательное значение длины L вектора градиента определяется как середина от-резка АВ и находится вектор X _{2 i} °{x _{2 i} }^, соот ^-ветствующий этому значению L.

Если L >Е, то производится дальнейшее дви-жение по градиенту функции Е в плоскости огра-ничения. Если L< Е, то предполагается, что точка локального максимума целевой функции достиг-нута. Поэтому вычисляем целевую функцию в найденной точке и выводим на печать значения max И xi_ опт .

Программа оптимизации структуры сложной АСУ по критерию эффективности функциониро-вания при ограничении по стоимости реализована на языке C++Builder.

Полученные коэффициенты приводят к удо-рожанию изделий системы автоматического регу-лирования системы уличного освещения :        - ков питания в 1,5189 раза, блоков регулирования в 1,015 раза, светодиодной матрицы в 1,505 раза, радиатора в 2,01 раза.

Следовательно , возможно увеличивать в ис-пользуемых в системе автоматизации светодиод-ных источников света массу радиатора в 2 раза и усовершенствовать импульсные источники пита-ния путем замены конденсаторов на более надеж-ные с удорожанием источника в 1,589 раза [5].

Заключение

Аналитические методы и методы вычисли-тельного моделирования, применяемые для расче-та и анализа показателей надежности элементов и системы автоматизации, могут быть применены для установления эффективности функционирова-ния сложных АСУ. Данная методика рекомендует-ся к применению в реальных автоматизированных системах управления наружным освещением.