Определение параметров электродинамической космической тросовой системы в задаче уборки космического мусора

С начала космической деятельности человечества количество техногенных объектов в космосе постоянно растет. В их число входят как функционирующие аппараты, так и вышедшие из строя спутники, верхние ступени ракет, различные мелкие обломки, называемые в научной литературе космическим мусором. Их взаимные столкновения могут вызвать эффект Кесслера [1], который заключается в том, что в результате лавинообразного роста числа обломков вывод новых космических аппаратов на орбиту станет невозможен. Поэтому уборка космического мусора является актуальной и важной научнотехнической задачей.

Существуют проекты, предполагающие: увод тел с орбиты с помощью импульсных лазеров [2] активных космических аппаратов, захватывающих нефункционирующий спускаемый объект с помощью троса [3-5], электродинамических тросовых систем [6], в частности стоит отметить проект, который предложил R. P. Hoyt [7]. В представленных проектах электродинамический трос изначально устанавливался на космический аппарат (КА) и разворачивался после завершения программы полета. Рассмотрим альтернативную схему, состоящую из малого КА с тросовой системой на борту, который подлетает к нефункционирующему объекту, соединяется с ним гарпуном и разворачивает трос. После этого по тросу пускается ток и, благодаря взаимодействию с магнитным полем Земли, в нем возникает сила

Ампера, направленная перпендикулярно тросу. Эту силу можно использовать для торможения космической тросовой системы (КТС) и увода с орбиты нефункционирующего объекта.

Целью работы является разработка математической модели электродинамической КТС и исследование влияния величины силы тока и длины троса на время увода нефункционирующего космического объекта с орбиты.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ЭЛЕКТРОДИНАМИЧЕСКОЙ ТРОСОВОЙ

СИСТЕМЫ

Рассмотрим КТС, состоящую из КА, невесомого упругого троса и нефункционирующего объекта. КА и нефункционирующий объект представим, как материальные точки A и B соответственно (рис. 1). Будем исследовать плоское движение системы и считать, что движение происходит в плоскости экватора. Состояние

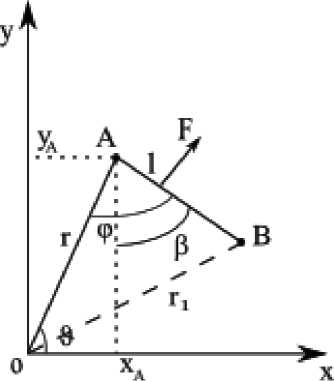
Рис. 1. Космическая тросовая система механической системы определяется четырьмя обобщенными координатами: r – расстоянием

от Земли до точки A , 1 - длиной троса, Э - углом истинной аномалии КА и ф - углом отклонения троса от местной вертикали.

дикулярен плоскости рис. 1. В этом случае модуль силы Ампера находится, как

F _ BI1

Составим уравнение движения КТС, восполь-

зовавшись формализмом Лагранжа [8]:

d (dL_ }_(L_ _ Q dt v 5qi y 5 qi     1 ’ где L _ T - P - Лагранжиан системы,

T и

Обобщенные силы найдем по формуле [8]: 5 A

^Q i ^_ ^,      q i ^{_ (} r , Ф , ^{1 , S )} ,       (6)

5Qi где 5q - виртуальное перемещение i-ой обобщённой координаты, 5A - элементарная работа.

Запишем элементарную работу 5 A

P кинетическая и потенциальная энергия, Q _ ( Q ф ,Q r , Q _s ,Q i ) -обобщенные силы.

Кинетическая энергия системы имеет вид:

t _ m A V ₊ m B VL ,       (2)

где m_A , m_B – масса КА и нефункционирующий объект, V A _ r A , V_B _ r B ; V A , V_B - абсолютные скорости, r _A , r _B - радиус-вектора точек A и B

5 A _ 5 rF _ F_x ( 5 r cos S + r ( - sin S ) 5S + ^{5 1} sin в + - 5в cos в ) +

2       2            (7)

+ F y ( 5 r sin S + r 5S cos S - у cos в + 2 5в sin в )

соответственно:

( r cos S )       ( r cos S + 1 sin в )

^r a =    'o’ r B =

( r Sin S )      ( r sin S - 1 cos в )

Подставляя (7)в (6) , получаем:

5 A

Q_T _ — _ cos S ( F cos в ) + sin S ( F sin в ).

r 5 r

Q s _ l A _- ^Fr cos Ф + F1 . Q ф _ l A _ ^FA •

5S                    оф 2

5 A

_ 5 1F cos — _ 0. 2

П где в _ ф---+ S (рис. 1). Подставляя (3) в (2), 2

получим выражение для кинетической энергии:

T _ m A (( r cos S )² + ( r sin S )²) +

+ m_B (( r cos Э + 1 sin в )² + ( r sin Э - 1 cos в )²

.

Потенциальная энергия системы складывается из энергий гравитационных воздействий и упругого воздействия, обусловленного наличием троса.

P __^_^ + c ( 1 _ 1 o ) ,   (5)

r_Ar_B 2

где н - гравитационный параметр, 1 ₀ - длина троса в недеформируемом состоянии, c – жесткость троса.

Используя (4)и (5), запишем Лагранжиан системы:

L _ m A (( r cos S ) + ( r sin S )²) +

=            2

В случае, когда сила тока не изменяется в процессе движения, она все время перпендикулярна тросу и создает момент, стремящийся повернуть тросовую систему относительно ее центра масс. На половине оборота тросовой системы сила направлена противоположно направлению орбитального движения и тормозит КТС, а на половине - по направлению орбитального движения и разгоняет ее. Для того, чтобы обеспечить эффективное торможение КТС нужно исключить этап ее разгона. Это можно сделать, изменив направление тока в тросе на противоположное. В этом случае сила Ампера все время будет направлена против противоположного направления движения системы и будет тормозить. Указанное поведение может быть реализовано при использовании закона управления

F _ BI1 sign(cos ф )

m_B (( r cos S + 1 sin( ф - ^П + S ))² + ( r sin S - 1 cos( ф - ^П + Э ))²

ЧИСЛЕННЫЙ ЭКСПЕРИМЕНТ

-

H m A

r

-

^ m B- + ^C ( 1 - 1 o ) ^r 1      ²

Помимо потенциальных сил упругости и натяжения троса на систему действует непотенциальная сила Ампера:

F _ B x 1 1 ,

где B - вектор магнитной индукции, I - вектор силы тока. В случае использования модели прямого диполя [9] вектор магнитной индукции направлен вдоль оси вращения Земли и перпен-

Рассмотрим движение КТС, имеющей следующие параметры: m_A = 150 кг, m_B = 1500 кг. Исследуем влияние длины троса и модуля силы тока на время спуска нефункционирующего объекта с орбиты. Будем считать, что: I е [1,3.5] А, 1 е [5000, 15000] км. С помощью системы (1) проведем серию численных расчетов. На рис. 2 показана зависимость силы тока от времени спуска с орбиты для КТС с разной длиной троса. Видно, что при увеличении длины троса и силы тока время спуска нефункционирующего объекта уменьшается.

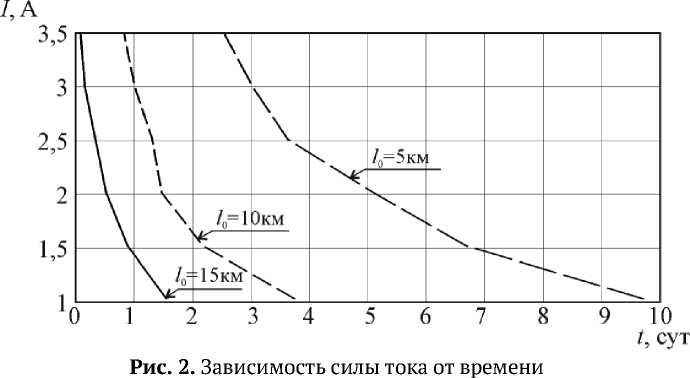
ЗАКЛЮЧЕНИЕ

На основе формализма Лагранжа построена математическая модель, учитывающая взаи- 3 модействие проводящего троса с магнитным . полем Земли, и предложен закон управлением силой тока, обеспечивающий увод нефункционирующего объекта с орбиты. С помощью раз- 4. работанной модели проведена серия численных экспериментов, в ходе которой установлено, что при увеличении длины троса и силы тока время 5. увода нефункционирующего космического объекта с орбиты уменьшается.

Представленные результаты получены в рамках выполнения государственного задания Минобрнауки России №9.540.2014/К.