Определение параметров корректирующего устройства для системы четвертого порядка, оптимальной по быстродействию

Синтез систем высокого порядка можно проводить с помощью методики, описанной в [1], где рассмотрен стабилизатор напряжения с двухзвенным фильтром, описываемый дифференциальным уравнением четвертого порядка. Методика синтеза оптимальных по быстродействию систем высокого порядка состоит из трех основных этапов: первый этап - определение описания гиперповерхности переключения; второй этап - аппроксимация поверхности; третий этап - формирование коррекции.

На первом этапе находят описание поверхности переключения 5( e ) в виде набора точек в n-мерном фазовом пространстве координат ошибки и ее производных. Это можно сделать, решив систему дифференциальных уравнений, используя принцип обратного времени. На втором этапе по имеющимся точкам поверхности и заданному выражению для аппроксимации необходимо получить аналитическое выражение поверхности 5( e ). На третьем этапе рассматривают аналитическое выражение 5( e ), определяющее передаточную функцию устройства управления. В данной статье мы остановимся на последнем этапе.

На данном этапе методики [1], базирующейся на методе фазовых траекторий, формируется уравнение гиперповерхности переключения в координатах сигнала ошибки и ее производных в общем виде имеется выражение:

n - 1

X a i e = 0, (1) i = 0

где x. - координаты ошибки; a. - коэффициенты, полученные на втором этапе методики [1], с помощью метода наименьших квадратов.

Применительно к системе четвертого порядка получим следующее выражение:

a ₀е₀ + a 1 s 1 + a ₂s 2 + a ₃s₃ = 0, (2) где e ₀, e ₁, e ₂, e ₃ - координаты ошибки, ее первой, второй и третьей производных; a₀, a^ a₂, a₃ - коэффициенты. Коэффициент a₀ удобно принять равным единице и пересчитать остальные коэффициенты.

Уравнение (2) определяет передаточную функцию устройства управления. Такой гиперповерхности переключения соответствует звено коррекции с передаточной функцией:

W_k ( p ) = a 3 • p ³ + a 2 • p ² + a 1 • p + 1. (3)

Поскольку гиперповерхность переключения задана в координатах сигнала ошибки, то корректирующее устройство исправляет в системе сигнал ошибки (рис. 1).

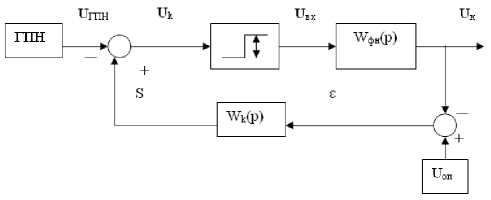
Рис. 1. Структурная схема стабилизатора с коррекцией: e - сигнал ошибки; 5 - сигнал с корректирующего устройства; U - пилообразный сигнал с генератора пилообразного напряжения; U_k - напряжение на ключ; С_вх - управляющее напряжение; U_n - напряжение нагрузки; U - опорное напряжение

Передаточная функция звена коррекции (3) заставляет систему работать нужным образом лишь теоретически. Но на практике реализация передаточной функции только третьего порядка в числителе не применяется из-за того, что в реальной системе всегда присутствуют различные сигналы шума.

В большинстве случаев сигнал шума - это сигнал с маленькой амплитудой, но с очень большой частотой. Его можно описать следующим выражением:

U _ш = A n sin( w _ш t ), (4) где U - сигнал шума, В; Л - амплитуда сигнала шума, В; w_ш - частота сигнала шума, Гц; t - время, с.

Амплитуда сигнала шума Л_ш мала: Л_ш = 10 ⁹ В, в то время как его частота w очень велика: w = 10⁹ В.

Сигнал ошибки е будет складываться из суммы полезного сигнала и сигнала шума:

s = U „ + U ш ,                    (5)

где U - полезный сигнал, В.

Если осуществить в системе реализацию корректирующего устройства с передаточной функцией только третьего порядка в числителе, то сигнал ошибки будет продифференцирован три раза:

^s ' = U п ” ⁺ 4 п ^w ш ^COs( w n t ^{), (6)} где s ' - производная сигнала ошибки; U' - производная полезного сигнала; U Ш - производная сигнала шума.

После нахождения уже первой производной сигнала ошибки амплитуда помех значительно возрастает - примерно до 1 В.

Для второй и третьей производной сигнала ошибки имеем следующие выражения:

^S ” = ^U П ⁺ A n w ш w ш ^sin( w n t ^{),            (7)}

^s* = U П"+ A n w ш W n w _mcos ⁽ W n t X          ⁽8⁾

где s' - вторая производная сигнала ошибки; U П - вторая производная полезного сигнала; U Ш - вторая производная сигнала шума; s" - третья производная сигнала ошибки; U” - третья производная полезного сигнала; U _ш - третья производная сигнала шума.

По выражению (8) следует, что в системе в значительной степени увеличилась амплитуда сигнала шума.

Таким образом, при дифференцировании сигнала шума из-за его высокой частоты уровень его сигнала ста новится соизмеримым с полезным сигналом, что в итоге приводит к неработоспособности системы в целом.

Для преодоления этого недостатка необходимо изменить корректирующую передаточную функцию, чтобы исключить дифференцирование на высоких частотах, при этом оставив дифференцирование для частот, которые определяют основной переходной процесс. Поэтому реализуем звено коррекции с передаточной функцией:

W k ⁽ Р ) =

a 3 • p ³ + a 2 • p ² + а 1 • p + 1 b₃ • p ³ + b ₂ • p ² + b 1 • p + 1

Это интегрально-дифференциальное звено третьего порядка в числителе и знаменателе, и как необходимо подобрать коэффициенты Ь_З, Ь₂, Ь₁ в знаменателе. Для этого выполним следующие действия:

• 1.    Вычислим специальный коэффициент для числителя. Возьмем коэффициент а_З и извлечем из него кубический корень:

• 2.    Выберем специальный коэффициент знаменателя

a 3 _T = 3[а 3 , (10)

где аЗ _г - специальный коэффициент числителя.

меньше минимум в тридцать раз:

b 3_Т =    a ³ T ,

^T   30...100

где ЬЗ _Г - специальный коэффициент знаменателя.

• З.    Пусть знаменатель состоит из трех звеньев первого порядка

( b 3 _Tp + 1)( b 3 _Tp + 1)( b 3 _Tp + 1).           (12)

Перемножим скобки и получим полином в знаменателе:

b ₃ • p ³ + b ₂ • p ² + b 1 • p + 1.               (1З)

Сравнение звеньев с передаточной функцией (З) и (9) в общем виде можно представить графически (рис. 2).

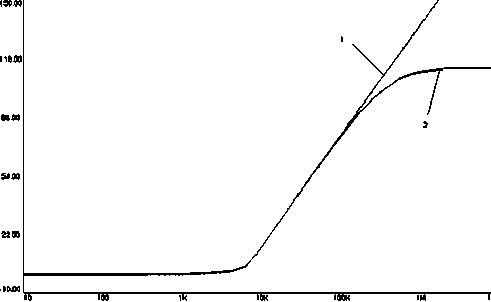
Рис. 2. Логарифмические амплитудно-частотные характеристики звеньев: 1 - с передаточной функцией (З);

2 - с передаточной функцией (З)

Таким образом, нами была сформирована передаточная функция звена коррекции, фильтрующая помехи на высоких частотах и придающая системе оптимальность по быстродействию. Формирование знаменателя в виде полинома, который можно представить из трех последо вательно соединенных звеньев первого порядка, значительно упрощает практическую реализацию корректирующего звена, например, на операционных усилителях.

Покажем, что указанное соотношение специальных коэффициентов числителя и знаменателя верно. Для этого рассмотрим пример, данный в [1], и будем варьировать соотношение коэффициентов.

Передаточная функция объекта управления

W ^{0У (} p ) = 1,540 " ¹⁷ • p ⁴ + 5,930 '■ • p ³ + 4,503 • 10 ^{- 8} • p² + 1,135 • 10 ^{- 4} • p + 15,03' ⁽¹⁴⁾

Общий вид звена коррекции в рассматриваемом примере следующий:

2,705 -W¹⁴ • p ³ + 2,704 - 10 " ⁹ • p ² + 9,00640 • p + 1

W oy ^{( p} ) =                   J 3 J 2 J 1                 • ⁽¹⁵⁾

b ₃ • p ³ + b ₂ • p ² + b • p + 1

Выберем разные варианты знаменателя звена коррекции. Известно, что для системы второго порядка, оптимальной по быстродействию, специальные коэффициенты числителя и знаменателя отличаются в 10...20 раз [2]. Поэтому начнем именно с этого соотношения.

Сформируем звенья коррекции для различных соотношений специальных коэффициентов:

а 3 _T = W ₍ ) = 2,705•Ю ^{- 14} • p ³ + 2,704•Ю ^{- 9} • p² + 9,006 • 10 ^{- 5} • p + 1

• ¹⁾    b 3 _T~ ’ ^k p ~3,382 • 10 ^{- 18} • p ³ + 6,759 •Ю ^{- 12} • p² + 4,503 •Ю ^{- 6} • p + 1;

а 3 _T =              2,705•Ю ^{- 14} • p ³ + 2,70440 9 • p ² + 9,00640 • p + 1

• ²⁾    b 3 _T ’ ^{k ( p} ) = 1,003 • 10 ^{- 18} • p ³ + 3,006 40 ^{- 12} • p ² + 3,003•Ю ^{- 6} • p + 1;

а 3 _T = W ₍ ) = 2,705•Ю ^{- 14} • p ³ + 2,70440 9 • p² + 9,006 40 • p + 1

• ^З)    b 3 _T~ ’ ^{k (} p ) = 1,252 •Ю ^{- 19} • p ³ + 7,509 •Ю ^{- 13} • p ² + 1,501 • 10 ^{- 6} • p + 1;

• ., а 3 T = ₁₀₀ W ₍ ) = 2,705 • 10 ^{- 14} • p³ + 2,70440 ^{- 9} • p ² + 9,00640 ^{- 5} • p + 1

V b 3 _T       ’ ^k( p 2,70540 ^{- 20} • p ³ + 2,70440 ^{- 13} • p ² + 9,006 • 10 ^- 7 • p + 1;

• , а 3 _T = 150 W 2,705 • 10 ^{- 14} • p ³ + 2,704 • 10 ^{- 9} • p ² + 9,006 • 10 ^- 5 • p + 1

• ⁵⁾ b 3 _T”    ’ ^k ( ^p ) = 8,012 • 10 ^{- 21} • p ³ + 1,201 • 10 ^{- l3} • p² + 6,003 • 10 ^- 7 • p + 1'

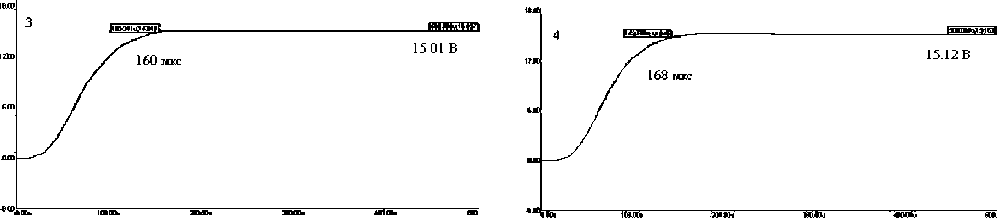
Этим вариантам соответствуют графики переходных процессов (рис. 3,4 и 5):

На основе анализа этих графиков сформулируем следующие выводы. Переходной процесс в системе четвертого порядка является оптимальным по быстродействию и имеет малое перерегулирование для третьего и четвертого вариантов (см. рис. 4). Наилучшим из них является третий вариант, который имеет меньшую статическую ошибку. В этом варианте отношение специальных коэф фициентов числителя и знаменателя равно 60. Следует отметить, что при крайних соотношениях специальных коэффициентов из интервала 30...150 параметры переходного процесса ухудшаются. Поэтому рекомендуется выбирать соотношение из интервала 50...70. Время регулирования, достигнутое в этом примере для стабилизатора напряжения с двухзвенным фильтром, равно 160 мкс.

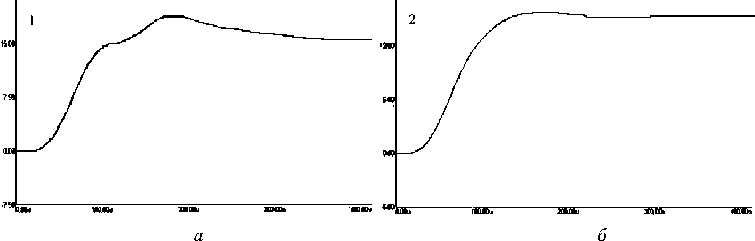
Рис. 3. Первый (а) и второй (б) варианты переходных процессов

б

Рис. 4. Третий (а) и четвертый (б) варианты переходных процессов

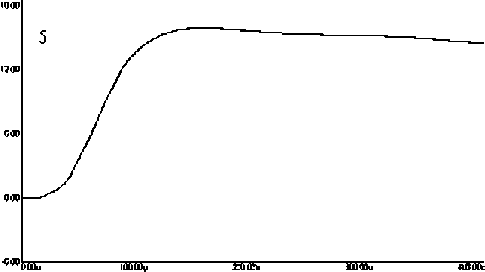
Рис. 5. Пятый вариант переходного процесса

Таким образом, предложенная в данной статье последовательность действий для формирования корректирующего звена системы четвертого порядка позволяет получить гарантированный результат при высоких показателях качества переходного процесса и простой практической реализации.