Определение параметров кровеносных сосудов по пульсовой волне

DOI:

Пульсовая волна представляет собой сложное совместное движение крови и стенок сосудов, описываемое нелинейной системой дифференциальных уравнений гидродинамики и теории упругости с подвижной границей. Даже приближенное решение такой задачи в настоящее время не представляется возможным без существенных упрощений, сводящих задачу к практически не интересным случаям. Поэтому для математического описания практически важных изменений пульсовой волны между нормой и патологией и выявления основных физических параметров, характеризующих патологию, необходимо построить феноменологическую модель, параметры которой определяются из сравнения с экспериментом.

Для скорости пульсовой волны воспользуемся известной эмпирической формулой [1–4]:

Eh

V =v Pd ■               (1)

где Е – модуль упругости, h – толщина, с – плотность стенки сосуда, d – диаметр кровеносного сосуда.

При наложении манжетки на область бицепса прохождение пульсовой волны, как и любой другой, через конечную по размерам неоднородность (длиной Lm) сопровождается возникновением отраженных волн от начала и конца манжетки. Датчик давления находится в середине манжетки, поэтому на него приходит прошедшая первую границу манжетки волна и волна, отраженная от второй границы манжетки. Следующие отражения не будем учитывать ввиду малости их амплитуды. Будем считать, что под манжеткой уменьшается диаметр сосудов. Тогда под манжеткой скорость волны увеличивается и от границ манжетки происходит отражение вследствие скачка акустического импеданса ρV. Кроме того, возникает топографическая неоднородность вследствие скачка диаметра сосудов под манжеткой, что также вызывает отражение, зависящее от отношения размера неоднородности и длины волны.

Импульс пульсовой волны Р ( t ) имеет спектр частот:

S p ⁽ f ) = ^I P ⁽ t ^{) cos ( 27ft} ) ^dt ,        (2)

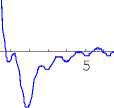
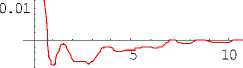
показанный на рисунке 2а для нормы, а на рисунке 2б при патологии.

Из рисунков 1б и 2б видно, что при патологии возникают высокочастотные осцилляции пульсовой волны. Для их описания можно предположить, что, по-видимому, при падении пульсовой волны на участок сосуда, пережатый манжеткой, возбуждаются колебания стенок сосуда. Поэтому предположим, что диаметр сосуда перед манжеткой d ₁, зависит от давления в виде:

d , ⁽ t ) = d ,0 { 1 + k , [ 1 + k vib ^{sin ( 2} n f vib t ^)] P ⁽ t ^)} ,      ⁽³⁾

а под манжеткой d ₂ и после манжетки d ₃ в виде:

d i ( t ) = d i0 ( 1 + k i P ( t )) ( i = 2,3 ) ,           (4)

где k ₁, k ₂, k ₃, k _vib, d ₁₀, d ₂₀, d ₃₀, f _vib – феноменологические параметры в соответствующих областях,

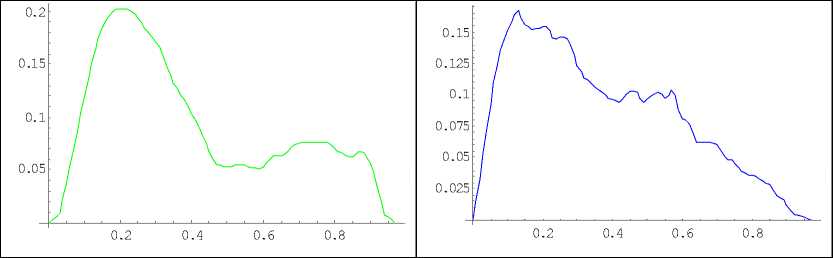
а) в норме                            б) при патологии

Рис. 1. Форма импульса пульсовой волны

ИННОВАЦИИ В БИОТЕХНОЛОГИЯХ

Р ( t ) – давление в пульсовой волне. Предположим также, что модуль упругости стенки сосуда зависит от диаметра и для разных областей сосуда имеет вид:

E i ( t ) = E о ( 1 + e d d i ( t )) ,                (5)

где E0, ed – феноменологические параметры. Толщина стенки сосуда также зависит от диаметра сосуда и задается очевидной формулой hi(t ) = h 0

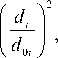
где h ₀ – феноменологический параметр. Зависимость от частоты f скорости распространения пульсовой волны в кровеносном сосуде возьмем в виде:

V ( f ) = V о ( 1 + Y 1 f + Y 2 f 2 ) ,           (7)

где V i₀ определяются формулой (1), y 1 , y ₂ - феноменологические параметры. Зависимость от частоты коэффициента отражения от границ манжетки (по аналогии с отражением акустических волн от границы раздела и топографической неоднородности), считая плотность сосуда р одинаковой во всех областях, примем в виде:

R ( f ) =

V i - V j

V i + V j

+ C

dv-dj f, i0

где V_i, V_j – скорости пульсовой волны, d_i, d_j – диаметры сосуда в разных областях, С ₁, – феноменологический параметр.

Полный интерференционный сигнал будем определять путем сложения (точнее, интегрирования) всех частотных составляющих пульсовой волны, прошедших первую границу манжетки и через интервал времени т/2=Lm/ 2V2 принятый в середине манжетки с учетом затухания частотных составляющих, пропорционального квадрату частоты

M ,(t ) = 272л да _____________ /     /      \ \

J V1 - R 1 ( f ) 2 S p ( f ) cos | 2п f 1 1 + I e - "“2” ^f 2/ V 2 ^L /2 df , ⁽⁹⁾

о                       V V ² J)

где R ₁( f ) – коэффициент отражения от первой границы манжетки, a - коэффициент затухания (феноменологический параметр), и частотных составляющих, отраженных от второй границы манжетки и принятых через интервал времени 3 т /2:

M 2 ( t ) = 272 л

J R 2 ( f )V 1 - R 1 ( f ) 2 S p ( f ) cos [ 2 n f [ t + 3 li e -“ 2 ” ^{f 2/} V2-^L m /2 df , ⁽¹⁰⁾ 0                              V ^{V 2 J})

где R ₂( f ) – коэффициент отражения от второй границы.

Таким образом, полный интерференционный сигнал, принятый датчиком в середине манжетки, определяется суммой

M(t) = M₁(t) + M₂(t) (11) и зависит от модельных параметров k_i , f _vib, e d , Y 1 , y ₂, С 1 , С 2 , “ , от материальных ( р i , Е 0 ) и геометрических ( d _i0, h ₀) параметров, являющихся феноменологическими и определяющими скорости и затухание пульсовой волны в различных частях сосуда в области манжетки.

Указанные 17 феноменологических параметров определяются методом наименьших квадратов при минимизации целевой функции

0.06

0.04

0.02

-0.02

0.06

0.05

0.04

0.03

0.02

• а)    в норме

• б)    при патологии

Рис. 2. Спектр пульсовой волны

F _c в виде суммы квадратов отклонений расчетной ( M ( t )) и экспериментальной ( P ( t )) характеристик:

N ²

F = £ ( M ( t ) - P ( t ))            (12)

k =1

На рисунке 3 представлены графики давления пульсовой волны в норме (зеленая кривая), при патологии сосудов (синяя кривая) и модельная кривая (красная), полученная при рассмотрении падения нормальной пульсовой волны на участок сосуда с манжеткой.

Целью расчета являлось определение параметров сосуда, при которых форма пульсовой волны становится близкой к патологической.

Представленная на рисунке 3 расчетная кривая соответствует следующим значениям параметров:

Е0= 26659 (Па/м2), ed = –14.3, d10= 6.7 мм, d20= 1.1 мм, d30= 4.8 мм, fvib = = 14.28 Гц, k1= 4.98, k2= 6.55, k3= 0.07, kvib = 0.08, h0 = 0.18 мм, p = 1150 (кг/м3),

C 1 = 48, С ₂ = -919, Y i = 0.047, y ₂ = 0.013, a = 0.0039.

Полученные результаты свидетельствуют о существенно нелинейном по давлению характере трансформации пульсовой волны в области манжетки. Обращает на себя внимание также обнаруженный эффект уменьшения модуля упругости при увеличении диаметра сосуда, о чем свидетельствует отрицательное значение коэффициента e_d .