Определение параметров модифицированного уравнения Эйринга для температурной зависимости вязкости жидкостей
Автор: Митыпов Ч.М., Дамдинов Б.Б., Ершов А.А.
Журнал: Вестник Бурятского государственного университета. Химия. Физика @vestnik-bsu-chemistry-physics
Статья в выпуске: 1, 2022 года.
Бесплатный доступ
С проблемами исследования вязкости приходится встречаться в технике, при разработке технологии разнообразных производственных процессов, при проектных работах и конструкторских расчётах, относящихся к самым различным жидким материалам. Изучением вязкости жидкостей занимаются сразу несколько направлений: физическая акустика, гидродинамика, молекулярно-кинетическая теория газов и жидкостей. В работе получена теоретическая зависимость вязкости жидкостей от температуры на основе модифицированного уравнения Эйринга. Проведена аппроксимация экспериментальных данных из справочных материалов. Показано, что большинство жидкостей разного типа подтверждают данную формулу. Проведен тщательный анализ полученных данных, обнаружена зависимость между силами межмолекулярного взаимодействия и вязким течением.
Вязкость жидкостей, строение жидкостей, уравнение эйринга, модификация, численное моделирование, структура, молярный и свободный объем, молекулы
Короткий адрес: https://sciup.org/148328070
IDR: 148328070 | УДК: 621.892 | DOI: 10.18101/2306-2363-2022-1-32-46
Текст научной статьи Определение параметров модифицированного уравнения Эйринга для температурной зависимости вязкости жидкостей
Митыпов Ч. М., Дамдинов Б. Б. Ершов А. А. Определение параметров модифицированного уравнения Эйринга для температурной зависимости вязкости жидкостей // Вестник Бурятского государственного университета. Химия. Физика. 2022. Вып. 1. С. 32–46.
Вязкость является одним из важнейших физических свойств вещества. Вязкость — способность вещества сопротивляться изменению структуры вещества, под действием механического воздействия. Силы трения, возникающие между слоями жидкости или газа при направленном движении слое относительно друг друга, называются силами вязкого трения.
Вязкость различных жидкостей и их смесей достаточно точно измерена для большинства веществ при различных температурах, но до сих пор не существует единой теории, объяснение её зависимости при различных температурах. В основном используются эмпирические формулы для описания вязкости жидких систем. Зависимость вязкости большинства жидкостей от температуры выражена формулой Френкеля [1]:
Eq
г] = В exp
RT
где B — эмпирический коэффициент, характеризующий вязкость при нулевой температуре, E 0 — энергия активации вязкого течения, который также определяется опытным путем.
Для определения физического смысла постоянных в теории вязкости жидкостей Эйринг [2] предположил, что процесс вязкого течения имеет определенную скорость. Используя теорию абсолютных скоростей реакций и химической кинетики Аррениуса, Эйринг получил следующую формулу:
N(2mnkTУ,2
П =
где ʋ f — «свободный» объем, E 0 — энергия активации (потенциального барьера). Он предполагал, что в процессе вязкого течения молекулы должны преодолевать энергетический барьер между двумя соседними положениями. Энергия этого барьера и есть энергия активации вязкого течения.
Несмотря на то, что молекулы жидкости упакованы довольно плотно, в этой же упаковке все же имеется свободное пространство, зависящее от структуры самого вещества. С макроскопической точки зрения, свободный объем одного моля вещества можно выразить через это выражение:
ʋ f = V — ʋ m N A
где V — молярный объем, ʋ m — объем молекулы, N A — постоянная Авогадро. Исходя из уравнения суммы состояний молекул в жидкости, и согласно термодинамическим выражениям, внешнее давление выражается следующим образом
[3]:
p = RT
дЕ dv
где Eʋap — энергия испарения на молекулу жидкости, ʋ — объем, занимаемый молекулой. Теперь необходимо вывести соотношение, связывающее свободный объем с величиной ʋ, который означает эффективный объем, занимаемый моле- кулой. Каждая молекула колеблется вокруг своего занимаемого места в определенной потенциальной «яме» из-за межмолекулярного взаимодействия, образуя вокруг себя некую виртуальную сферу, которая называется эффективным объемом. Следует отметить, что молекула имеет локализованный характер. Тогда объем жидкости можно представить в следующем виде:
V = ʋN A 5)
Здесь ʋ — эффективный объем молекулы. Следовательно, уравнение (2) преобразуется к следующему виду:
ʋ f = ʋN A -ʋ m N A = N A (ʋ -ʋ m ) (6)
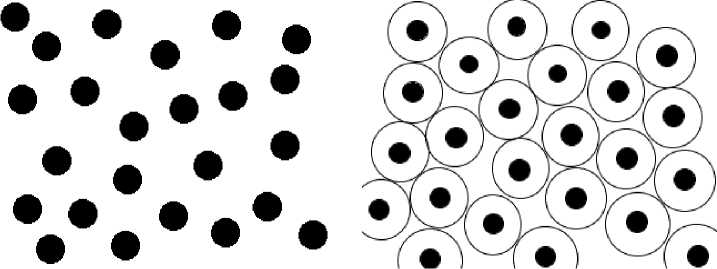
Рис. 1. Внутреннее строение жидкости
На рис. 1 изображено внутреннее строение жидкости: где черными точками обозначены молекулы, а сферы, нарисованные вокруг молекул, указывают на эффективный объем ʋ. Пустое пространство внутри сферы характеризует свободный объем ʋ f . Следует отметить, что каждая сфера имеет различный объем, но с учетом их большого количества, мы берем среднее значение. Также мы не учитываем свободное пространство, не входящее в сферы, и считаем их бесконечно малым. Сжатие и расширение жидкости происходит вследствие изменения
ʋ f .
Дифференцируя уравнение (3), подставив формулу для объема, получаем
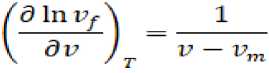
Согласно Эйрингу, производную от энергии испарения по объему прибли-
женно можно заменить на:
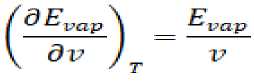
После подстановок и дифференцирования, конечный вид уравнения (3) вы-
глядит следующим образом:
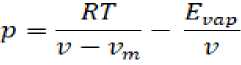
Внешнее давление мало по сравнению с E ʋap /ʋ , поэтому значением p можно вообще пренебречь, вследствие чего уравнение (8) примет следующий вид:
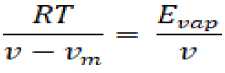
Если теперь ʋ — ʋ m заменить на ʋ f /N A и ʋ на V/V A , получаем
RTNa = EvapNA => = RTV
Vf V Vf Euap с помощью которой можно вычислить свободный объем жидкости.
Из-за того, что процесс вязкого течения связан с образованием свободного пространства, энергия активации вязкого течения должен составлять некоторую долю от теплоты испарения:
E .
■p v д p /1
^0 — (12)
n где n — коэффициент, показывающий, какая доля энергии испарения приходиться на вязкое течение. Тогда выражение для вязкости при подстановке выражений для свободного объема (10) и энергии активации будет выглядеть следующим образом:
N^nMkY^R^T5/6 (Euap\
^ = pr2/3 £ 175 exP y^RT / (13)
Сам же Эйринг, получил следующую формулу:
N2^Q2KMky/2RT3/2 /Evap\ n =---j^-----exP te) * ^vap xtwvi /
Как мы видим, уравнение Эйринга значительно отличается от выражения, в частности от предэкспоненциальным коэффициентом, полученного нами, хотя и присутствует аналогия. В уравнения (13) и в уравнении (14) температурная зависимость выражается T5/6 и T3/2 соответственно. Кроме того, отличаются с показа- тели степени для теплоты испарения и числа частиц.
Материалы и метод расчета
Объектами исследования являлись органические жидкости, низкотемпературные конденсированные газы, а также вода при различных температурах. Отметим, что плотность и теплота испарения зависит от температуры, поэтому были выбраны значения плотности при нормальных условиях и теплота испарения при температуре кипения.
При прямых расчетах формула (13) дает значения порядка 1013. С учетом этого, потребовалось ввести поправочный эмпирический коэффициент C .
cNUnMky/2RY/3T5/6 (EvaB\
П =----V^3Evapx^---- 6XP (15)
Таким образом, в модифицированном уравнении Эйринга, эмпирическими константами являются коэффициенты n и c. Для определения этих параметров был использован регрессионный анализ. В качестве метода оптимизации был выбран алгоритм Левенберга-Марквардта [4], который заключается в последовательном приближении заданных начальных параметров к исходным данным. Алгоритм в целом представляет собой аппроксимацию данных к заранее заданной произвольной функции. В качестве расчетной программы использовался мате- матический пакет Mathcad 15, так как в нем имеется встроенный алгоритм нелинейного регрессионного анализа.
Для начала находился молярный объем соответствующей жидкости, который зависит от температуры, что косвенно является функцией плотности. Для вычисления молярного объема были взяты значения плотности при нормальных условиях (или близких к нему), и считалось, что она постоянна.
V = M/ρ (16)
где ρ — плотность вещества (кг/м3).
Справочные данные плотности и энтальпий испарения были взяты из следующих различных источников [5-8]. Величина констант в уравнении (15):
R = 8,3144 Дж·моль-1·К-1, k = 1,38·10-23 Дж/К, N = 6,023·1023
Алгоритм Левенберга-Марквардта требует заранее заданных параметров (эмпирических коэффициентов) уравнения (хотя бы для одного параметра), к которым будет коррелироваться исходные данные. Эйринг рассчитал [2], что значение множителя n, который связан с размером вакансий, находится в интервале от 1 до 5. Поэтому в программе последовательно изменялось значение n от 1 до 5, одновременно рассматривая среднюю абсолютную погрешность. Следовательно, было выбрано то значение, при котором средняя абсолютная погрешность минимальна. Второй параметр, который является коэффициентом c, определялся произвольным образом самой программой на основе исходных данных.
Для достоверности результатов была вычисленасредняя ошибка аппроксимации соответствующих уравнений вязкости для каждого вещества:
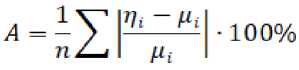
где ηi — вязкость, рассчитанная аппроксимацией уравнения (13), μi — значение экспериментальных данных вязкости.
Вывод и обсуждение результатов
В качестве объектов исследования были взяты температурные данные динамической вязкости жидких органических веществ в том числе, низкотемпературные конденсированные газы, а также несколько неорганических жидкостей. Полученные результаты были занесены в табл. 1.
Таблица 1 Результаты расчетов.
(результаты с (*) — вещества с явными водородными связями, с (**) — вещества с аномальным показателем n)
|
Вещество |
Форму -ла |
т , К |
p , кг/м3 |
F “vap , кДж/моль |
c |
n |
Л, % |
|
НЕОРГАНИЧЕСКИЕ ВЕЩЕСТВА |
|||||||
|
Вода* |
Н 2 O |
273-373 |
1000 |
40,6 |
6,45×10-23 |
2,16 |
4,67 |
|
Гидразин |
N 2 Н 4 |
278-298 |
1010 |
44,7 |
1,15×10-21 |
3,76 |
0,14 |
|
Бром |
Br 2 |
273-333 |
3102 |
30,8 |
1,42×10-21 |
3,19 |
0,15 |
|
Свинец |
Pb |
628-1128 |
11341 |
177,8 |
5,14×10-21 |
11,7 |
0,75 |
|
Олово |
Sn |
513-1073 |
7310 |
296,0 |
8,66×10-21 |
26,5 |
2,75 |
|
АЛКАНЫ |
|||||||
|
Этан |
С 2 Н 6 |
101-201 |
561 |
14,7 |
2,62×10-20 |
3,61 |
6,50 |
|
Пропан |
С 3 Н 8 |
81-175 |
500 |
19,4 |
6,26×10-21 |
4,08 |
15,64 |
|
н -Бутан |
С 4 Н 10 |
203-273 |
601 |
22,4 |
2,14×10-21 |
3,29 |
1,01 |
|
Изобутан |
С 4 Н 10 |
203-273 |
582 |
21,3 |
1,63×10-21 |
2,84 |
0,98 |
|
н -Пентан |
С 5 Н 12 |
153-303 |
626 |
25,8 |
1,97×10-21 |
3,37 |
3,44 |
|
н -Гептан |
С 7 Н 16 |
100,2 |
679 |
31,7 |
8,12×10-22 |
2,85 |
5,75 |
|
н -Нонан |
С 9 Н 20 |
263-423 |
718 |
37,2 |
1,22×10-21 |
3,11 |
0,23 |
|
н -Декан |
С 10 Н 22 |
243-293 |
730 |
40,0 |
6,52×10-22 |
2,84 |
1,18 |
|
н -Ундекан |
С 11 Н 24 |
263-473 |
740 |
40,1 |
8,74×10-22 |
2,84 |
1,89 |
|
н -Додекан |
С 12 Н 26 |
263-373 |
749 |
43,7 |
6,82×10-22 |
2,84 |
2,12 |
|
н -Тридекан |
С 13 Н 28 |
273-473 |
756 |
45,6 |
7,17×10-22 |
2,87 |
3,06 |
|
н -Тетрадекан |
С 14 Н 30 |
283-373 |
762 |
47,7 |
5,96×10-22 |
2,83 |
2,04 |
|
н -Пентадекан |
С 15 Н 32 |
293-373 |
768 |
49,4 |
6,31×10-22 |
2,87 |
1,68 |
|
н -Гексадекан |
С 16 Н 34 |
293-513 |
733 |
51,5 |
6,71×10-22 |
2,93 |
2,89 |
|
н -Гептадекан |
С 17 Н 36 |
303-573 |
777 |
53,1 |
7,26×10-22 |
2,98 |
2,87 |
|
н -Октадекан |
С 18 Н 38 |
303-373 |
776 |
54,8 |
5,60×10-22 |
2,90 |
0,95 |
|
н -Эйкозан |
С 20 Н 42 |
313-493 |
778 |
57,8 |
6,83×10-22 |
3,01 |
3,25 |
|
ЦИКЛОАЛКАНЫ |
|||||||
|
Циклопентан |
С 5 Н 10 |
273-313 |
751 |
27,3 |
1,32×10-21 |
2,74 |
0,24 |
|
Метилциклопентан |
С 6 Н 12 |
248-323 |
749 |
29,4 |
2,05×10-21 |
3,11 |
6,32 |
|
Этилциклопентан |
С 7 Н 14 |
253-323 |
763 |
31,9 |
1,77×10-21 |
3,16 |
0,38 |
|
Циклогексан** |
С 6 Н 12 |
283-353 |
774 |
29,9 |
5,57×10-22 |
2,11 |
0,38 |
|
Метилциклогексан** |
С 7 Н 14 |
273-313 |
770 |
31,2 |
1,00×10-21 |
2,58 |
0,07 |
|
Этилциклогексан |
С 8 Н 16 |
273-313 |
779 |
34,0 |
1,24×10-21 |
2,82 |
0,11 |
|
АЛКЕНЫ |
|||||||
|
Этилен |
С 2 Н 4 |
108-173 |
566 |
13,5 |
2,19×10-21 |
3,31 |
0,58 |
|
Пропилен** |
С 3 Н 6 |
88-174 |
609 |
18,4 |
1,66×10-23 |
2,36 |
21,95 |
|
Пентен-1 |
С 5 Н 10 |
183-273 |
635 |
25,2 |
3,20×10-21 |
3,79 |
6,11 |
|
Гексен-1 |
С 6 Н 12 |
218-313 |
673 |
28,6 |
1,65×10-21 |
3,35 |
1,49 |
|
Гептен-1 |
С 7 Н 14 |
273-368 |
697 |
31,5 |
1,71×10-21 |
3,42 |
0,72 |
|
Октен-1 |
С 8 Н 16 |
273-388 |
710 |
34,1 |
1,52×10-21 |
3,31 |
0,36 |
|
Циклогексен** |
С 6 Н 10 |
273-313 |
806 |
30,4 |
1,04×10-21 |
2,62 |
0,05 |
|
АЛКАДИЕНЫ |
|||||||
|
Бутадиен-1,3** |
С 4 Н 6 |
253-333 |
621 |
22,4 |
4,49×10-22 |
2,25 |
1,60 |
|
АРОМАТИЧЕСКИЕ УГЛЕВОДОРОДЫ (АРЕНЫ) |
|||||||
|
Толуол |
С 7 Н 8 |
273-453 |
862 |
33.2 |
1,08×10-21 |
2,95 |
2,24 |
|
о -Ксилол |
С 8 Н 10 |
268-393 |
875 |
36,2 |
1,08×10-21 |
2,99 |
0,49 |
|
м- Ксилол |
С 8 Н 10 |
273-453 |
864 |
35,6 |
1,98×10-21 |
3,57 |
4,02 |
|
п- Ксилол |
С 8 Н 10 |
283-403 |
861 |
35,6 |
1,21×10-21 |
3,15 |
0,58 |
|
Этилбензол |
С 8 Н 10 |
253-353 |
867 |
35,6 |
1,57×10-21 |
3,31 |
0,69 |
|
Изопропилбензол |
С 9 Н 12 |
273-313 |
857 |
38,0 |
1,11×10-21 |
3,14 |
0.22 |
|
н- Бутилбензол |
С 10 Н 14 |
283-353 |
795 |
38,8 |
1,15×10-21 |
3,03 |
0,49 |
|
Винилбензол |
С 8 Н 8 |
273-413 |
906 |
38,7 |
8,85×10-22 |
3,11 |
1,25 |
|
СПИРТЫ |
|||||||
|
Метанол* |
СН 4 O |
173-333 |
792 |
37,4 |
2,00×10-22 |
2,61 |
19,58 |
|
Этанол* |
С 2 Н 6 O |
175-348 |
789 |
38,5 |
3,40×10-22 |
2,64 |
3,99 |
|
Аллиловый спирт* |
С 3 Н 6 O |
273-363 |
854 |
40,0 |
1,99×10-22 |
2,30 |
1,11 |
|
Пропиловый спирт* |
С 3 Н 8 O |
213-373 |
800 |
41,4 |
1,89×10-22 |
2,19 |
4,82 |
|
Изопропанол* |
С 3 Н 8 O |
213-353 |
785 |
39,8 |
3,63×10-23 |
1,72 |
3,72 |
|
Бутиловый спирт* |
С 4 Н 10 O |
223-393 |
810 |
43,3 |
1,15×10-22 |
2,07 |
3,17 |
|
Изобутиловый спирт* |
С 4 Н 10 O |
233-373 |
801 |
41,8 |
1,64×10-23 |
1,59 |
3,53 |
|
Этиленгликоль* |
С 2 Н 6 O 2 |
293-413 |
1113 |
50,5 |
1,61×10-23 |
1,69 |
10,98 |
|
Глицерин* |
С 3 Н 8 O 3 |
273-473 |
1261 |
61,0 |
3,24×10-29 |
0,84 |
47,02 |
|
ОРГАНИЧЕСКИЕ КИСЛОТЫ |
|||||||
|
Муравьиная кислота* |
СН 2 O 2 |
283-373 |
1219 |
22,7 |
2,39×10-22 |
1.37 |
1,97 |
|
Уксусная кислота* |
С 2 Н 4 O 2 |
293-373 |
1082 |
23,7 |
7,14×10-22 |
1,79 |
0,33 |
|
Пропионовая кислота* |
С 3 Н 6 O 2 |
273-413 |
990 |
29,6 |
1,02×10-21 |
2,37 |
0,68 |
|
Масляная кислота** |
С 4 Н 8 O 2 |
273-433 |
956 |
41,0 |
7,85×10-21 |
2,85 |
0,74 |
|
Валерьяновая кислота** |
С 5 Н 10 O 2 |
288-363 |
940 |
44,1 |
6,78×10-21 |
2,80 |
2,10 |
|
ЭФИРЫ |
|||||||
|
Метилформиат |
С 2 Н 4 O 2 |
273-303 |
970 |
27,9 |
1,31×10-21 |
3,11 |
0,37 |
|
Этилформиат |
С 3 Н 6 O 2 |
273-343 |
917 |
29,9 |
1,26×10-21 |
3,09 |
0,73 |
|
Метилацетат |
С 3 Н 6 O 2 |
273-413 |
933 |
30,3 |
8,38×10-21 |
2,89 |
2,78 |
|
Этилацетат |
С 4 Н 8 O 2 |
273-343 |
902 |
31,9 |
7,75×10-21 |
2,83 |
4,17 |
|
Диэтиловый эфир |
С 4 Н 10 O |
74,12 |
714 |
26,5 |
9,52×10-22 |
2,93 |
7,25 |
|
Метилпропиловый эфир |
С 4 Н 10 O |
273-303 |
660 |
26,7 |
1,63×10-21 |
3,17 |
0,26 |
|
Пропилацетат |
С 5 Н 10 O 2 |
273-363 |
888 |
33,9 |
9,56×10-22 |
2,94 |
0,62 |
|
Этилпропионат |
С 5 Н 10 O 2 |
273-363 |
884 |
33,9 |
1,18×10-21 |
3,14 |
0,49 |
|
Метилизобутилов. эфир |
С 5 Н 12 O |
88,15 |
700 |
28,0 |
1,48×10-21 |
3,07 |
0,09 |
|
Этилпропиловый эфир |
С 5 Н 12 O |
273-323 |
750 |
28,9 |
1,37×10-21 |
3,11 |
0,23 |
|
Бутилацетат |
С 6 Н 12 O 2 |
273-373 |
881 |
36,3 |
9,25×10-22 |
2,95 |
0,30 |
|
Изобутилацетат |
С 6 Н 12 O 2 |
293-400 |
871 |
35,9 |
8,93×10-22 |
2,91 |
4,63 |
|
Этилбутаноат |
С 6 Н 12 O 2 |
288-343 |
879 |
35,5 |
1,15×10-22 |
3,08 |
0,73 |
|
Дипропиловый эфир |
С 6 Н 14 O |
273-343 |
736 |
31,3 |
1,28×10-21 |
3,04 |
0,30 |
|
Этилпентаноат |
С 7 Н 14 O 2 |
273-373 |
877 |
36,9 |
1,02×10-21 |
2,97 |
0,50 |
|
Дибутиловый эфир |
С 8 Н 18 O |
273-373 |
758 |
36,5 |
1,11×10-21 |
3,04 |
0,49 |
|
Бензилбензоат** |
С 14 Н 12 O 2 |
278-373 |
1120 |
53,6 |
2,31×10-23 |
1,91 |
13,49 |
|
Дибутилфталат** |
С 16 Н 22 O 4 |
288-308 |
1050 |
79,2 |
1,86×10-24 |
2,17 |
4,20 |
|
ГАЛОГЕНИДЫ УГЛЕВОДОРОДОВ |
|||||||
|
Тетрахлорметан** |
СCl 4 |
273-373 |
1590 |
29,8 |
7,52×10-22 |
2,39 |
0,41 |
|
Хлороформ |
СНCl 3 |
260-333 |
1483 |
29,2 |
1,35×10-22 |
3,01 |
0,72 |
|
Дихлорметан |
СН 2 Cl 4 |
253-313 |
1326 |
28,1 |
1,45×10-21 |
3,15 |
0,52 |
|
Иодметан |
СН 3 I |
273-313 |
2279 |
27,3 |
1,58×10-21 |
3,28 |
0,32 |
|
Тетрахлорэтилен |
С 2 Cl 4 |
273-393 |
1623 |
34,7 |
1,81×10-21 |
3,39 |
0,58 |
|
Трихлорэтилен |
С 2 НCl 3 |
263-348 |
1464 |
31,4 |
2,05×10-21 |
3,54 |
0,58 |
|
1,2-дихлорэтан** |
С 2 Н 4 Cl 2 |
273-353 |
1253 |
32,0 |
8,94×10-22 |
2,68 |
0,55 |
|
1,2-дибромэтан** |
С 2 Н 4 Br 2 |
273-393 |
2180 |
34,7 |
8,53×10-22 |
2,62 |
0,67 |
|
Хлорэтан |
С 2 Н 5 Cl |
253-313 |
903 |
24,6 |
1,50×10-21 |
3,06 |
0,59 |
|
Бромэтан |
С 2 Н 5 Br |
153-433 |
1455 |
27,0 |
1,55×10-21 |
3,19 |
10,11 |
|
Йодэтан |
С 2 Н 5 I |
273-343 |
1940 |
29,4 |
1,69×10-21 |
3,29 |
0,42 |
|
Аллилхлорид |
С 3 Н 5 Cl |
273-313 |
937 |
29,0 |
1,37×10-21 |
3,24 |
0,95 |
|
Аллилбромид |
С 3 Н 5 Br |
273-343 |
1398 |
30,2 |
1,52×10-21 |
3,26 |
0,31 |
|
1-хлорпропан |
С 3 Н 7 Cl |
273-318 |
890 |
27,2 |
1,31×10-21 |
2,94 |
0,17 |
|
2-хлорпропан |
С 3 Н 7 Cl |
273-303 |
862 |
26,3 |
9,86×10-22 |
2,71 |
0,52 |
|
1-бромпропан |
С 3 Н 7 Br |
273-313 |
1354 |
29,8 |
1,46×10-21 |
3,14 |
1,27 |
|
2-бромпропан |
С 3 Н 7 Br |
273-323 |
1310 |
28,3 |
1,22×10-21 |
2,89 |
1,48 |
|
1-йодпропан |
С 2 Н 5 I |
273-373 |
1747 |
32,1 |
1,52×10-21 |
3,19 |
0,60 |
|
2-йодпропан |
С 2 Н 5 I |
273-353 |
1703 |
30,7 |
1,43×10-21 |
3,06 |
0,48 |
|
Хлорбензол |
С 6 Н 5 Cl |
273-513 |
1107 |
35,2 |
1,40×10-21 |
3,17 |
0,73 |
|
Бромбензол |
С 6 Н 5 Br |
273-415 |
1495 |
37,8 |
1,48×10-21 |
3,29 |
1,03 |
|
Йодбензол |
С 6 Н 5 I |
283-413 |
1823 |
39,5 |
1,27×10-21 |
3,12 |
1,08 |
|
НЕКОТОРЫЕ УГЛЕВОДОРОДЫ |
|||||||
|
Пропаналь |
С 3 Н 6 O |
273-313 |
1070 |
28,3 |
2,04×10-21 |
3,51 |
2,41 |
|
Ацетофенон |
С 8 Н 8 O |
289-368 |
1028 |
44,0 |
1,10×10-21 |
3,13 |
3,42 |
|
Уксусный ангидрид |
С 4 Н 6 O 3 |
273-393 |
1082 |
38,2 |
1,01×10-24 |
3,12 |
0,65 |
|
Анилин* |
С 6 Н 7 N |
268-393 |
1022 |
42,4 |
7,45×10-24 |
1,49 |
19,66 |
|
Фенол* |
С 6 Н 6 O |
293-413 |
1070 |
45,7 |
3,61×10-24 |
1,41 |
16,02 |
|
Нафталин** |
С 10 Н 8 |
353-425 |
962 |
43,2 |
1,12×10-23 |
1,54 |
3,93 |
|
Ацетон |
С 3 Н 6 O |
183-323 |
790 |
29,1 |
1,33×10-21 |
3,20 |
1,57 |
|
Нитробензол |
С 6 Н 5 NO 2 |
273-480 |
1199 |
48,9 |
8,36×10-22 |
3,30 |
3,62 |
Уравнение (14) удовлетворительно описывает зависимость вязкости от температуры для большинства жидкостей, так как среднее значение относительной погрешности для 105 различных веществ, включая жидкие металлы, конденсированные неорганические газы, жидкие углеводороды составило
Лср.=2^^ = 3,16%, (18)
1=1
что говорит об истинности данной формулы, но требует более подробного разбора.
Также был произведен расчет доли свободного объема по следующей формуле:
k = ʋf/V·100% (19)
Анализ полученных результатов показал, что величина n зависит от теплоты испарения, a коэффициент с зависит от молекулярной массы и плотности. Теплота испарения является величиной, при котором молекулы становятся свободными, теряя все межмолекулярные связи.
Если в молекуле содержится гидроксильная группа в молекуле (фенолы, спирты, карбоновые кислоты), то атомы кислорода гидроксильных групп двух молекул могут тесно сблизиться, образуя водородную связь. В гидроксильной группе положительный конец диполя находится у атома водорода, благодаря чему через водород может образовываться связь с анионами или электроотрицательными атомами, имеющими неподеленные пары, например, с атомом кислорода другой молекулы. В общем, сила водородной связи зависит от электроотрицательности связанных атомов. Чем больше разность электроотрицательностей атомов, тем сильнее водородные связи. В жидком аммиаке и аминах водородные связи более прочные, чем в воде и спиртах [9].
Жидкости с водородными связями называются «ассоциированными» жидкостями. Величина n, характеризующая долю энергии активации от теплоты испарения, является максимальной энергией вязкого течения, если рассматривать вязкость как процесс перемещения молекул в веществе. Следовательно, в ассо- циированных жидкостях значение n должно быть гораздо меньше, чем в неассо-циированых жидкостях. Расчеты показали, что в жидкостях.
Propane
n-Nonane
Ph n i? •••
l
>
T , T
250 300 350 400 450
T , T
Temperature (K)
Temperature (K)
T , T
Ethylene
Temperature (K)
Butyric acid
Diethyl ether
T , T
T , T
Temperature (K)
Temperature (K)
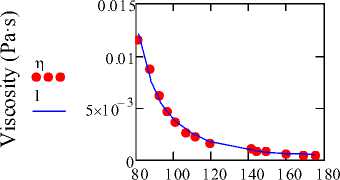
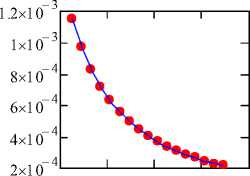
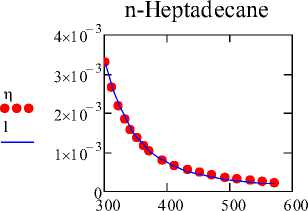
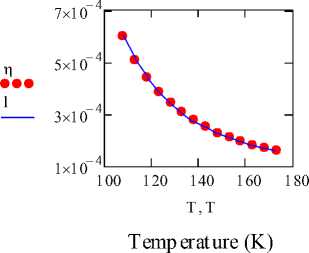
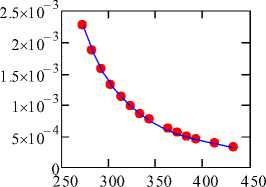
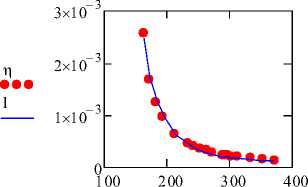
Рис. 2. Графики зависимостей вязкости различных веществ
(где точки означают значения экспериментальных данных, а линия означает вязкость, полученная модифицированным уравнением Эйринга)
Таблица 2
Погрешности результатов для некоторых веществ, полученные классическим уравнением Эйринга (столбец № 3) и модифицированным уравнением Эйринга (столбец № 4)
Таблица 3
Доля свободного объема при заданной температуре
|
Вещество |
, К |
к, % |
|
Вода |
273 |
5,59 |
|
Бром |
273 |
7,37 |
|
Пропан |
81 |
3,49 |
|
н -Пентан |
153 |
4,93 |
|
н -Тридекан |
273 |
4,99 |
|
Циклопентан |
273 |
8,31 |
|
Пентен-1 |
183 |
6,04 |
|
Октен-1 |
273 |
6,66 |
|
Бутадиен-1,3 |
253 |
9,36 |
|
Толуол |
273 |
6,84 |
|
о-Ксилол |
268 |
6,15 |
|
Винилбензол |
273 |
5,86 |
|
Метанол |
173 |
3,84 |
|
Изобутанол |
233 |
4,63 |
|
Уксусная кислота |
293 |
10,2 |
|
Масляная кислота |
273 |
5,53 |
|
Диэтиловый эфир |
163 |
5,11 |
|
Метилацетат |
273 |
7,49 |
|
Тетрахлометан |
273 |
7,61 |
|
1,2-дихлорэтан |
273 |
7,1 |
|
Бромэтан |
153 |
4,71 |
|
Хлорбензол |
273 |
6,45 |
|
Ацетон |
183 |
5,23 |
|
Нитробензол |
273 |
4,64 |
Оказалось, хотя это и очевидно, что пространственное строение молекул играет важную роль для образования межмолекулярных связей, а те в свою очередь влияют на макроскопические свойства вещества — вязкость, теплопроводность, теплоемкость и т.д. Было выяснено, что большинство органических соединений могут образовывать так называемые конформации — пространственные расположения молекул вращением вокруг одинарных связей (рис. 2). Конформации имеют определенную энергию.
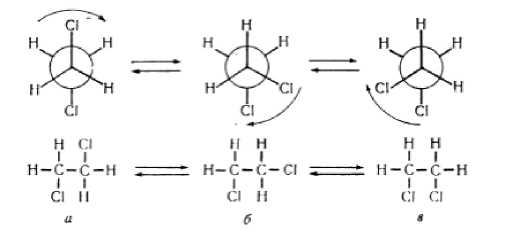
Рис. 3. Конформации 1,2-дихлорэтана. (Верхний ряд — вид вдоль связи С-С, нижний -структурная формула молекул; а — трансоидная (транс) конформация, б, в — скошенная (гош) конформация)
Для циклогексана возможны две энергетически возможные конформации молекул — аксиальные и экваториальные. При переходе их в друг друга аксиальные связи превращаются в экваториальные и наоборот. Такой процесс называют инверсией цикла. Инверсия осуществляется быстро, и циклогексан представляет смесь двух конформаций с одинаковой энергией. Частота перехода составляет 100000 раз в секунду, преодолевая большой энергетический барьер. Такое быстрое изменение конформаций создает флуктуации электронной плотности, которое влияет на межмолекулярные Ван дер Ваальсовы силы. Вероятнее всего процесс инверсии цикла в циклогексане и метилциклогексане повышает силу межмолекулярного взаимодействиях [10].
При применении уравнении вязкости (14) к эфирам показало, что при больших молекулярных массах, в частности, такие соединения как бензилбензоат и дибутилфталат, наблюдается низкий показатель значения n = 1,91 и n = 2,17 соответственно. Как мы ранее говорили, что низкий показатель величины n указывает на более сильную связь между молекулами. В спиртах и фенолах наличие сильной межмолекулярной связи объясняется наличием гидроксильной группы, из-за которой образуются водородные связи, тем самым повышая межмолекулярное взаимодействие. Структура бензилбензоата представляет соединение двух бензольных колец: один из бензойной кислоты, а другой бензольного спирта. Таким образом, можно было ожидать, что вращение бензольных колец может уменьшить межмолекулярные силы, но есть сведения, что большую силу межмолекулярной связи в бензилбензоате обеспечивают дисперсионные межмолекулярные силы, которые не зависит от строения и поля. Межмолекулярные силы, которые преобладают для бензилбензоата, являются силами дисперсии или Лондона. Они прямо пропорциональны молекулярной массе, и, сгруппировав несколько таких молекул, можно ожидать, что образование мгновенных и индуцированных диполей будет происходить с большей вероятностью [11]. А что касается дибутилфталата, расчеты показали низкое значение свободного объема — доля составляет всего 3 % от всего объема (у остальных веществ эта доля составила от 5 % и выше), что указывает на сильное межмолекулярное взаимодействие и требует дальнейшего изучения. Так как дибутилфталат неполярен, в нем вероятнее всего преобладают Лондоновские силы притяжения.
Среди галогенопроизводных углеводородов аномальное значение n обнаружено у тетрахлометана, 1,2–дибромэтана и дихлорэтана, а также 2-хлопропана, хотя они и не сильно выражены и находятся у верхней границы. Лондонские дисперсионные силы (LDF) присутствуют во всех молекулах, полярных или неполярных. Молекулы, также проявляющие диполь-дипольные взаимодействия (в дополнение к LDF), должны обладать более сильными силами притяжения, чем молекулы, которые проявляют только LDF. Но при сравнении с хлороформом, которое является полярной молекулой (дипольный момент D = 1,15 Дебая) межмолекулярное взаимодействие более слабое, чем в тетрахлометане. Это объясняется тем, что молекула хлора, находящаяся в тетрахлометане, обладает большим объемом по сравнению водородом. Поэтому тетрахлорметан имеет большую молекулярную поверхность, что увеличивает прочность межмолекулярных сил, и в этом случае перевешивает слабые диполь-дипольные взаимодействия, присутствующие в хлороформе. С помощью спектров комбинационного рассеяния све- та и спектров поглощения в инфракрасной области, а также путем измерения дипольных моментов и теплоемкостей было установлено, что 1,2 дихлорэтан представляет собой смесь трех конформаций (рис. 1) [12]. Рассмотрение трансоидной и скошенной форм 1,2-дибромэтана показывает, что эти конформации обладают различными дипольными моментами и имеет аналогичный характер как 1,2-дихлорэтана.
Следующее соединение, показывающее аномальные свойства, является нафталин. Он относится к полициклическим ароматическим углеводородам, имеющим два бензольных ядра наряду с азуреном. Все молекулы неполярны, поэтому вклада индукционных и ориентационных сил в межмолекулярное взаимодействие нет, но с другой стороны молекулы нафталина имеет плоскостное строение и большую молекулярную поверхность, что усиливает прочность дисперсионных сил Лондона (LDF). Подробный анализ структуры различных жидкостей и растворов можно найти в работах [13-15].
Заключение
Таким образом, модифицированное уравнение Эйринга показало высокую достоверность для большинства веществ в различных интервалах температур. Данная зависимость может быть использована для расчета коэффициентов динамической вязкости жидких веществ в широком диапазоне температур. Исключение составляет некоторые вещества, с высоким дисперсионным межмолекулярным взаимодействием (бензилбензоат, дибутилфталат), жидкости с конформационным инверсией цикла (циклогекса, 1,2–дихлорэтан и т.д.) В следующих работах будет рассмотрено значение второй эмпирической константы, определен физический смысл этого параметра.
Список литературы Определение параметров модифицированного уравнения Эйринга для температурной зависимости вязкости жидкостей
- Френкель Я. И. Кинетическая теория жидкостей Ленинград: Наука. ЛО, 1975. 594 с. Текст: непосредственный.
- Глесстон С., Лейдлер К., Эйринг Г. Теория абсолютных скоростей реакций. Москва: Издатинлит, 1948. 583 с. Текст: непосредственный.
- Глесстон С. Теоретическая химия. Москва: ИИЛ. 1950. 632 с. Текст: непосредственный.
- Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. Москва: Мир, 1985. 354 с. Текст: непосредственный.
- Варгафтик М. Б. Справочник по теплофизическим свойствам газов и жидкостей. Москва: Наука, 1972. 720 с. Текст: непосредственный.
- Справочник химика. Том 1. Общие сведения, строение вещества, свойства важнейших веществ, лабораторная техника I под ред. Б. П. Никольского. Москва; Ленинград: Химия, 1966. 1071 с. Текст: непосредственный.
- CRC Handbook of Chemistry and Physics. 84st Edition Edited by David R. Lide (National Institute of Standards and Technology). CRC Press: Boca Raton, FL. 2004. 2556 р.
- Грехов Л. В., Марков В. А. Эфиры — перспективные альтернативные моторные топлива для дизельных двигателей // Транспорт на альтернативном топливе. 2010. Т. 15, № 3. С. 62-71. Текст: непосредственный.
- Реутов О. А., Курц А. Л., Бутин К. П. Органическая химия: учебник: в 4 частях. Москва: Лаборатория знаний, 2020: Ч. 1. 8-е изд. 568 с.; Ч. 2. 9-е изд. 624 с.; Ч. 3. 7-е изд. 544 с.; Ч. 4. 6-е изд. 726 с. Текст: непосредственный.
- Илиел Э. Основы стереохимии. Москва: БИНОМ. Лаборатория знаний, 2009. 2-е изд. 119 с. Текст: непосредственный.
- National Center for Biotechnology Information. PubChem Compound Summary for CID 2345, Benzyl benzoate. Retrieved April 27, 2021 from https://pubchem.ncbi.nlm.nih.gov/ compound/Benzyl-benzoate.
- Матье Ж., Алле А. Принципы органического синтеза (Введение в изучение механизма органических реакций). Москва: ИЛ, 1962. 624 с. Текст: непосредственный.
- Headen T. F. Cullen P. L. Patel R., Taylor A., Skipper N. T. The structures of liquid pyridine and naphthalene: the effects of heteroatoms and core size on aromatic interactions // Phys. Chem. Chem. Phys. 2018. V. 20, № 4. P. 2704-2715.
- Damdinov B. B., Danilova V. A., Minakov A. V., Pryazhnikov M. I. Rheological Properties of PVDF Solutions // J. Sib. Fed. Univ. Math. Phys. 2021. 14(3). Р. 265-272.
- Badmaev B. B., Damdinov B. B. Investigation of shear elasticity of organic liquids by acoustical method // Acoustical Physics. 2001. V. 47, № 5. P. 561-563.


