Определение параметров положительной обратной связи адаптивной фрикционной муфты

Состояние вопроса. Идея применения в адаптивных фрикционных муфтах (АФМ) комбинированной положительно-отрицательной обратной связи выдвинута и обоснована в работах [1‒4]. Преимуществом комбинированной обратной связи, функционирующей в режиме разделения времени работы видов обратной связи, является повышение номинальной нагрузочной способности АФМ при небольших значениях коэффициента трения, меньших, чем f ( f ‒ среднее (расчетное) значение коэффициента трения), и, как следствие, повышение точности срабатывания муфт.

В качестве дискриминатора сигналов обратной связи применена фрикционная пара [5] или упругие элементы управляющего устройства (УУ) [6], изменение пространственного положения которых приводит при определенной величине коэффициента трения к изменению знака выходного сигнала УУ.

Постановка задачи исследования. Синтез положительноотрицательной обратной связи, действующей в составе АФМ в режиме разделения времени.

Решение задачи. Рассмотрим принципиальную схему АФМ, показанную на рис. 1, а. Передача вращающего момента между полумуфтами 1 и 2 осуществляется пакетом фрикционных дисков 3 и 4. Диски 3 соединены с нажимным диском 5, установленным на ступице полумуфты 1 с возможностью свободного поворота относительно      нее.

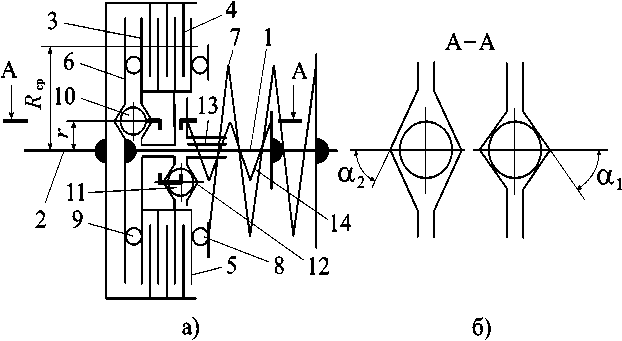
Рис. 1. Принципиальная схема АФМ с комбинированной обратной связью

Диски 4 соединены с барабаном полумуфты 2.

Силовое замыкание      пакета дисков 3 и 4 на упорный диск 6, жестко закрепленный на ступице полумуфты 1, осуществляет пружина 7 через упорные подшипники 8 и 9.

В муфте имеется два УУ. УУ отрицательной обратной связи состоит из тел качения 10, размещенных с зазором в скошенных гнездах, выполненных на торцах нажимного диска 5 и упорного диска 6 (рис. 1, б).

УУ положительной обратной связи состоит из тел качения 11, размещенных без зазора в скошенных гнездах, которые выполнены на торцах нажимного диска 5 и опорной втулки 12 (рис. 1, б). Опорный диск 12 смонтирован на ступице полумуфты 1 и соединен с нею направляющей шпонкой 13. Поджатие опорной втулки 12 в направлении нажимного диска 5 осуществляется пружиной 14.

Реализация комбинированной обратной связи в АФМ осуществляется на основе следующего принципа. Первоначальное натяжение пружины 14 выбирается таким, чтобы действующая на опорную втулку 12 распорная сила, возникающая на телах качения 11 при передаче вращающего момента, при значении f (где f ‒ минимальный коэффициент трения) превышала силу натяжения пружины 14, но не приводила к устранению зазора между телами качения 10 и соответствующими гнездами, в которых они размещены. При этом условии в муфте будет действовать только положительная обратная связь, что увеличивает момент сил трения фрикционной группы [7].

Отрицательная обратная связь в АФМ включается при значении коэффициента трения, большем, чем f , по следующей причине. Действие отрицательной обратной связи при минимальном коэффициенте трения привело бы к снижению величины момента сил трения и, как следствие, ‒ к уменьшению точности срабатывания АФМ [8].

Для математической модели АФМ, отражающей зависимость вращающего момента муфты от коэффициента трения, найдем указанные зависимости при действии только положительной обратной связи и при совместном действии отрицательной и положительной обратной связи. Зависимость для определения вращающего момента при действии положительной обратной связи:

T , = zR cp f ( F ni + F pi ),                            (1)

где z ‒ число пар трения фрикционной группы; R _ср ‒ средний радиус поверхностей трения дисков 3 и 4; f ‒ коэффициент трения; F п1 ‒ сила натяжения пружины 7; F _р1 ‒ распорная сила УУ положительной обратной связи, возникающая при взаимодействии тел качения 11 с боковыми стенками гнезд дисков 5 и 12 в процессе передачи вращающего момента.

Распорная сила F _р1 определяется по следующей формуле:

T

F = — tg ^a i ,                          (2)

r где r - радиус окружности, на которой расположены тела качения 11; а -угол скоса боковых стенок гнезд под тела качения 11 (рис. 1, б).

После подстановки соотношения (2) в формулу (1) получим уравнение первой степени относительно неизвестного T ₁, решение которого имеет вид:

^T1 = ZF ni^R ср f ^.                    (3)

1 ^{- zC}1 f

В решении (3) параметр   C 1   ‒ коэффициент усиления (КУ)

положительной обратной связи, вычисляемый по соотношению:

C 1 = ^{R сp} tg a , . r

Вопрос о величине распорной силы F р1 должен решаться на основе условия достижения ее максимального значения при минимальном коэффициенте трения. Выполнение указанного условия основано на дополнительном сжатии пружины 14 при воздействии тел качения 11 на опорный диск 12. Поворот нажимного диска 5 на соответствующий угол не должен приводить к устранению окружного зазора между телами качения 10 и соответствующими им боковыми стенками гнезд УУ.

В соответствии с этим запишем:

F p1 = F n2 +A F n2 + F тp ,                         (4)

где F _п2 ‒ начальная сила натяжения пружины 14; Δ F _п2 ‒ сила дополнительного сжатия пружины 14 в результате осевого перемещения вправо (рис. 1, а) опорного диска 12; F _тр ‒ сила трения между опорным диском 12 и направляющей шпонкой 13.

Поскольку рассматривается начальный период времени движения опорного диска 12, справедливо неравенство:

F pi >  F + F tp .                              (5)

В неравенстве (5) члены F _я и F соответственно равны:

z ⁽ F il ⁺ F 2 ) ^R cp ^f

^F pl =------------ — tg « i = zC i^f min ⁽ F + F i2 ) ,

r

„ _ 2 z ( F _nl + F _n 2 ) R _C p f _nin

Ftp                j            f 1 , где f1 ‒ коэффициент трения между опорным диском 12 и направляющей шпонкой 13 (принято f1=const); d ‒ диаметр посадочной поверхности ступицы полумуфты 1 под опорный диск 12.

Подставляя последние соотношения в неравенство (5), получаем:

F _n 2 + 2 z ( F _n i + F _n 2 ) R_C p f min f l / d        F_n2       ^2 R _C p f l

C >                                  =------- ¹²-- +         .      (6)

¹           Zfm.( F il + F _n 2 )           Zf min ( F^ + F _n 2 )      d

Неравенство (6) устанавливает минимальное значение КУ положительной обратной связи, при котором выполняется условие достижения максимального значения распорной силы Fр1.

Максимальное значение распорной силы F р1 при значении f min можно найти по соотношению (4), учитывая необходимость сохранения определенного зазора между телами качения 10 и боковыми стенками гнезд. На основе этого определяется конкретное значение C 1 .

Для последующего периода движения опорной втулки 12 при определении распорной силы F р1 необходимо использовать соотношение (3). С учетом этого находим:

T f

р1 - - t^g a 1 - z п^ 1 - zC^ f min .

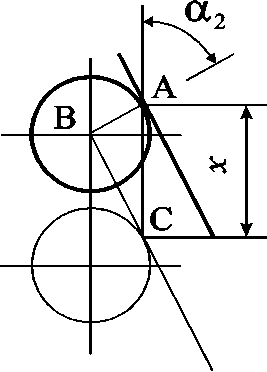
Рис. 2. Расчетная схема 1

Сила трения в шпоночном соединении вычисляется по формуле:

2 T 1 f 1с                     f min f 1с

тр" d ’    nl ср d(1 - zC1 f min)’ где f1c ‒ коэффициент трения скольжения в шпоночном соединении.

Для определения величины прироста силы ΔFп2 в формуле (4) обратимся к рис. 2, на котором показана схема перемещения тела качения 10 в гнезде УУ отрицательной обратной связи. Решая прямоугольный треугольник АВС, найдем длину пути, который проходит точка С, расположенная на поверхности тела качения, до момента его контакта со стенкой гнезда:

AC= x -

r

ш

, cos a2

где r _ш ‒ радиус тела качения 10; α₂ ‒ угол скоса гнезда под тело качения 10.

Если тела качения 10 и 11 равноудалены от оси вращения муфты, то перемещение точки контакта A тела качения 11 в окружном направлении также будет равно x (рис. 3). Соответствующее осевое перемещение опорной втулки 12 может быть найдено из прямоугольного треугольника АОС (рис. 3):

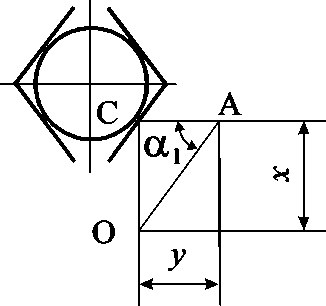
Рис. 3. Расчетная схема 2

AC - y -

x tgai ,

или, с учетом формулы (9):

y =

r ш

Iga, cos a2

Соответственно перемещению y сила дополнительного сжатия пружины 14 равна:

^2 =

cnrш tga cos a2

где n ‒ поправочный коэффициент, учитывающий необходимое фактическое перемещение опорной втулки 12 при значении f _min; c ‒ осевая жесткость пружины 14.

Поскольку прирост вращающего момента АФМ при действии только положительной обратной связи в интервале значений коэффициента трения f min … f к ( f к – граничное значение коэффициента трения, разделяющее режимы работы положительной и отрицательной обратной связи) не должен быть большим, значение коэффициента n принимают равным 0,7…0,9.

Учитывая соотношения (7), (8) и (10) в равенстве (4), найдем значение КУ положительной обратной связи:

_{c =} ² z ^Fn1^R ср f min fx с + d [ F n2 + ^СПГш ^/(t g ^a i ^{COS a} 2 ^{)] 1}        z ^df min^{[ F} n1 + ^F n2 + ^СПГш ^/( tg ^a i ^{C0S a} 2 ^)]

.

Значение коэффициента трения f _к, при котором начинает действовать отрицательная обратная связь, определяется на основе следующих рассуждений. Для повышения точности срабатывания АФМ вращающий момент при значении f _к не должна быть меньше вращающего момента при значении f _min. Выполнение данного условия является весьма важным, так как после начала действия отрицательной обратной связи резко уменьшается вращающий момент АФМ. Данный процесс отражен участком ВС на графике нагрузочной характеристики муфты T(f) , приведенном на рис. 4. На графике участок АВ соответствует действию в муфте только положительной обратной связи, а участок CD ‒ действию комбинированной связи.

Поскольку при значении коэффициента трения fк начинает действовать отрицательная обратная связь, формула для определения величины соответствующего вращающего момента принимает вид:

T = zR ср f к ( F^ + F р1 - F р2 ),

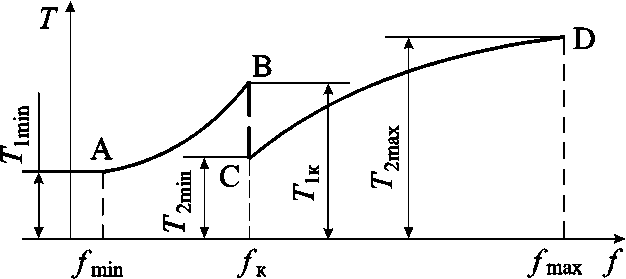
Рис. 4. Графики изменения величины вращающего момента АФМ в процессе автоматического регулирования

где Fя - распорная сила при          действии комбинированной обратной связи; Fр2 -распорная сила при действии отрицательной обратной связи.

Результаты исследования могут быть использованы при расчете и проектировании АФМ с комбинированной обратной связью при назначении параметров УУ положительной обратной связи.

Вывод. Разделение силового замыкания фрикционной группы и УУ положительной обратной связи АФМ повышает точность срабатывания не только за счет увеличения числа пар трения, но и за счет увеличения усилия замыкания фрикционной группы и уменьшения усилия замыкания УУ положительной обратной связи.