Определение параметров профиля трапецеидальной дифракционной решетки на основе полиномиальных аппроксимаций отраженного поля

При изготовлении микро- и наноструктур актуальной является проблема измерения и контроля их геометрических параметров. В последние годы возрос интерес к методам оптической рефлекто-метрии [1–8], поскольку они позволяют б ыстро бесконтактным неразрушающим способом измерять параметры микро- и наноструктур. С ущно сть метода рефлектометрии заключается в определении параметров исслед уемой структуры по измерениям характеристик отраженного поля при различны х параметрах сканирующего излучения (длина волны, поляризация, угол падения излучения). В работах [5–7] было показано, что точность определения геометрических параметров структур может прев ышать величину 1 нм.

Решение обратной задачи рефлектометрии состоит в определении геометрических параметров профиля решетки, обеспечивающих совпадение расчетных и измеренных значений параметров нулевого отраженного порядка дифракции. При этом прямая задача, состоящая в расчете отраженного поля при известных параметрах структуры, решается в рамках строгой электромагнитной теории.

В данной статье рассматривается решение обрат ной задачи оценки параметров диф ракционной решетки с трапецеидальным профилем. В предыдущей работе [8] авторами были представлены два метода реш ения аналогичной задачи. Метод 1 в [8] был основ ан на предварительном поиске параметров структуры по таблице характеристик отраженного поля с последующим использованием процедур оптимизации для уточнения параметров струк -туры. Метод 2 основывался на использовании нейронной сети. Предложенные в [8] методы обладаю т как достоинствами, так и недостатками. Так, метод 1 поиска по таблице с последующей оптимиза- цией позво ляет определять параметры трапецеидального профиля с высокой точностью (порядка 10–3 нм для линейных параметров, и 10–4 град уса – для угловых), но облад ает относительно невысокой скоростью работы (несколько секунд на одно измерение). Метод 2, использую щий нейронную сеть, облад ает несколько меньшей точностью (порядка 10–2 нм для линейных параметров, и 10–3 градуса – для угловых), но имеет сущ еств енно более высокую скорость работы (несколько десятков измерений в секунд у). Также к недостаткам метода 2 след ует отнести факт отсутствия четких критериев для выбора архитектуры сети, по которым мо жно было бы заранее опред елить точность решения обрат ной задачи .

В данной работе предложено два новых метода определения параметров дифракционных решеток с трапецеидальным профилем. Аналогично методу 1 в [8], методы основаны на предварительном поиске по таблице с послед ующей оптимизацией. В отличие от метода 1, для расчета сигнатур в процессе оптимизации используются полиномиальные интерполяции разного вида. Эффективность предложенных методов оценивается на примере определения параметров трапецеидального профиля. Приведенные результаты численных экспериментов показывают высокую точность и скорость предложенных методов.

Постановка задачи

Профиль симметричной дифракционной решетки с клином травления можно представить в виде равнобедренной трапеции (рис.1). Такой профиль однозначно описывается тремя параметрами: высотой решётки ( h ), длиной нижнего основания ( p ) и углом наклона боковых сторон ( α ) . Период решетки ( d ) и показатели преломления материалов решетки и подложки остаются неизменными .

Рис. 1. Профиль решётки с трапецеидальным профилем

Представим набор оцениваемых параметров профиля трапецеидальной решетки в виде вектора g = (h,p,а). Задача рефлектометрии состоит в определении g по измерениям параметров нулевого отраженного порядка дифракции при различных параметрах падающего пучка света vi = (Ai,Qi,ф-), i = 1,..., M , где Ai - длина волны, 9i - угол падения, фi - угол поляризации, M - число измерений. В нулевом отраженном порядке формируется эллиптически поляризованный пучок, у которого измеряются интенсивность отраженного порядка IR или параметры эллипса поляризации [9,10]. Эллипс поляризации описывается действительными параметрами tan Т и cos А , определяемыми из уравнения tanТexp(iА) = RE/RH , (1)

где RE , RH – комплексные коэффициенты для волн E- и H-типа, образующих эллиптически поляризованный пучок [3,7]. В качестве параметров поляризации также используются величины tan Т-1 „ „ г 2

а = \ „ w 1, в = cosА1 - а . (2) V tan Т +1

Методы определения параметров профиля решетки

Для простоты изложения б удем полагать, что измеряемой характеристикой отраженного светового пучка является интенсивность нулевого порядка I^R . Оценка параметров профиля основана на минимизации ф ункции ошибки

5 ( g ) = | |^S( g ) ^- S oil ^ min, ⁽³⁾ представляющей разность межд у расчетными S ( g ) = ( I R ( g ; V 1 ), ^ , I R ( g ; v m )) и измеренными значениями интенсивностей S 0 = ( I R ( v , ), ^ , I R ( v _M )). Векторы S ( g ) и S ₀ называют сигнатурами. Расчетные значения интенсивностей I^R ( g ; v _i ) в S ( g ) являются функциями от определяемых п араметров g , значения v _i рассматриваются как п араметры. Расчет S ( g ) (решение прямой задачи) основан на строгом решении задачи дифракции по методу Фурье-мод [14–17].

Для решения задачи оптимизации (3) предложено два метода. Первый метод основан на построении полиномиальных аппроксимаций для интенсивностей нулевого отраженного порядка

1R (g;v m )= 2 a4i2 ч (v m) hV 2“'3 , (4) i1 i2 -3,2 ij& Km где Km – степень полинома. Как правило, диапазоны изменения параметров h, p и а известны заранее (определяются технологией) и составляют несколько десятков нанометров. При этом использование полиномиальных аппроксимаций можно рассматривать как вариант теории возмущений . Для расчет а коэффициентов полинома aii i (vm ) выбирается некоторое обучающее множество T = {gi, i = 1,^, L} «характерных» параметров решетки. По обучающему множеств у параметров вычисляются интенсивности нулевого отраженного порядка. Далее, коэффициенты в (4) вычисляются по метод у наименьших квадратов из условия минимума квадрата разности между IR (g; vm) и IR (g; vm) при g e T. Выбор обучающего множества зависит от исслед уемой структуры. Представления (4) позволяют эффективно решать задачу оптимизации (3). Основная вычислительная нагрузка при этом приходится на предварительный этап построения полиномов (4). Вычисление S(g) в (3) вместо строгого решения задач дифракции сводится к вычислению полиномов. Представления (4) также позволяют аналитически вычислить производные функц ии ошибки (3).

Второй метод основан на построении таблицы сигнатур S ( g ) и послед ующей сплайновой интерполяции межд у узлами таблицы. Построение таблицы сигнатур происходит след ующим образом. Область допустимы х значений параметров покрывается равномерной сеткой с определенным по каждому параметру шагом А i ( i = h , p , а ). В каждом узле сетки, определяемом набором индексов k = ( k h , k p , к _а ), рассчитывается соответствующая сигнатура S ( g_k ) . Таким образом, формируется «таблица» параметров структуры и соответствующих им сигнатур. Далее по этой таблице строится N-размерный сплайн S ( g ) . Сплайн S ( g ) используется при решении задачи оптимизации (3). При этом вместо вычисления сигнатур S ( g ) , треб ующих решения задачи дифракции, используются значения интерполяционного сплайна S ( g ) .

Численные результаты

Приведем результаты работы двух предложенных методов для кремниевой решетки с симметричным трапецеидальным профилем (рис.1). Будем считать, что период решетки d =140нм, а измеряемы е параметры находятся в следующих диапазонах: h e [310,340]нм , p е [86,106]нм , ае [1,5] ° .

Расчет сигнатур проводился при след ующих параметрах падающего пучка: поляризация падающей волны – постоянная, ТМ (Е-волна), угол падения – постоянный, 71°, длина волны – переменная, от 300

до 900 нм. Число длин волн при расчете сигнатур в первом методе равно 50, во втором – 20. Указанные выборки из спектра падающего пучка являются достаточными для решения задачи оценки параметров с высокой точностью (лучше 0,1 нм).

Для оценки рабочих характеристик методов использовалась следующая схема численного эксперимента. В указанных выше диапазонах параметров ( h , p , а ) случайно генерируется тройка параметров g , для которой вычисляется вектор интенсивностей отраженного сигнала S 0 ( g ) . Сигнатура S 0 ( g ) рассматривается как измеренный сигнал. По S 0 ( g ) предложенными методами находятся оценки параметров g ɶ , которые сравниваются с исходными параметрами g . По результатам сравнения оценивается точность определения параметров ( A h , A p , Д а ) = g - g .

Для оценки параметров первым методом были построены аппроксимации для интенсивностей нулевого отраженного порядка в виде полиномов 6-ой степени

R m ( g ; A m ) = E « 12 - 3 ( A m ) ^' P ^ ^. (5) - 1 - 2 i 3 , E 0'^ 6

Обучающее множество T для построения полиномиальных аппроксимаций (5) формировалось из 2000 сигнатур, соответствующих множеств у троек параметров ( h , p , а ), сгенерированных случайным образом в заданном выше диапазоне. Время построения аппроксимаций (5) на стандартном персональном компьютере составляет 3-4 часа.

Рис. 2а-в демонстрируют результаты работы первого метода для 200 случайно сгенерированных троек параметров ( h , p , а ). Оценка параметров осуществлялась на основе минимизации н евязки (3) с использованием метода Лев енберга-Марквардта [11,12]. При этом для вычисления S ( g ) в (3) использовались полиномиальные аппроксимации (5).

Рис. 2а-в показывают, что первый метод позволяет определять параметры трапецеидального профиля с высокой точностью, превышающей 0,1 нм. Время решения задачи составляет десятые доли секунды.

Для оценки параметров по второму методу была построена таблица сигнатур с шагами дискретизации 1 нм по параметрам h и p и 0,4 ° по параметру а . По таблице был построен интерполяционный сплайн. Время расчета таблицы и построения аппроксимирующего табличные данные сплайна на стандартном персональном компьютере составляет 2-3 часа.

Рис.3а-в демонстрируют результаты работы второго метода для 200 случайно сгенерированных троек параметров ( h , p , а ). Оценка параметров осуществлялась на основе минимизации невязки (3) с использованием метода Левенберга-Марквардта [11,12]. При этом для вычисления S ( g ) в (3) использовалась сплайновая аппроксимация таблицы сигнатур.

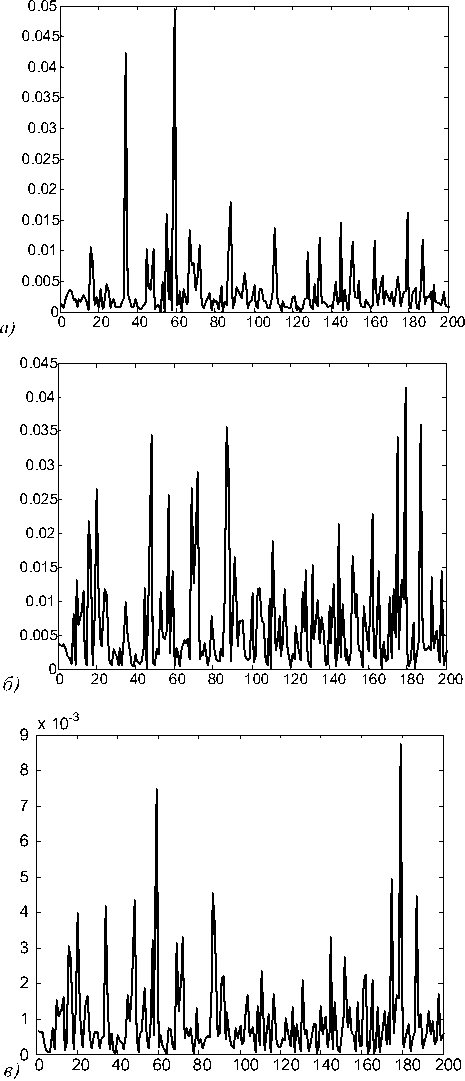
Рис. 2. Абсолютные отклонения сгенерированных параметров от найденных оценок при 200 испытаниях для первого метода: (а), (б) - | A h I и I A p I (в нанометрах), (в) - I Д а | (в градусах)

Рис.3а-в показывают, что второй метод также позволяет определять параметры трапецеидального профиля с высокой точностью, превышающей 0,1 нм. Время решения задачи также составляет десятые доли секунды.

Методы были использованы для оценки параметров профиля дифракционных структур по результатам реальных измерений.

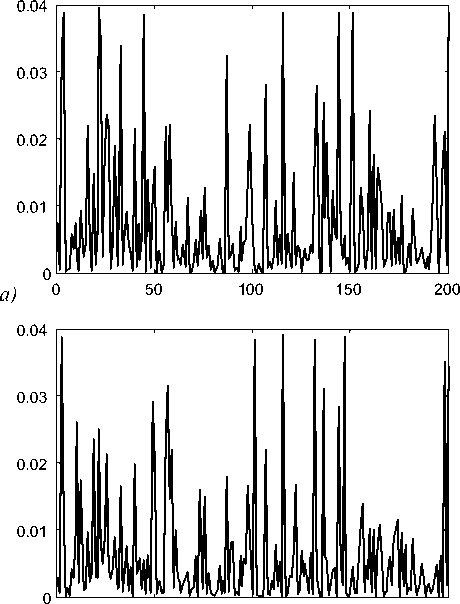
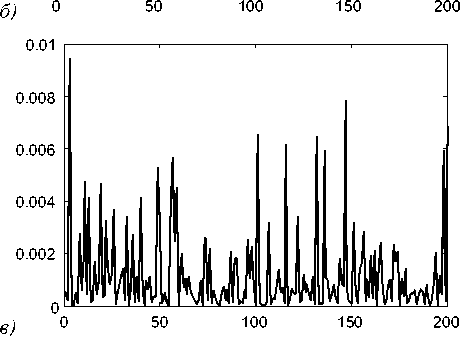
Рис. 3. Абсолютные отклонения сгенерированных параметров от найденных оценок при 200 испытаниях для второго метода: (a), (б) – | ∆ h | и ∆ p (в нанометрах), (в) – | ∆ α | (в градусах)

На рис.4 точ ечными линиями показаны измеренные сп ектры α(λ) и β(λ) (2) д иф ракцио нно й решетки из кремния с периодом d=140 нм, выполненные на эллипсометре UV1280SE компании TLA TENCOR. Предполагалось , что профиль решетки имеет трапецеидальную форму (рис.1). Для оценки параметров проф иля были использованы оба рассмотренных метода. Методы выд али фак-тич ески совпад ающие оценки параметров : h=321,6 нм, p=98,16 нм, α=2,9°. Рассчитанные спектры α(λ) и β(λ) трап ец еид ально й структуры с оцененными параметрами показаны на рис.4 непрерывными линиями. Сравнение расч етных и измеренных спектров демонстрирует хоро шую степень совпад ения спектров . Для оценки степени совпад ения спектров в эллипсометрич еских измерениях используется выборочный коэффициент корреляции (GOF). Для рассмотренного случ ая GOFα = 0, 966 и GOFβ = 0, 962 . Отличие в спектрах на рис.4 вызв ано неточностью модели. Изме-ря емая структура имеет профиль , отличный от идеального трапецеидального профиля.

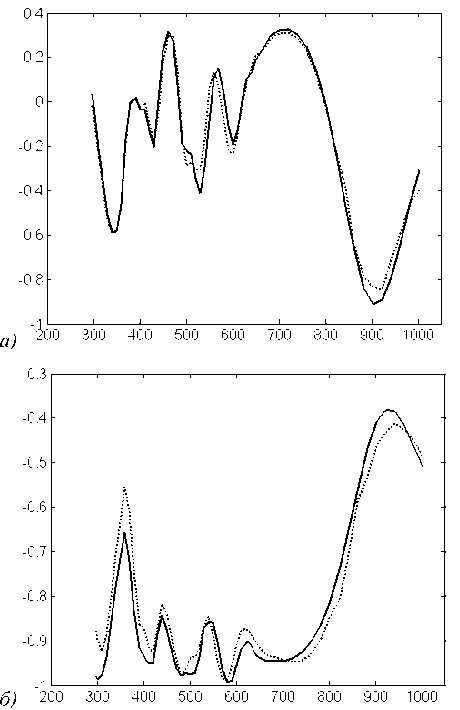
Рис. 4. Спектры α ( λ ) (а) и β ( λ ) (б) трапецеидальной решетки с оцененными параметрами.

Точечные линии – измеренные спектры, непрерывные – расчетные спектры

Заключение

Результаты численных экспериментов свидетельствуют о высокой точности предложенны х методов оценки параметров дифракционных структур. Математическая точность нахождения линейных параметров для обоих рассмотренны х методов выше 0,1 нм. Указанная точность превышает физически обоснованные требования. Скорость работы предложенных методов достаточна для выполнения около десятка измерений в сек унд у.

Результаты экспериментальных исследований демонстрируют применимость методов для реальных эллипсометрических измерений.

Предложенные методы очевидным образом допускают обобщение на задачи идентификации профиля с большим числом параметров.

Работа выполнена при поддержке российско-американской программы «Фундаментальные исследования и высшее образование» (BRHE), гранта Президента РФ поддержки вед ущих научных школ (НШ-3086.2008.9), грантов РФФИ № 07-01-96602, 07-07-91580, 08-07-99005, 09-07-92421 и Фонда содействия отечественной науке.