Определение параметров регуляторов в управляемой электромеханической системе на основе спектральной модели в базисе функций Чебышева-Лежандра

Современные ЭМС горных машин представляют собой сложную многокомпонентную совокупность взаимодействующих подсистем и элементов различной природы. Динамические характеристики ЭМС большинства горных машин под воздействием внешних факторов приобретают свойства изменчивости, что в значительной степени определяется условиями эксплуатации оборудования, характером нагрузок в ЭМС, а также специфическими свойствами технологических процессов работы оборудования. В то же время исследователи и разработчики ЭМС и систем управления ими должны быть обеспечены достоверными данными о динамических характеристиках ЭМС.

Таким образом, научное обоснование нового математического и алгоритмического обеспечения для разработки нового класса математических моделей ЭМС горных машин является актуальной научной проблемой.

При использовании метода разложения ИПХ в базисе СПООФ Чебышёва–Лежандра коэффициенты разложения ИПХ определяются в соответствии со следующим выражением:

X i = J h₅ (О Pto ⁽ u , t ) d-

h я О")

где     ^      - импульсная переходная характеристика идентифицируемой динамической системы.

При этом ИПХ идентифицируемой ЭМС может быть представлена следующим рядом [1, 2]:

hs(т) = txjP(u, t)• j 0             .                       (2)

Учитывая, что [3-8]

P_w ( u , t ) = (-1) ⁿ Ju (2 n + 1) t n + 12

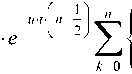
(1 -eu'*)k t (k + \)^_-Г{ П-к + 1)2

Можно получить общую формулу для ортогональной спектральной

модели ИПХ:

h₅ (0 = ^ Xj (-1) ^j V u (2 j + 1) Г j + 12 j= о

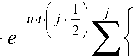
к =0

(1- e^u ) ^k

Г ( к +1) 2- Г ( j-k +1) 2

ut

= e ² £ Xj (-1) j V u (2 j + 1) Г j + 12

j =0

у I         (1- eu't)k to I г (к+1)2- Г( j-k+1)^2

В тоже время, так как [3-8]

Pn , ( u , t ) = (-1) ⁿ V u (2 n + 1) tn + 12

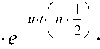
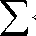
k =0

_________________1________________

Г ( k + 1) t(n-k + 1)2

у    (-1) ^j eut'j

"2-. Г ( j + 1)Г(k-j + 1)

о

h8 (т) = ^ Xj (-1)j 7u(2 j + 1) Г j +1Z j=o ut

= ^{e 2} ^Xj 2¹) j T u c j -i) Г j +1 Z • j =o

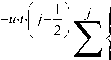
__________________1__________________

Г ( k +1) 2 Г ( j-k +1) 2

k =0

^j _eutj

k =0

__________________1__________________

Г ( k +1) 2 Г ( j-k +1) 2

i =0

(-1) j e uti i! ( k-i ) !

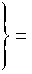
^k           j uti

⁽~¹⁾⁷ e

£0 ^i! ( ^k-i ) !

Для модели на основе первых трех функций Чебышёва–Лежандра можно записать следующее выражение:

ut hgз(t, u) = Z0 Vue 2

(      1              3

ut        ut

■t % 1V3 u e ²   -2 e²

(    1

ut

+ x₂'J5u e ²

ut

- 6 e ²

ut

+ 6 e ²

•

Установим выражение для операторной модели в пространстве преобразования Лапласа:

u

/—         V 3 up

„_г , X           u .             V 2 J . ГТ"

W 3⁽ P ) = Xo-----+ Z\ 7-----v----.   + Z2 V5 u

, u       (      u Y      3 )

p    p  pu

2      I     2A     2 J

u p" 2

pu

3 pu

3 Y

u

p up

2 A 2

•

Таким образом, изображение n-ой функции Чебышёва–Лежандра по

Лапласу можно определить следующей формулой:

п"Г Г (     2i + 1 )

4-1 I | pu

A z2 J

L T f_№ ( u , t ) = 7 u (2 n + 1)---- n^⁰-------------

П(   2i +1)

pu 2 i=0 v7

или

1 2 p-u + 2un

1 2 p-u- 2un

L TP n ^ ( u , t ) _= (-1) ⁿ 2 4u (2 n + 1)    ------------

J ( 2 u

12 p-u A

2 u )

.

Подставляя в формулу для нахождения коэффициентов разложения ИПХ (1) выражение, определяющее СПООФ Чебышёва-Лежандра (3), получим

Z = hs (f) P   (u, t) dx- nu           n^’

k

n

= (-1)n Г(n +1)2 Vu(2n + 1) У-------------------- t0 Г(k + 1)2Г(n-k + 1)2 j0

(-1) ^j Г(k + 1)   f, _ix-« ( n ₊1- jjr

-- — ----------- h (Лe    2

Г(j + 1)Г(k-j + 1)J

В соответствии с интегралом Лапласа запишем

00                      z 1.

С         - u (n+—-j )г.

h5 (г) e     2 dT = W (p)       1

J                                 p₌u ( n+—j )

о

На следующем этапе преобразований с учетом (6) и (7) установим зависимость, связывающую компоненты спектральной характеристики ИПХ в базисе СПООФ Чебышёва–Лежандра с параметрами передаточной функции ЭМС

n

Xnu = (-1)n Г(n +1)2 7u(2n + 1)£ k=0

k

(-1) j

Г ( k +1) Г ( n-k +1)² ^ j j + 1)Г( k -j +1)

W ( P )|   .  1 V

¹ P=u ( n+--j )

²     (8)

Из выражения (8) определим первые пять коэффициентов разложения ИПХ + u :

^ 0u

₂ I’   ^Xu

I—        i 3    1 f и 1

3 u - 2W\ - u\-W\- \ ’

12 Ш

^ 2 u =

5  к 3 к и к

5 u - 6- W -u -6- W — u +W -   ’

I2       12 J   Ш

^ 3 u="'

У • 20 • W - u - 30 • W ⁵ u | +12 • W ^- u - w| ^u

’

Хл  =V u - 210 - W -u -420 - W -u +270 - W -u -60- W -u +3- W -   .

a 4 u ^v        i^i      i^i      i^i     i^i i^i

Объединяя установленные выражения (9) в систему и решая ее wM W^wf относительно значении передаточной функции в узлах v2,   2 ;, к 2 ;,

W

, получим:

u       0         3u       1   3  1   3  0         5u      1    5  2   10  0   5  3

2     u       2      6      u           2    30

7u      1   7  5 2  35  0  21  3 1    7

• 2     140                 u

9u      1  12  5 2  42 0  28  3 1  3  7 34

.

• 2    140

Предполагая, что объект управления описывается передаточной функцией

W 0

k ₀

1   T 0 p

,

тогда пропорционально интегральный (ПИ) -регулятор можно описать передаточной функцией

W р ( p )     p

_p p 1

p ^p

Для расчётов параметров регулятора составим систему уравнений k0         0

1 T ^{u u} 0₂

k ₀          1

31    30

1 T ^{3 u     6}

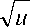
В итоге выполнения расчётов системы уравнения получаем значения: 6( x ₀) ²    2 3 x ₀ x ₁

k ₀

3V и • х₀ - 3V3V u X

6x0   23

T ₀

3u x 33

Подставляя данные значенияв формулу передаточного коэффициента регулятора и получаем[9]:

T           (3 u x 3 3 u x ) (2 3 x1   6

^p   2 T k 0    2(3 ux 3   3 u x ) [6 ( x ) ²   2 3 x x ] T

При помощи приведённых зависимостей можно произвести настройку на оптимум с применением ПИ-регулятора.

Аналогично можно определить параметры пропорционально-интегрально-дифференциального (ПИД) – регулятора, иммеющего передаточную функцию

Wр ( p ) =рp

p 1 ^p +¹ p 2 ^p +¹ p 1 ^p

Тогда система аналитических уравнений имеет вид:

к к 0102

X 0 u ^;

( T 01 ^u + 1)( T 02 ^u + 1)

k 01 k 02               1 .1 ³ X 1 3 X 0

(T01 3u + 1)(T02 3u- + 1)     6

k01k02           1.15^2+ 101053

(T01 5u + 1)(T02 5u + 1)   30

Решив систему уравнений и подставив полученные значения в формулу (14) получим зависимость для настройки на оптимум при помощи ПИД-регулятора для ЭМС определяемой СПООФ Чебышёва–Лежандра.