Определение параметров собственных тепловых импедансов силовых кристаллов IGBT-модуля

В настоящее время преобразователи частоты, применяемые в составе электропривода, как правило, строятся на основе силовых полупроводниковых приборов (СПП) модульной конструкции. Такое решение имеет множество преимуществ с точки зрения надёжности, экономической эффективности и качества конечной продукции. Устройства, используемые в составе модуля, подобраны по электрическим и тепловым характеристикам уже на заводе-изготовителе и оптимизированы для работы в конкретной области применения.

Для повышения надёжности электропривода в современные системы управления встраиваются тепловые модели силовых ключей. Применение тепловых моделей позволяет предсказать температуру полупроводникового прибора, оценить тепловой режим его эксплуатации и, в случае предельных нагрузок, предотвратить выход из строя электронного ключа и обмотки электродвигателя [1].

Достаточно часто подобные модели разрабатываются на основе метода электротепловой аналогии. Данные модели имеют множество достоинств, наиболее важные из которых это приемлемая точность расчёта температуры, низкие требования к вычислительным ресурсам устройства, возможность интегрирования тепловой модели непосредственно в систему управления [2; 3].

Однако электротепловая аналогия не лишена недостатков. Одним из постулатов данной теории является линейное распространение тепла. Таким образом, применение данных тепловых моделей в классическом виде ограничено теми областями, где основной тепловой поток распространяется в одном направлении от источника потока к радиатору. Такое распространение теплового потока наблюдается в дискретных СПП. Однако в модульной конструкции тепловые потоки от силовых кристаллов распространяются не только в сторону охладителя, но также части потоков распространяются в направлении соседних кристаллов, тем самым влияя на их тепловой режим.

Построение тепловых моделей в данном случае связано с определёнными трудностями. Необходимо точно знать физические параметры элементов конструкции, встречающихся на пути теплового потока, их геометрический размер, материалы и свойства, а также величину дополнительных тепловых потоков от соседних элементов. Данные параметры определить очень сложно в виду нелинейности распространения тепла. Кроме того, сложность теоретических расчётов существенно возрастает, поскольку одни и те же элементы конструкции в разной степени нагреваются разными приборами локально.

Поскольку каждый кристалл силового модуля имеет собственный путь отвода теплового потока, а элементы, через которые он проходит, нагреваются не равномерно, то для определения температуры полупроводниковых приборов было решено синтезировать собственную конфигурацию тепловой модели на базе RC-цепей типа Foster. Она изображена на рисунке 1.

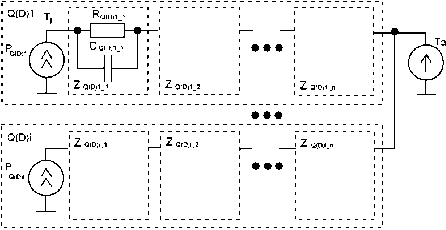
Рис. 1. Линейная электротепловая модель силового модуля.

Данная тепловая модель основывается на дискретном представлении полупроводниковых приборов, где каждый кристалл в составе модуля представляется отдельным элементом и имеет собственную линейную тепловую модель. Поскольку тепловые потоки от разных кристаллов проходят через одни и те же элементы конструкции, то они могут быть представлены несколькими RC цепями в разных тепловых моделях, и иметь разную локальную температуру. В связи с этим нет необходимости рассчитывать тепловое сопротивление и тепловую ёмкость для каждого элемента конструкции, достаточно чтобы их общая переходная характеристика теплового сопротивления кристалл-атмосфера, соответствовала переходному процессу для отдельного кристалла.

Недостатком данного подхода является невозможность прогнозирования температуры промежуточных элементов конструкции, таких как припой, медная подложка, изолятор, алюминиевое основание, радиатор. Данная тепловая модель не предполагает прямого переноса тепловой энергии от одного кристалла к другому, однако она учитывает влияние силовых элементов на путь распространения тепла в объёме общих подложек, основания и радиаторе. Теоретически рассчитать соотношение переданного тепла несколькими кристаллами достаточно сложно, поэтому был сделан вывод о необходимости определения тепловых потоков с помощью современных средств трёхмерного моделирования.

Программный продукт ANSYS Mechanical 17.0 позволяет определить как распространяется тепло в IGBT-модуле методом конечных элементов. В качестве исследуемого образца был выбран силовой IGBT модуль PS22A78-E, который представляет собой трехфазный инвертор, содержащий шесть IGBT-транзисторов и шесть обратно включённых силовых диодов. Внешний вид модуля и электрическая схема соединений СПП в модуле представлены на рисунке 2.

+^DC

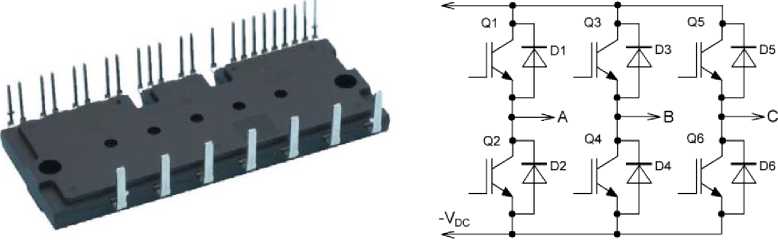
Рис. 2. Внешний вид модуля и электрическая схема соединений СПП в модуле.

На основе конструкции модуля была построена трёхмерная модель основных конструктивных элементов, через которые распространяется тепловой поток. В преобразователе силовой модуль является единой тепловой системой с его охладителем.

Поэтому исследование тепловых режимов IGBT-модуля проводилось совместно с его системой охлаждения. Разработанная трёхмерная модель представлена на рисунке 3. Геометрические размеры, соотношения между элементами, их взаимное расположение и материалы, используемые в модели, соответствуют реальной конструкции.

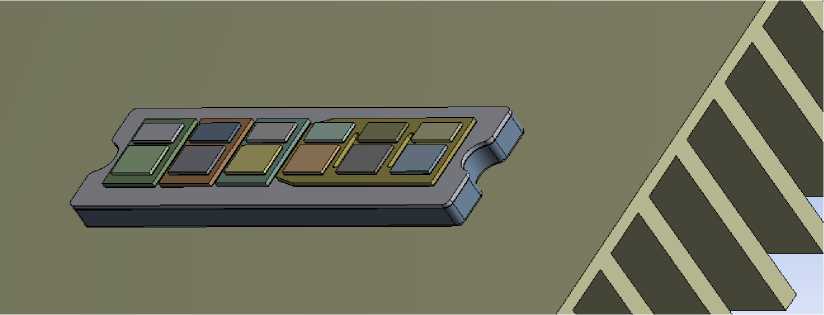
Рис. 3. 3D-модель IGBT-модуля c радиатором в ANSYS.

Для исследования тепловых эффектов в цифровой среде важной частью задачи было определить наиболее значимые граничные условия, являющиеся физическим обоснованием данной трёхмерной модели [4]. Были приняты следующие условия проведения эксперимента:

• –    источником нагрева является поток тепла постоянной мощности, эквивалентный мощности потерь, выделяемой на элементе в процессе работы электрической схемы;

• –    тепловой поток приложен к верхней грани силового кристалла и распространяется в сторону охлаждаемых элементов;

• –    вся поверхность радиатора, контактирующая с атмосферой, является излучателем конвекционного типа с величиной излучения 5·10^-6 Вт/мм², что соответствует естественной конвекции с воздухом;

• –    все остальные элементы конструкции покрыты компаундом, и величина излучения через компаунд пренебрежительно мала;

• –    температура, измеряемая на каждом элементе, отражает максимальное значение температуры в объёме, так как именно максимальная температура, будет сказываться на аварийных режимах работы СПП.

Определение величин теплового импеданса кристалл-атмосфера осуществлялось с помощью трёхмерной модели в среде ANSYS. Процедура определения заключалась в следующем. Поскольку для передачи тепла из одной области в другую необходима разность температур, необходимо было создать единственный тепловой поток кристалл-атмосфера и исключить обмен тепла между кристаллами соседних СПП. Это достигалось в 2 этапа. На 4

первом этапе кристаллы были нагреты до одинаковой температуры внешним источником постоянной температуры, и был измерен тепловой поток, проходящий через каждый элемент в сторону радиатора в установившемся режиме. На втором этапе кристаллы выступали в качестве нагревателя. Мощность потерь постоянной величины, выделяемая на них для достижения одинаковой температуры, была измерена в предыдущем опыте. Таким образом, был получен переходной процесс температур кристаллов в условиях постоянного нагрева соседей. Тепловой импеданс для каждого кристалла в каждый момент времени был рассчитан по формуле

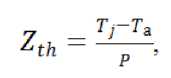
где Zth – собственный тепловой импеданс кристалла, Tj – температура нагреваемого кристалла, Ta – температура атмосферы, P – мощность потерь, вызывающая нагрев до температуры Tj.

Полученные зависимости теплового импеданса представлены на рисунке 4.

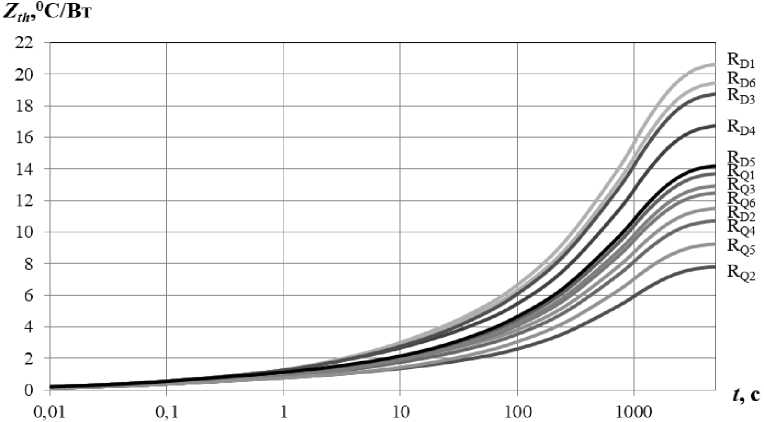
Рис. 4. Переходные тепловые сопротивления кристалл-атмосфера СПП.

Для перехода к тепловой модели на основе электротепловой аналогии используем аппроксимацию временных зависимостей собственных тепловых сопротивлений. Для аппроксимации используем функцию переходного процесса для RC цепи n-го-порядка

Z,h(t)=x".1 Rth,(l-e~’^

где R th – тепловое сопротивление в установившемся значении;

Т ^ = R th C th - тепловая постоянная времени, где C ^ - теплоёмкость.

Параметры уравнения аппроксимации (2) находились автоматически с помощью 5

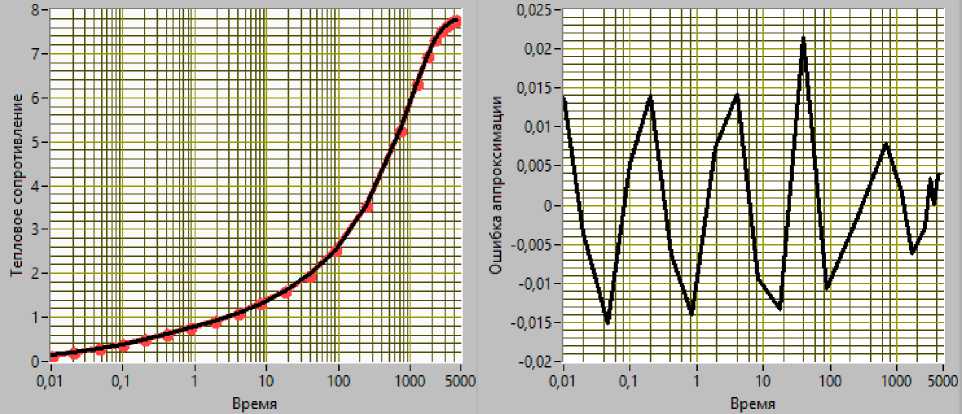
программного комплекса LabVIEW. На рисунке 5 представлены результаты аппроксимации теплового импеданса одного из кристаллов.

(а)

(б)

Рис. 5. Переходные тепловые сопротивления кристалл-атмосфера СПП.

На рисунке 5 a входные данные моделирования отображены в виде красных точек, чёрной линией показана функция аппроксимации с подобранными коэффициентами. На рисунке 5 б изображена абсолютная ошибка аппроксимации.

Полученные параметры функции аппроксимации приведены в таблице 1.

Таблица 1

Параметры функции аппроксимации

Z	R1, 0С/Вт	C1, Дж/0С	R2, 0С/Вт	C2, Дж/0С	R3, 0С/Вт	C3, Дж/0С	R4, 0С/Вт	C4, Дж/0С	R5, 0С/Вт	C5, Дж/0С	Rмакс, 0С/Вт	Cобщ, Дж/0С
Q2	0,260	0,071	0,431	0,679	0,625	9,190	0,987	74,155	5,518	167,582	7,821	1,674
D2	0,330	0,041	0,626	0,424	0,905	5,643	1,483	46,535	8,182	112,839	11,527	2,609
Q4	0,271	0,071	0,459	0,858	0,947	6,173	1,432	49,050	7,632	120,718	10,741	1,427
D4	0,385	0,044	0,714	0,588	1,453	4,095	2,249	31,473	11,966	77,136	16,767	2,033
Q6	0,298	0,077	0,434	1,075	1,111	5,736	1,760	39,960	8,912	103,580	12,515	1,217
D6	0,458	0,053	0,777	0,918	1,719	4,670	2,638	28,599	13,901	66,602	19,493	1,407
Q1	0,309	0,077	0,484	1,162	1,170	6,000	1,969	36,107	9,805	94,099	13,737	1,143
D1	0,448	0,053	0,761	0,864	1,803	4,357	2,939	26,029	14,742	62,903	20,692	1,495
Q3	0,318	0,081	0,520	1,115	0,995	7,343	1,913	37,371	9,218	100,116	12,964	1,150
D3	0,375	0,046	0,710	0,570	1,503	4,203	2,796	24,776	13,406	68,732	18,790	2,093
Q5	0,252	0,070	0,432	0,678	0,632	9,702	1,391	48,093	6,559	140,102	9,266	1,676
D5	0,339	0,043	0,626	0,446	0,960	5,640	2,174	30,166	10,121	90,588	14,220	2,505

Экспериментальным способом было установлено, что наилучшая аппроксимация достигается при использовании значени n = 5. В этом случае среднеквадратическое отклонение полученной функции от исходных данных моделирования составляет 0,0005, а количество параметров тепловой цепи не замедляет расчёт температуры. Аппроксимация данной функции обладает наибольшей сходимостью при начальных значениях теплоёмкости представленных числами различных разрядов, а начальные значения тепловых сопротивлений равны максимальному значению теплового сопротивления, разделённому на порядок цепи.

Исходя из полученных данных, максимальное тепловое сопротивление достигается в конце переходного процесса и равно сумме тепловых сопротивлений входящих в состав RC-цепей. Общая тепловая ёмкость соответствует последовательному соединению ёмкостей. На рисунке 6 изображено трёхмерное представление линейных RC цепей для транзисторов и диодов. Максимальное тепловое сопротивление и общая тепловая ёмкость представлены графиком для кристаллов в соответствии с их физическим расположением в модуле.

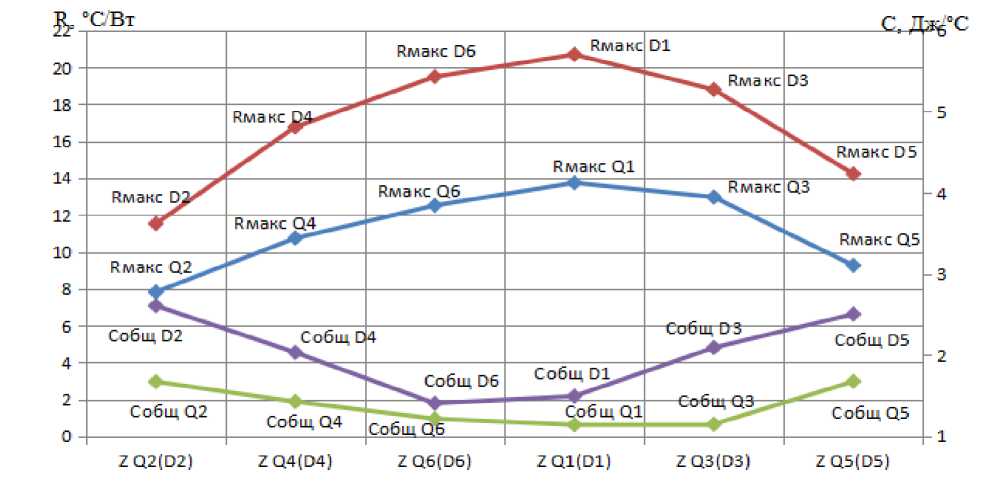
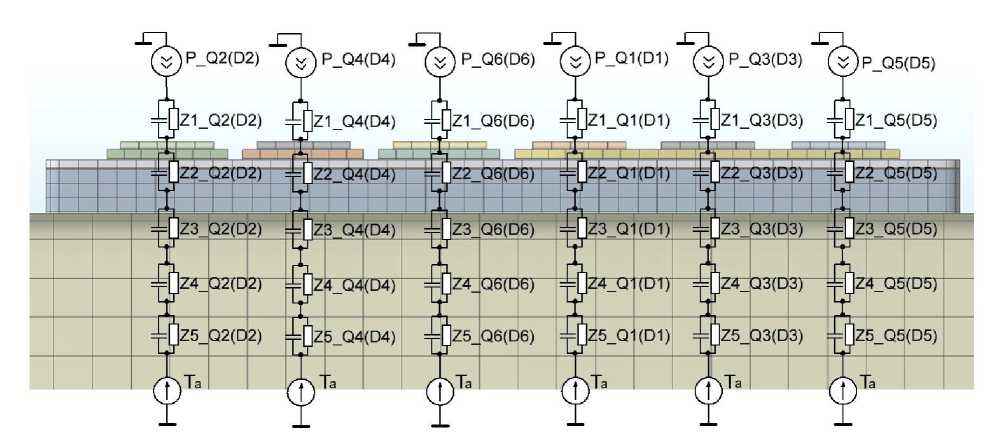
Рис. 6. Тепловые сопротивления и тепловые ёмкости в соответствии с представлением линейных электротепловых цепей на трёхмерной модели.

Таким образом, можно видеть, что собственные тепловые сопротивления полупроводниковых приборов сильно отличаются в зависимости от их расположения в силовом модуле, и даже если они имеют одинаковые электротепловые характеристики, они будут работать в разных тепловых режимах. Наиболее неблагоприятные условия работы будут у диода D1, который имеет наибольшее тепловое сопротивление кристалл-атмосфера, а, следовательно, хуже всего рассеивает тепло. Как видно из графиков, общее тепловое сопротивление диодов выше, чем тепловые сопротивления соответствующих транзисторов. Это связано с меньшей площадью поверхности диодов, через которую они выделяют тепло.

С другой стороны, центральные полупроводниковые кристаллы имеют наименьшую тепловую ёмкость. Это связано с тем, что область распространения тепла под этими кристаллами прогреется быстрее всего за счёт воздействия соседних кристаллов. А тепловая ёмкость кристалла D2 имеет наибольшее значение, поскольку с этой стороны имеется хороший отток тепла в виде большого радиатора.

В технической документации на данный модуль приведено значение среднего теплового сопротивления для транзистора и диода в устоявшемся режиме. Однако, как видно из исследования, параметры кристаллов СПП могут сильно отличаться в зависимости от положения в силовом модуле и их представления в тепловой модели. Предложенная тепловая модель и методика определения её параметров позволяет учесть эту разницу и точно определить тепловой режим полупроводниковых устройств.