Определение параметров уравнения Фогеля-Фульчера-Таммана для температурной зависимости вязкости в области перехода жидкость-стекло

Температурная зависимость вязкости жидкостей описывается уравнением Эйринга [1, 2]

П = П о exp

(J

I RT У

где Е_η – свободная энергия активации процесса вязкого течения жидкостей, η ₀ - предэкспоненциальный множитель, равный предельному значению вязкости при Т→∞, R – газовая постоянная.

У простых жидкостей (типа расплавов металлов) величина Е_η является постоянной величиной Е_η ≈ const, а у стеклующихся жидкостей (расплавов стекол, полимеров) оказывается функцией температуры Е η ( Т ) . Явный вид этой функции теорией не устанавливается.

В области стеклования жидкостей широкое распространение получило уравнение Фогеля-Фульчера-Таммана (уравнение ФФТ) [1, 2]

П = A exp I t

B

-

— I , T о J

где A , B и T 0 – эмпирические постоянные.

Из данных о параметрах B и T 0 можно рассчитать значение доли флуктуационного объема f g , замороженной при температуре стеклования T=T_g ,

T - T

T_g T ₀

.

fg B

Эта величина f_g является одним из важных параметров модели возбужденного состояния стеклообразных систем [3-5]. Флуктуационный объем жидкостей и аморфных сред обусловлен критическими смещениями возбужденных кинетических единиц (атомов, групп атомов), соответствующими максимуму силы межатомного взаимодействия [3-5]. Он тесно связан с молекулярной подвижностью в аморфных средах.

Данная работа посвящена определению параметров уравнения ФФТ и расчету f g для оптических стекол.

Методика расчета

Предэкспоненциальные множители η ₀ и А в уравнениях вязкости (1) и (2) практически равны и соответствуют вязкости веществ в газообразном состоянии [1, 2]

η ₀ ≅ А ≈ 10 ^{- 4} Па ⋅ с                                   (4)

Они определяются путем экстраполяции кривой lg η – (1/ T ) к значению Т→∞. Как правило, все кривые lg η – (1/ T ) при (1/Т)→0 сходятся в одной точке lg η ≈ -4.

Из сравнения уравнений вязкости (1) и (2) при условии (4) получаем следующую температурную зависимость свободной энергии активации вязкого течения

( т ¹

E = E I 1 - T X I , ^п \ T )

где E ∞ имеет смысл свободной энергии активации при повышенных температурах Т→∞

E∞ = RB                           (6)

При обработке экспериментальных данных соотношение (5) удобно представить в виде уравнения прямой

X = X -I T ) 1                          (7)

En   E- IЕ- ) Т и построить график в координатах (1/Еη) – (1/T), который должен представлять собой прямую, если зависимость (5) справедлива.

Величину (1/E∞) находим путем экстраполяции прямой к 1/T=0. Зная E∞ и определив тангенс угла наклона прямой А(1/Еп)/А(1/T), определяем параметр Т0

А(1/E„)

Ч_1

^{1 0} E ” А ( 1/ Т )

га

.

Параметр В вычисляется по формуле (6): B=E ∞ /R .

Значения свободной энергии активации вязкого течения при различных температурах Е η ( T ) определяется по уравнению вязкости (1)

E n = 2,3 RT ( lg n - lg П o ) ,                                    ⁽⁹⁾

где lgn о = const = -4. За T_g приняли температуру при 10¹⁵ Па - с.

Результаты расчетов и обсуждение

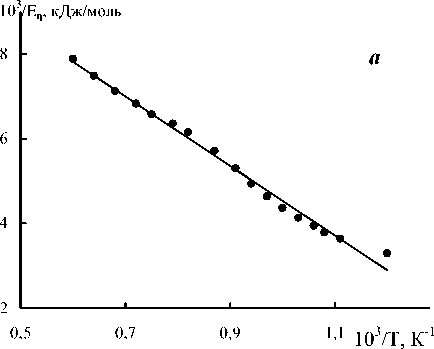
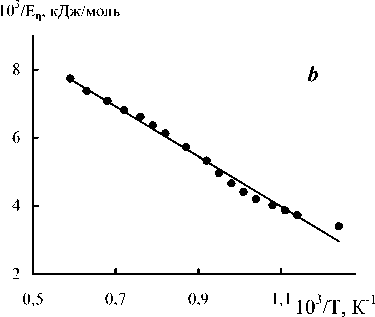
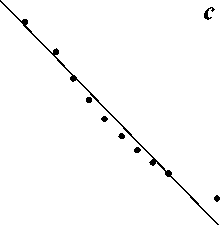
За объект исследований выбрали промышленные многокомпонентные оптические стекла [6-8]. Исходные экспериментальные данные о температурной зависимости вязкости стекол различных марок взяты из справочника [6]. Из этих данных по формуле (9) рассчитали свободную энергию активации вязкого течения Е_η ( T ) при различных температурах. Затем в соответствии с уравнением прямой (7) построили графики в координатах (1/ Е η )–(1/ T ). Для всех исследованных оптических стекол (табл.1) зависимость 1/ Е η от 1/ T оказалась линейной, что подтверждает применимость к этим стеклам уравнения ФФТ (2). В качестве примеров (рис.1 а-d) приводятся прямые (1/ Е_η )–(1/ T ) для ряда стекол (ТК116, БФ11, СТК3, ТФ10).

Таблица

Параметры уравнения Фогеля-Фульчера-Таммана (2) для оптических стекол

Марка стекла	T g , K ( lg n =15)	E n ( T g ), кДж/моль	E „ „ кДж/моль	T 0 , K	B , K	f g
ЛК3	667	242	133	320	16053	0,022
ЛК5	766	278	158	341	18965	0,022
ЛК6	585	212	155	160	18683	0,023
К8	741	269	104	471	12505	0,022
К14	748	272	126	377	15110	0,025
К17	757	275	110	460	13189	0,023
К19	733	266	129	389	15492	0,022
БК4	751	273	119	442	14364	0,022
БК10	774	281	100	525	12029	0,021
БК11	800	291	97	539	11687	0,022
ТК114	840	305	60	718	7271	0,017
ТК116	833	303	78	652	9341	0,019
ТК20	836	304	72	697	8630	0,016
ТК23	855	310	68	697	8176	0,019
СТК3	862	313	89	467	10731	0,037
СТК9	874	317	46	755	5510	0,022
ФК14	730	265	53	635	6422	0,015
БФ11	809	294	81	633	9760	0,018
БФ12	673	244	109	398	13079	0,021
ЛФ5	664	241	143	265	17237	0,023
ЛФ9	689	250	97	438	11718	0,021
Ф102	676	245	125	339	15015	0,022
ТФ1	643	234	120	317	14412	0,023

ТФ10	630	229	79	423	9551	0,022
ОФ1	658	239	104	306	12551	0,028
ОФ4	721	262	39	654	4719	0,014

10³/E _η , кДж/моль

0,8

1,2

103/Т, К-1

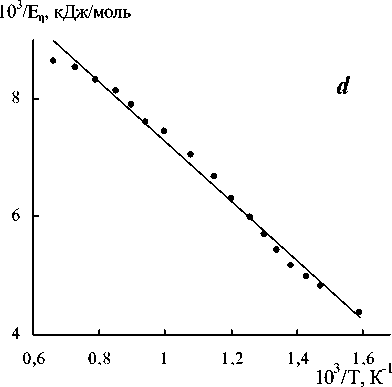
Рис. 1. Температурная зависимость свободной энергии активации вязкого течения в координатах соотношения (7). а – ТК116, b – БФ11, c – СТК3, d – ТФ10

По описанной выше методике из таких прямых определили параметры уравнения ФФТ и на их основе по формуле (3) рассчитали долю флуктуационного объема при температуре стеклования (табл.)

f. =

V f V

- const

- 0,020 * 0,023 .

T = T

g

Как и следовало ожидать, величина f g оказалась практически постоянной величиной (10), как и у других стеклообразных систем [3-5]. Вместе с тем для некоторых оптических стекол наблюдается отклонение от постоянства f g (10). Так, например, у особого флинта ОФ4 величина f g равна 0,014, а у флинта ОФ1 - f_g = 0,028 (табл.).

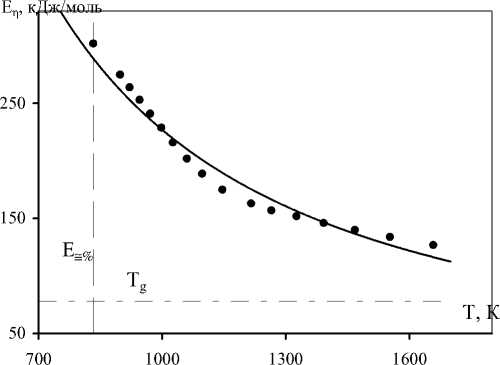
Рис. 2. Температурная зависимость свободной энергии активации вязкого течения оптического стекла ТК116

Рассмотренный способ определения параметров уравнения ФФТ находится в согласии с другими методами. Полученные значения Е_п при температуре стеклования ( - 250 ^ 300 кДж/моль) и E „ = 80 ^ 130 кДж/моль хорошо согласуются с имеющимися данными для многокомпонентных силикатных стекол [1, 2]. Также температурная зависимость Е_η( T ) оказывается вполне разумной (рис.2). При высоких температурах ( T > T g +200 K) свободная энергия активации вязкого течения перестает меняться с температурой ( E _n = const = E „ ) вследствие наступления предельного взаимодействия валентных связей [9, 10], а с точки зрения модели возбужденного состояния – вследствие достижения предельной концентрации возбужденных кинетических единиц, ответственных за вязкое течение [3-5]. При понижении температуры свободная энергия активации текучести возрастает из-за очевидного уменьшения концентрации возбужденных атомов (затухания процессов переключения валентных связей [9, 10]).

Таким образом, рассмотренный метод определения параметров уравнения ФФТ вполне оправдывается. На его основе можно рассчитать характеристики ряда моделей вязкого течения стеклообразующих жидкостей [3-5, 9, 10], что дает возможность высказать определенные суждения о природе текучести стекол и их расплавов в области перехода жидкость-стекло.

Работа выполнена при финансовой поддержке гранта БГУ « Лучшая научная школа ».