Определение погрешностей отклонений от линии пути при управлении судном по обсервациям двух разнесенных точек

Известен способ управления движением судна по величинам поперечных смещений двух точек, расположенных на диаметральной плоскости судна, например, носовой точки А и кормовой точки В. Эти смещения рассчитываются от текущего положения судна на траектории сближения. Для вычисления поперечных смещений точек А и В используются их координаты в неподвижной системе координат А ( X 0A , Y 0A ), В ( X 0B , Y 0B ) (рис. 1), измеренные с помощью спутниковой навигационной системы с дифференциальными поправками. Перекладку руля судна производят в зависимости от комбинации поперечных смещений носовой d A и кормовой d B точек судна относительно текущего положения на траектории сближения по закону а = - k A • d_A + k_B • d_B . Здесь k_A и k_B - коэффициенты усиления по этим управляемым параметрам.

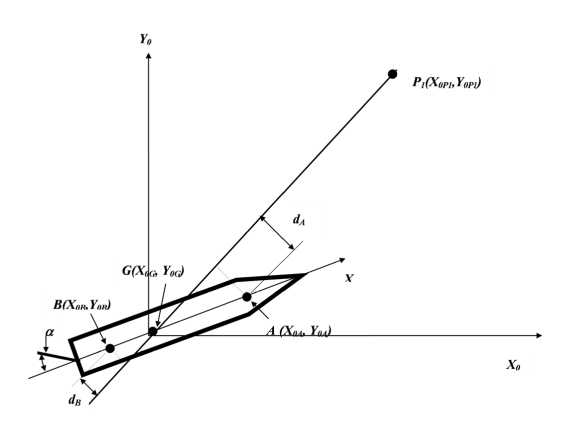
Рис. 1. Способ управления движением судна по отклонениям двух точек от текущей линии пути

Отклонения носовой и кормовой точек от текущей линии пути определяются следующими соотношениями:

d A = I ^[( Y 0A ^- Y 0G )'( X 0P 1 ^- X 0G ) ^{- (} X 0A ^- X 0G )*( Y 0P 1 ^- Y 0G ^)] I / ^[( X 0P 1 ^- X 0G ) 2 ^{+ (} Y 0P 1 ^- Y 0G ) ^2]0.5;

d B = ^{1 [(} Y 0B ^- Y 0G )'( X 0P 1 ^- X 0G ) ^{- (} X 0B ^- X 0G )*( Y 0P 1 ^- Y 0G ^{)] 1} / ^[( X 0P 1 ^- X 0G ) 2 ^{+ (} Y 0P 1 ^- Y 0G ^)2]0^.5 .

Используя указанные выражения, определить погрешности отклонений прямым методом представляется затруднительным ввиду сложной нелинейной зависимости от координат. Поэтому попытаемся оценить численно эти погрешности в зависимости от точности определения местоположения носовой и кормовой оконечностей судна.

• 2.    Вычисление погрешности определения координат центра тяжести судна

Вычисление координат центра тяжести судна в неподвижной системе координат осуществляется по формулам:

• Y 0G = Y 0A ^{- [(} Y 0A ^- Y 0B И X A ^- X G ^)]/( X A ^- X B ^);

X 0G = X 0A ^{- [( X}0A ^- X 0B И X A ^- X G ^)]/( X A ^- X B ).

Поскольку ( X_A - X_B ) = L - длина судна при разнесении антенн приемников GPS на оконечности судна, а ( X_A - X_G ) = K - фиксированная величина при данной загрузке судна, получаемая расчетным путем, можно упростить выражения для вычисления координат центра тяжести судна в неподвижной координатной системе:

Y 0G = Y 0A ^{- (} Y 0A ^- Y 0B ) ^{K /} L ^;

^X0G = ^X0A ^{- ( X}0A ^- X 0B ) ^{K /} L .

Математические ожидания координат X_0G и Y_{0G :}

M ( Y og ) = M ( Y oa ) - [ M ( Y oa ) - M ( Y ob )]• KIL ;

M ( X og ) = M ( X oa ) - [ M ( X oa ) - M ( X ob )]• KIL .

Отклонения координат X_0G и Y_0G от их математических ожиданий:

V Y0G = Y 0G ^{- M} ( Y 0G ) = V Y0A ^{- (} V Y0A ^- V Y0B ) K ^{/ L ;}

V X0G = ^X0G ^{- M} ( ^X0G ) = V X0A ^{- (} V X0A ^- V X0B ) K ^{1 L} -

Квадраты отклонений координат X_0G и Y_0G от их математических ожиданий:

V Y0G ² = V Y0A ^{2 + [} V Y0A ^- V Y0B ^]2 ^{K 2/ L} 2 ^- V Y0A ^[ V Y0A ^- V Y0B ^{] 2} K ¹ L = = V yoa ² ( L - K ) ² / L ² + V yoa V yob 2 KL ( L - K )/ L + V yob ² K ² L².

Применив операцию математического ожидания к обеим частям равенства, получим выражения для дисперсий координат:

D ( Y og ) = D ( Y oa ) ( L - K ) ² / L ² + D ( Y ob ) K 2 / L 2 ;

D ( X og ) = D ( X oa ) ( L - K ) ²/ L ² + D ( X ob ) K 2 / L ²

Определим корреляционный момент между координатами, исходя из определения корреляционного момента как математического ожидания от произведения отклонений:

M xyg = M { V yog V xog } =

= M ^{[ V YOA ^{- (} V YOA ^- V YOB )• ^{K / L ] [} V XOA ^{- (} V XOA ^- V XOB )• ^{K / L ]}} = = M xya ( L - K) ²/ L ² + M xyb K 2 / L 2 .

Для формирования эллиптической погрешности точки G, т.е. определения параметров ее эллипса погрешностей, воспользуемся известными формулами объединения двух векториальных погрешностей V1 и V2 в эллипс погрешностей (Абезгауз, 1970). В нашем случае формулы можно упростить, так как векториальные погрешности ортогональны, и угол 9 = 0. Тогда tg 2a = 2kV1 V2/(V1^ - V22);

a ² ( b ² ) = 0.5{( V 1 ² + V 2 ² )+[( V 1 ² - V 2 ² ) ² + (2 kV1 V 2) ² ] ^1/2 }.

Найденные нами выше дисперсии координат точки G и есть квадраты объединяемых векториальных погрешностей, а корреляционный момент есть произведение коэффициента корреляции и векториальных погрешностей:

D ( X og ) = V 1 2 , D ( Y og ) = V 2 ² , M xyg = kV1 V 2.

Следовательно, искомые параметры эллипса погрешностей (ориентация и размеры) точки G можно выразить в терминах дисперсий и корреляционного момента в этой точке:

tg2 a = 2 M xyg / ( D ( X og ) - D ( Y og ));

a ² ( b²) = 0.5{( D ( X og ) + D ( Y og )) + [( D ( X og ) — D ( Y og )) ² + (2 M xyg )T}.

Обозначим для обсервованных точек A и В a 0A , b 0A , α 0A и a 0B , b 0B , α 0B - полуоси эллипса погрешностей и угол наклона его большой оси. Для каждой из этих точек можно записать набор соотношений:

2 M XYA = tg2 α A [ D ( X OA ) – D ( Y OA )] = tg2 α A cos2 α A ( a OA ² - b OA ² ) = ( a OA ² - b OA ² )sin2 α A ;

D ( X OA ) = ( a OA ² + b OA ² + cos2 α A ( a OA ² - b OA ² ))/2;

D ( Y OA ) = ( a OA ² + b OA ² – cos2 α A ( a OA ² - b OA ² ))/2.

Аналогичные выражения можно получить и для точки B . Теперь можно определить характеристики эллипса погрешностей, связанного с точкой G :

2 M_XYG = ( a_OA ² - b_OA ² ) sin2 α _A ( L – K ) ² / L ² + ( a_OB ² - b_OB ² ) sin2 α _BK ² / L ² ;

D ( X_OG ) + D ( Y_OG ) = ( a_OA ² + b_OA ² )( L – K ) ² / L ² + ( a_OB ² + b_OB ² ) K ² / L ² ;

D ( X_OG ) - D ( Y_OG ) = ( L – K ) ² /2 L ² cos2 α _A ( a_OA ² - b_OA ² ) + K ² / L ² cos2 α _B ( a_OB ² - b_OB ² ).

Мы получили все выражения, достаточные для определения характеристик эллипса погрешностей, связанного с точкой G . Пример расчета характеристик эллипса погрешностей представлен ниже для следующего случая (погрешности в метрах, углы в градусах):

Параметры эллипса носовой точки - a_A = 7, b_A = 5, α _A = 25.

Параметры эллипса кормовой точки - a B = 6, b B = 8, α B = 30.

Результаты расчета параметров эллипса для точки G приведены в таблице для различных величин ( X A – X G ) = K . Вычислением проверены формулы, которые в частных случаях точек A ( K =0) и B ( K = L ) дают характеристики эллипсов погрешностей именно этих точек.

K	L/4	L/2	3L/4	0	L
α G	24	-38	30	25	30
a G	5.4	4.7	6.1	7	6
b G	4.2	4.5	4.8	5	8

3. Вычисление погрешности отклонений от заданной линии движения

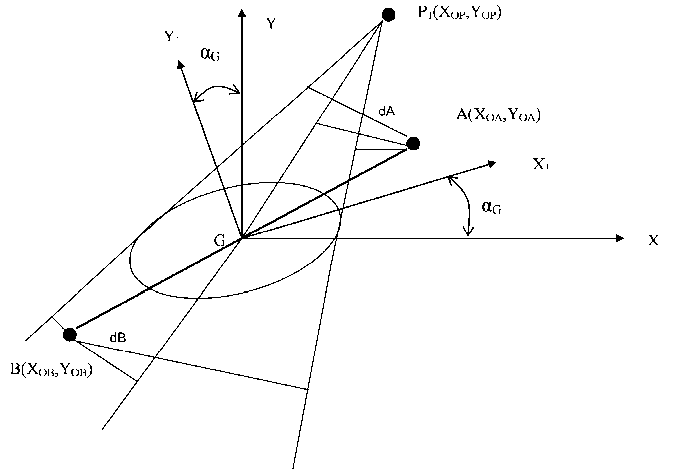
Рис. 2. К вычислению погрешности отклонений от текущей линии пути

Координаты заданной точки Р 1 ( X OP , Y OP ) в неподвижной системе координат GXY нам известны. Для преобразования этих координат в систему GX 1 Y 1 , связанную с осями найденного ранее эллипса погрешностей точки G (рис. 2), можно воспользоваться простыми соотношениями:

X_{OP 1} = X_OP cos α_G + Y_OP sin α_G ;

Y_{OP 1} = - X_OP sin α_G + Y_OP cos α_G .

Аналогично, для носовой точки судна A ( X OA , Y OA ) и кормовой B ( X OB , Y OB ) можно выполнить преобразования координат в систему GX ₁ Y ₁:

X_{OA 1} = X_OA cos α_G + Y_OA sin α_G , X_{OB 1} = X_OB cos α_G + Y_OB sin α_G ;

• Y_{OA 1} = - X_OA sin α_G + Y_OA cos α_G , X_{OB 1} = X_OB cos α_G + Y_OB sin α_G .

Запишем уравнение прямой Р ₁ G в виде уравнения прямой, проходящей через две точки Р ₁( X_OP , Y_OP ) и G ( X_{OG 1}, Y_{OG 1}):

( X 1 – X OG 1 )/( X OP 1 – X OG 1 ) = ( Y 1 – Y OG 1 )/( Y OP 1 – Y OG 1 ).

Из канонического уравнения эллипса можно получить следующее соотношение:

YOG1 = (bOG / aOG)(aOG2 – XOG12)0.5, где -a0G < X0G1 < a0G; aOG и bOG – параметры эллипса погрешностей точки G.

Подставляя это выражение в уравнение прямой, проходящей через две точки, можно получить ряд уравнений, определяющих пучок прямых, исходящих из точки Р 1 ( X OP 1 , Y OP 1 ) и проходящих через вероятное местоположение точки центра тяжести судна G ( X OG 1 , Y OG 1 ) .

X1 d1+ Y1 d2+ d3 = 0, где d1 = YOP1 – (bOG /aOG)(aOG2 – XOG12)0.5, d2 = XOG1 – XOP1 , d3 = XOP1(bOG /aOG)(aOG2 – XOG12)0.5 – XOG1YOP1.

Для определения среднеквадратической погрешности отклонений от линии пути используем две прямые, являющиеся касательными к эллипсу погрешностей (линии наибольших отклонений), и прямую, проходящую через центр эллипса (наиболее вероятнейшее местоположение центра тяжести судна).

Расстояния от точек A ( X OA 1 , Y OA 1 ) и B ( X OB 1 , Y OB 1 ) до прямой определяются соотношениями:

d A = |( d 1 X OA 1 + d 2 Y OA 1 + d 3)/( d 1 ² + d 2 ² ) ^0.5 |;

d B = |( d 1 X OB 1 + d 2 Y OB 1 + d 3)/( d 1 ² + d 2 ² ) ^0.5 |.

Таким образом, мы получили выражения для определения величины отклонений носовой и кормовой оконечностей судна от текущей линии пути, связанные с параметрами эллипса погрешностей места судна (центра тяжести). Погрешность в управляющем сигнале на отклонение руля находится в линейной зависимости от СКП отклонений точек от заданной линии пути Δ α = - k A ∙Δ d A + k B ∙Δ d B .

Приведем пример численного расчета:

Параметры эллипса точки центра тяжести - a OG = 10, b OG = 7, α OG = ±45º.

Координаты заданной точки Р 1 (50, 50).

Координаты точек А (25,15) и B (-25,-15).

α OG	-45º	-30º	-15º	0º	15º	30º	45º
d A max	13.0	12.8	12.4	12.0	11.8	11.5	11.2
d A min	1.0	1.0	1.5	1.6	2.0	2.5	2.9
СКП d A	6.0	5.9	5.5	5.2	4.9	4.5	4.2
d B max	7.0	6.5	5.6	4.6	4.2	3.4	2.7
d B min	21.0	-20.9	-20.0	-19.6	-18.7	-17.7	-16.7
СКП d B	14	13.7	12.8	12.1	11.5	10.5	9.7

Очевидно, что кормовая точка, находящаяся за эллипсом погрешностей, будет иметь большую величину погрешности. Равенства СКП можно достичь, увеличивая дистанцию до заданной точки, либо выбором точки G , относительно которой производится управление, ближе к кормовой оконечности судна.

Изменяя положение заданной точки Р 1 на заданной линии пути, т.е. меняя расстояние между центром тяжести судна и заданной точкой при тех же параметрах эллипса погрешностей, можно убедиться, что СКП отклонения от заданной линии движения (рис. 4) зависит от дистанции до заданной точки. То есть, при использовании способа управления по отклонениям двух разнесенных точек объекта от заданной линии движения, при сближении с заданной точкой вплотную точность определения отклонений уменьшается. Чтобы исключить зависимость увеличения СКП отклонений от линии движения при уменьшении расстояния до заданной точки, предлагается использовать способ "условно" заданной точки, который заключается в следующем:

За промежуток времени Δ t судно приблизилось к заданной точке P 1 (рис. 5). При этом новые координаты точки центра тяжести судна G ′ ( X ′ 0G , Y ′ 0G ) изменились относительно старых координат на некоторые величины Δ X и Δ Y

X’_0G = X_0G + Δ X₀ ;

X’_0G = X_0G + Δ Y₀ .

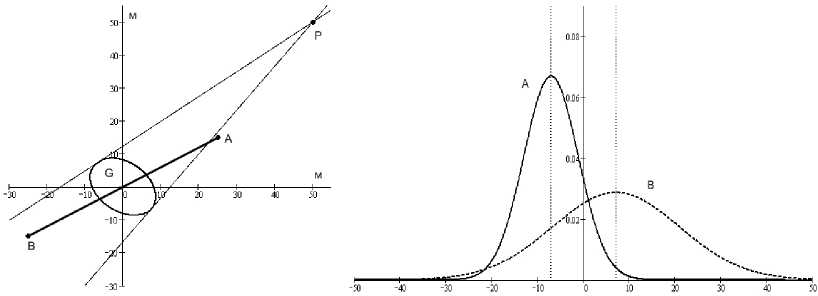
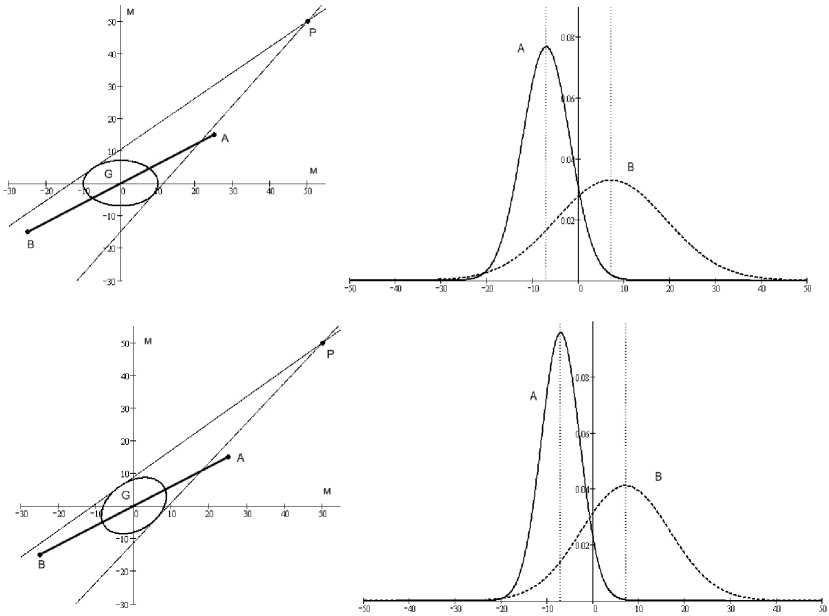
Рис. 3. Отклонения носовой и кормовой точек от текущей линии движения при различных углах наклона большой полуоси эллипса погрешностей a _OG = - 45°, a _OG = 0°, a _OG = 45° и графики распределения вероятности отклонений носовой А и кормовой В точек от линии движения

Продолжим линию за точку Р ₁ до некоторой условной точки Р '₁( Х'_0РbY'_{0P 1}), такой, что:

^Х0р 1 = Х 0Р 1 ^{+ AX}0 ^;

Y'op i = Y'op i + A Y o .

Будем считать ее новой условно заданной точкой и будем выполнять сближение с ней. Соответственно, отклонения кормовой и носовой точек будем рассчитывать относительно этой условной точки:

d A = I ^[( Y 0A ^- Y 0G )'( X 0P 1 ^- X 0G ) ^{- (} X 0A ^- X 0G )'( Y 0P 1 ^- Y ' oG ^)] / ^[( X 0P 1 ^- X 0G ) 2 ^{+ (} Y ' OP 1 ^- Y ' oG ^l^;

d B = I [( Y ob — Y og )•( X'op 1 — X ' og ) — ( X ob — X ' og )•( Y' op 1 — Yog )] / [( X op 1 — X 0g ) ² + ( Y op 1 — Y og ) ² ] ^0.5 .

Использование перемещения условно заданной точки позволяет сохранять погрешность вычисления отклонений d A и d B на одинаковом уровне, на всем пути сближения до заданной точки, в том числе и при сближении с ней вплотную.

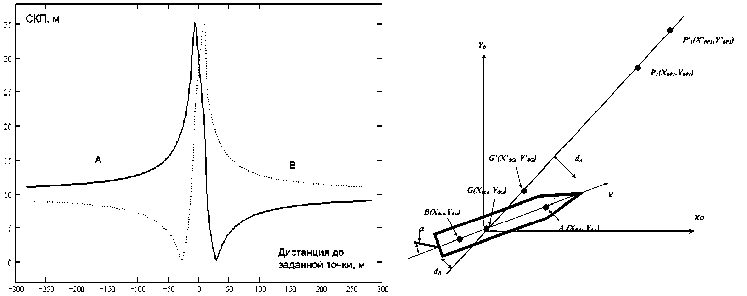
Рис. 4. Зависимость СКП отклонений точек А и В от линии пути в зависимости от дистанции до заданной точки

Рис. 5. Способ "условно" заданной точки

4. Заключение

При оценке среднеквадратической погрешности отклонений носовой и кормовой точки от заданной линии пути по данным DGPS для них при управлении судном по величинам этих отклонений можно построить зависимость между ними и параметрами эллипсов погрешностей этих двух точек. Эта зависимость геометрически представляет собой пучок прямых, проходящих через заданную точку, и вероятные места определения координат центра тяжести судна. Касательные, проведенные из заданной точки к эллипсу погрешностей, будут давать максимальные отклонения от вероятнейшего положения центра тяжести судна. СКП этих отклонений зависят от ориентации эллипса погрешностей центра тяжести и дистанции до заданной точки. При управлении судном по величинам отклонений от линии пути можно использовать перемещаемую "условно" заданную точку, когда расстояние между центром тяжести судна и заданной точкой остается постоянным на всем пути движения.