Определение погрешности измерения радиуса кривизны сферического вогнутого зеркала с помощью лазерного дальномера

В настоящее время широкое распространение получили измерительные приборы с датчиками волнового фронта (ДВФ) [1].

Основным измеряемым параметром для ДВФ является радиус кривизны волнового фронта, который может использоваться как для определения расстояния до источника излучения, так и для измерения кривизны поверхности оптических деталей [2–6].

Для измерения больших расстояний (радиусов кривизн волнового фронта) ДВФ необходима калибровка с помощью высокоточного лазерного дальномера, поскольку известные методики измерения радиуса кривизны достаточно трудоемки [7, 8] и занимают большое количество времени, а следовательно, для оперативного контроля такие способы не подходят.

Схема измерения радиуса кривизны волнового фронта представлена в статье. С помощью такого способа использования ДВФ появляется возможность не только измерения расстояния до центра источника сферического волнового фронта, но и измерения радиуса кривизны оптических деталей [9].

Сравнение различных методов измерения радиусов кривизн зеркал по точности и трудоемкости приведено в [7, 9].

Так как приборы с ДВФ имеют особенности определения центра кривизны волнового фронта [10], то вопрос точности совмещения луча лазерного дально- мера с этим центром требует более детального рассмотрения.

Учитывая эти особенности прибора с ДВФ, в статье анализируются погрешности измерения расстояний (радиуса кривизны волнового фронта и оптической детали) с использованием лазерного дальномера при неколлинеарном расположении измерительного канала.

В качестве высокоточного эталона расстояния при калибровке в приведенной схеме необходимо использовать зеркальную поверхность известного радиуса.

Таким образом, установив с помощью эталонного зеркала фиксированный радиус кривизны волнового фронта, приходящего на датчик Шака–Гартмана, можно, используя лазерный дальномер, определить его радиус.

1.    Описание способа измерения радиуса кривизны лазерным дальномером

Упрощенная схема прибора для измерения радиуса сферического зеркала с помощью лазерного дальномера [9] представлена на рис. 1. Оптическая ось дальномера 1 перпендикулярна оси измеряемого зеркала 4. Для направления луча на сферическое зеркало используется плоское зеркало 3, которое устанавливается таким образом, чтобы луч лазерного дальномера проходил через центр кривизны зеркала.

Определение положения центра кривизны измеряемого зеркала осуществляется с помощью прибора с датчиком волнового фронта, подробнее это будет описано в следующем параграфе. На рис. 1 приведена только необходимая для иллюстрации принципа измерения часть прибора с ДВФ – фокусирующая насадка 2, фокус которой должен быть совмещен с центром кривизны зеркала. Это совмещение, соответствующее автоколлимационному ходу лучей, контролируется с помощью ДВФ.

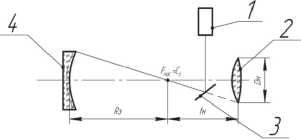
Рис. 1. Схема прибора для измерения радиуса вогнутого сферического зеркала с помощью лазерного дальномера

Радиус зеркала можно определить, если из расстояния, определенного дальномером (рис. 1), вычесть расстояние от дальномера до центра кривизны зеркала 4. Чтобы вычислить последнее расстояние, можно воспользоваться эталонным зеркалом (с известным радиусом кривизны), что позволит оставить измерительную схему без изменений и без дополнительных элементов. Такая схема для удобства расчетов представлена на рис. 2, где эталонное зеркало отмечено номером 5.

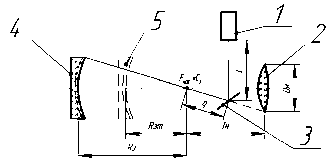
Рис. 2. Схема измерения с использованием эталонного зеркала

В этом случае сначала измеряется расстояние до эталонного зеркала, затем оно убирается и измеряется расстояние до исследуемого зеркала. Тогда радиус исследуемого зеркала рассчитывается по следующей формуле:

R з = D з - D эт + R эт,

где D з = L + q + R з – расстояние до исследуемого зеркала, измеренное дальномером; D эт = L + q + R эт – расстояние до эталонного зеркала, измеренное дальномером. В таком случае q и L отдельно не измеряются, значит, они никак не вносят погрешности, а погрешность определяется только погрешностью измерения R эт.

Однако в реальной системе возникает некоторая непредвиденная погрешность [10], выявленная на этапе юстировки, вклад которой в результат измерения и будет рассматриваться в данной работе.

2.    Схема начальной юстировки прибора

Как уже говорилось ранее, для измерения радиуса зеркала предложенным методом необходимо знать положение его центра кривизны. Для этого можно использовать собранный на кафедре РЛ2 прибор с датчиком волнового фронта, схема которого приведена на рис. 3.

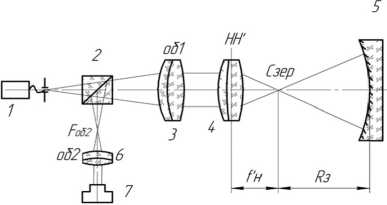
Рис. 3. Схема согласования центра кривизны исследуемого зеркала и фокуса насадки

Прибор включает в себя точечный источник излучения 1, формируемый полупроводниковым лазером с волоконным выходом, светоделительный куб 2, афокальную систему, состоящую из первого объектива 3 и второго объектива 6, фокусирующей насадки 4 и датчика волнового фронта 7. Измеряемой деталью является вогнутое сферическое зеркало 5. Источник излучения устанавливается в фокусе объектива 1, то есть волновой фронт после объектива 1 будет плоским. Далее излучение проходит через фокусирующую насадку, после чего оно будет сфокусировано в заднем фокусе насадки. Отраженное от зеркала излучение, пройдя через насадку, объектив 1 и частично отразившись светоделителем, попадает в передний фокус первого объектива 3. Пройдя второй объектив 6, излучение попадает на ДВФ. При совмещении центра кривизны зеркала с задним фокусом насадки формируется автоколлимационный ход лучей, контролируемый по плоскому волновому фронту, пришедшему на ДВФ. То есть зеркало, установленное на высокоточной подвижке, необходимо передвигать вдоль оси до тех пор, пока на ДВФ не будет зафиксирована гартманограмма, соответствующая плоскому волновому фронту.

3.    Причины возникновения погрешности

На самом деле экспериментально было установлено [7, 10], что плоский волновой фронт приходит на датчик не при идеальном совмещении центра кривизны зеркала и фокуса насадки, а при некотором их рассогласовании Δрасс, т.е. центр кривизны волнового фронта, пришедшего в прибор, не совпадает с фокусом насадки 4. На практике величину рассогласования с высокой точностью измерить и, как следствие, учесть невозможно, кроме того, для разных зеркал она не будет постоянной. Указанное рассогласование возникает вследствие следующих факторов:

• 1)    аберрационной каустики реальных оптических компонентов;

• 2)    каустики лазерного пучка (параметр конфокаль-ности);

• 3)    погрешности юстировки оптических компонентов (увеличивающей аберрационную каустику).

4.    Расчет погрешности

Если учитывать наличие такого рассогласования, использование формулы 1 для расчета радиуса кривизны зеркала будет давать большую погрешность. Чтобы ее определить и исключить, необходимо пересмотреть схему 1 с учетом наличия рассогласования (рис. 4).

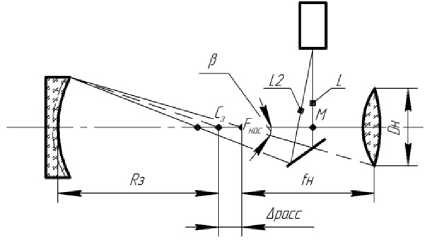
Рис. 4. Схема прибора с учетом рассогласования

Из схемы видно, что путь луча до исследуемого объекта и путь отраженного луча не совпадают. Для расчета погрешности необходимо рассчитать эти два расстояния и затем их разницу. Расстояния до зеркала L 1 и L 2 можно считать равными в силу их малости относительно расстояний от зеркала до объекта.

Для расчета путей лучей будем использовать следующие исходные данные:

• •    D н = 50 мм - диаметр фокусирующей насадки;

• •    /н = 500 мм - переднее фокусное расстояние насадки;

• •    R з = 1000.. .10000 мм - диапазон радиусов измеряемых зеркал;

• •    Арасс = 2.. .5 мм - диапазон возможных значений рассогласования.

Для удобства расчетов будет использована схема, представленная на рис. 5.

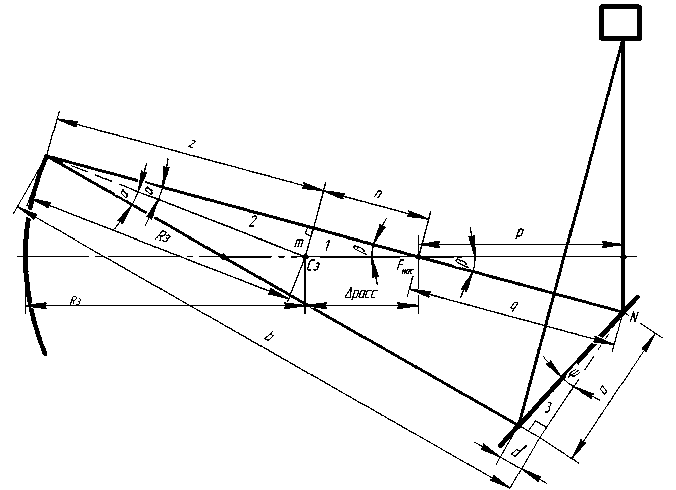
Рис. 5. Подробная схема для определения погрешности

Для определения путей лучей в первую очередь необходимо рассчитать угол между падающим и отраженным лучом 2α.

Отталкиваясь от известных данных, начнем расчет с определения угла β, который является апертурным углом фокусирующей насадки 4 (рис. 3).

tgр = (Dh /2) f н = 0,05 => р = 2,8°.(2)

Для расчетов проведем перпендикуляр из точки С з. Рассмотрим треугольник 1:

m = Арасс • sine = 0,048 • Арасс.(3)

Теперь рассмотрим треугольник 2.

n а = m / R з = ( 0,048 •Арасс) / R з.(4)

Остальные тригонометрические функции легко получить, используя основные формулы тригонометрии.

Путь луча до зеркала S 1 = L 1 + D 1, после отражения от зеркала S 2= D 2 + L 2.

Так как можем найти D 1 следующим образом:

D1 = q + n + z ,                                  (5)

где n = cos P•А расс = 0,998; •А расс, q = p /cos p =100,2мм, а p = 100 мм (из конструктивных соображений реального прибора), z =cos a • R з.

Проведем из точки N перпендикуляр к D 2, тогда D 2 = b - c . Причем b = D 1 • cos2 a , а для нахождения с рассмотрим треугольник 3:

tg v = c / a ,                                        (6)

где a = D1 • sin2a = D1 • 2sina • cosa,

V = (90 - 2 a ) - 46,4 = 43,6 - 2 a .

Из треугольника со сторонами p и q можно найти угол нормали к зеркалу в точке N как половину оставшегося угла этого треугольника (43,6 градуса). Тогда угол, дополняющий ψ до 90–2α, это будет угол 46,4 градуса.

Тогда получим следующее выражение для нахождения d :

d = ( ( 0,95 - tg2 a ) - a ) / ( 1 - 0,95tg2 a ) .            (7)

Погрешность будет определяться разностью путей падающего и отраженного лучей и будет зависеть от R з и Δрасс:

f ( Арасс, R з ) = D 1 - D 2 = q + n + z - b + d .       (8)

С помощью среды MathCad построено семейство графиков f (Δрасс) для 10 различных значений R з из заданного диапазона. Эти графики приведены на рис . 6.

Действительно, зависимость (8) имеет нелинейный вид, но если ограничить Δрасс до реально наблюдаемых величин (до 5 мм), то можно увидеть, что она практически линейна и одинакова для большого диапазона R з (рис. 7).

По графику можно сделать вывод, что в указанном диапазоне Δрасс и Rз погрешность, то есть разница между падающим и отраженными лучами, составляет 0,195…0,483 мм в зависимости от Δрасс и Rз. То есть для определения радиуса зеркал фор- мулой 1 необходимо учитывать наличие разности хода лучей.

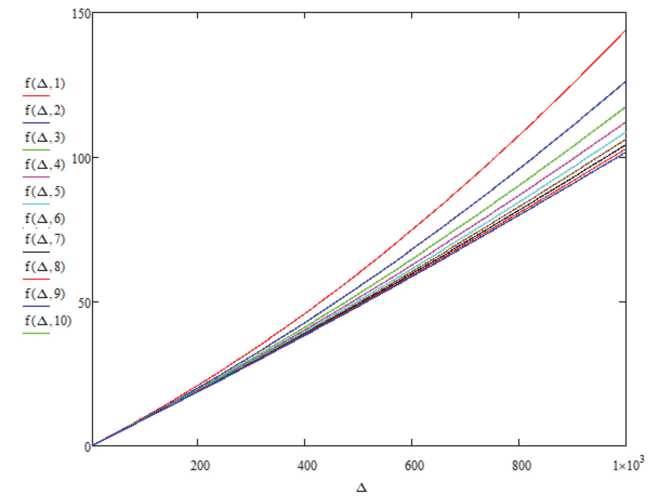
Рис. 6. График зависимости погрешности от Δрасс

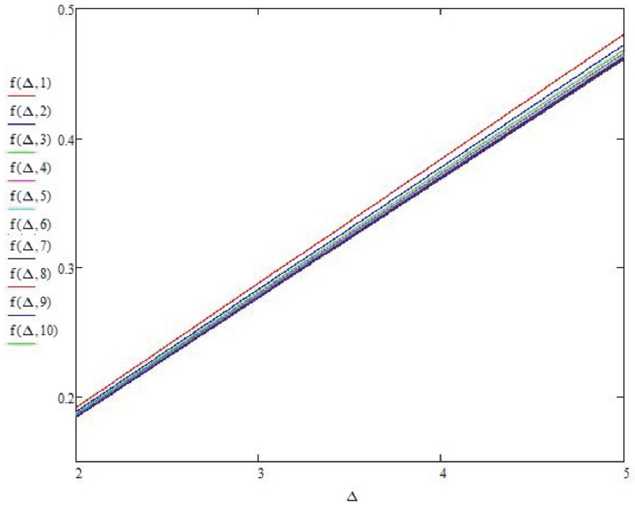
Рис. 7. График зависимости погрешности от Δрасс для заданного диапазона

Заключение

В ходе работы было определено, что использование лазерных дальномеров перспективно в развитии приборов определения параметров оптических поверхностей, в частности, для определения радиусов кривизны вогнутых сферических зеркал. Было показано, что при значительном [10] (до 5 мм) рассогласовании между фокусом насадки прибора с ДВФ и центром кривизны волнового фронта, приходящего в прибор, и диапазоне радиусов измеряемых зеркал от 1 до 10 м погрешность определения расстояния до зеркала не превышает 0,5 мм.

Подавляющее большинство представленных на современном рынке фазовых дальномеров (например, [11]) имеет погрешность определения расстояния не лучше 1 мм. При их использовании можно не учитывать погрешности юстировки прибора, и при расчетах вполне допустимо использовать формулу (1). В этом случае относительная погрешность определения радиуса кривизны составит 0,1 – 1 % для зеркал с указанными выше радиусами.

Современные научные разработки позволяют получить точность определения расстояния 0,2–0,3 мм для фазовых дальномеров, что в совокупности с высокоточными методами юстировки [9] снизит погрешность измерения радиусов кривизны зеркал до величины 0,02 – 0,3 %. Для зеркал, используемых в астрономических телескопах, радиус кривизны может достигать 50 м, а поскольку точность его измерения, как показано выше, полностью определяется погрешностью используемого дальномера, то относительная погрешность для этих зеркал может достигать 0,004 %.

Стоит отметить, что современные дальномеры [11] могут измерять дальность не только по зеркальному или световозвращающему объекту, но и по диффузно-отражающей поверхности, что существенно расширяет возможные области применения рассмотренного выше метода измерения радиусов оптических деталей. Так можно проводить измерения радиусов зеркал еще на стадии шлифования, что весьма актуально для зеркал астрономических телескопов, шлифование и полировка которых занимает большое количество времени. В самом деле, ИК-интерферометр или ИК-ДВФ [12] при использовании в схеме рис. 2 способны определить положение центра кривизны измеряемого зеркала, т.к. размер шероховатостей шлифованной поверхности заметно меньше их рабочей длины волны.

Еще одной областью применения дальномерного способа измерения радиуса кривизны зеркал можно считать измерение такового у оптических деталей с осевым отверстием, где прочие способы могут оказаться вовсе не работоспособными.

Таким образом, оценка влияния погрешностей юстировки, рассмотренных в работе, становится актуальной задачей.